Bölünen sayının en küçük en büyük olma durumları

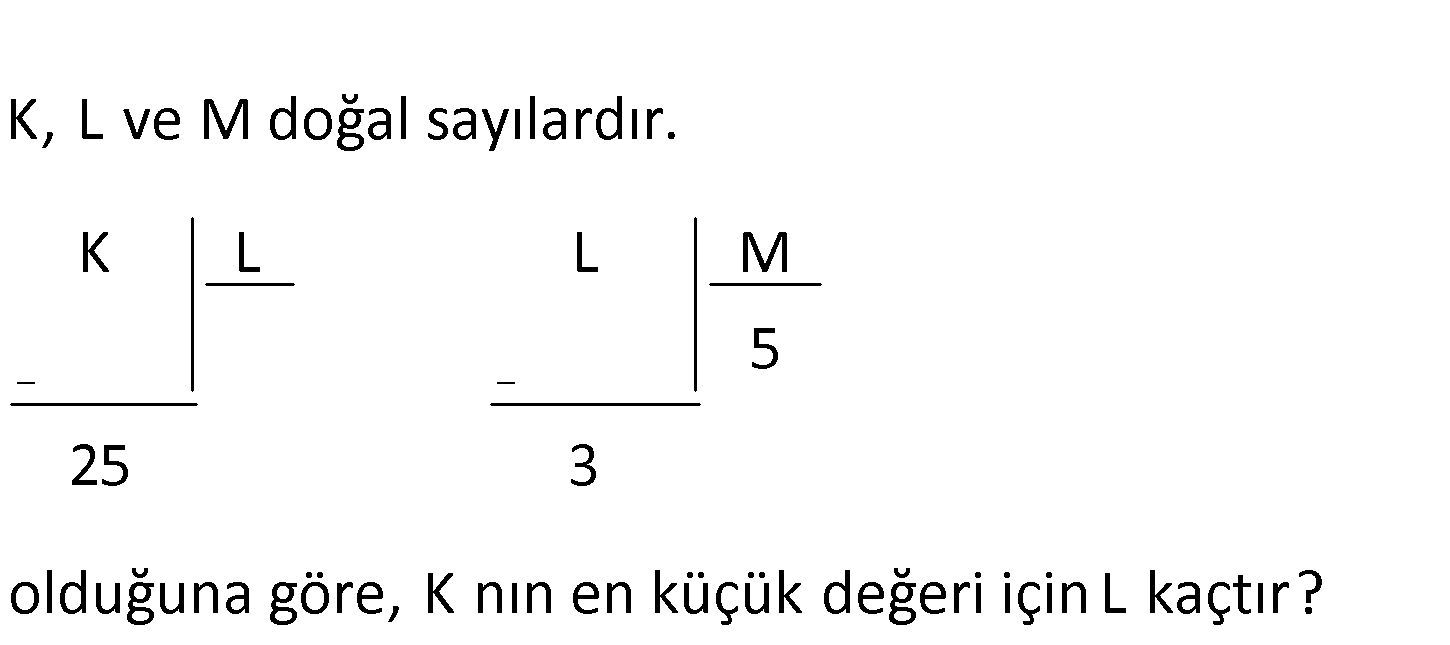
K, L ve M doğal sayılardır. K L L M 5 25   3 olduğuna göre, K nın en küçük değeri için L kaçtır? www.matematikkolay.net K L 25 Bir bölme işleminde bölen, kalandan büyük olmak zorundadır. L 25 K’nın : en k    Çözüm üçük olması için L ‘nin de olabildiğince en küçük seçilmesi gerekir. L M L 5M 3 dir. 5 3 L 25 idi 5M 3 25 5M 22 M en az 5 olabilir. L 5.5 3 28 buluruz            8
www.matematikkolay.net x ve y pozitif tam sayılardır. x 7 4 y  olduğuna göre, x en çok kaçtır? A) 32 B) 33 C) 34 D) 35 E) 36 Kalan, bölen sayıdan küçük olmak zorundadır. Bu sebeple y, en fazla 6 olabilir. Buna gö : re; x Çözüm  4.7 6  28  6  34 buluruz. 10
2 a ve b pozitif tam sayılardır. a b 3 12  olduğuna göre, a en az kaçtır? A) 39 B) 44 C) 52 D) 60 E) 64 2 Bölen sayı, kalandan büyük olmak zorundadır. b 12 ise b en az 4 olmalı ki karesi 12’den b :  ü Çözüm 2 yük olsun. a  3b 12  3.16 12  48 12  60 buluruz. www.matematikkolay.net 11
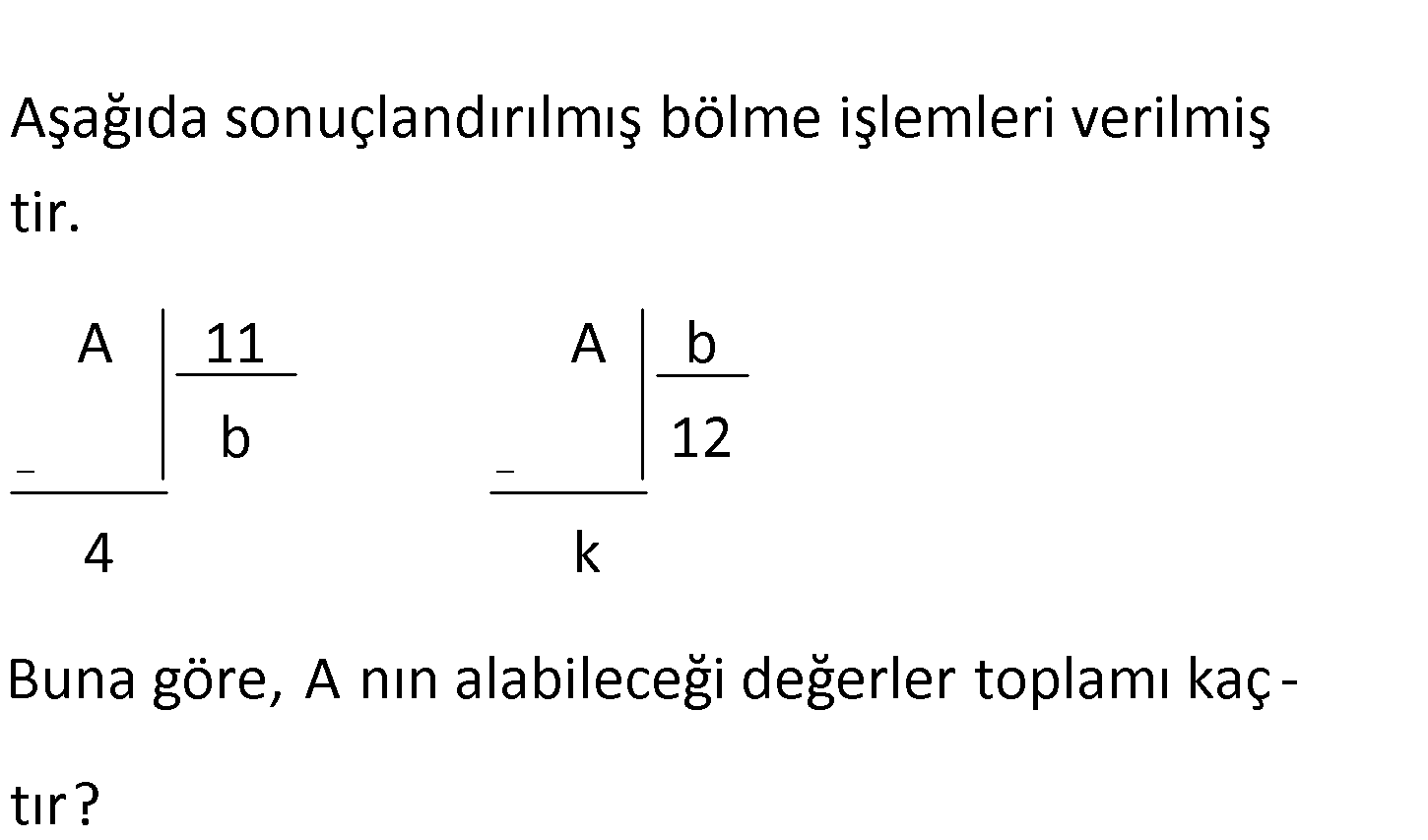
Aşağıda sonuçlandırılmış bölme işlemleri verilmiş A 11 A tir. b   b 12 4 k Buna göre, A nın alabileceği değerler toplamı kaç – tır? A 11b 4 (1.Bölme işlemine göre) A 12b k (2.Bölme işlemine göre) Bunları eş :     Çözüm itleyelim. 12b k 11b 4 b 4 k eşitliğini elde ederiz. k 0 için, b 4 A 11b 4 44 4 48 k 1 için, b 3 A 11b 4 33 4 37 k 2 için, b 2 (Bölüm, kalandan büyük olmalıdır. Bu sebeple kullanamayız.) k 3 iç                         in, b 1 Bunu da kullanamayız. A değerleri toplamı 48 37 85 buluruz.      www.matematikkolay.net 18
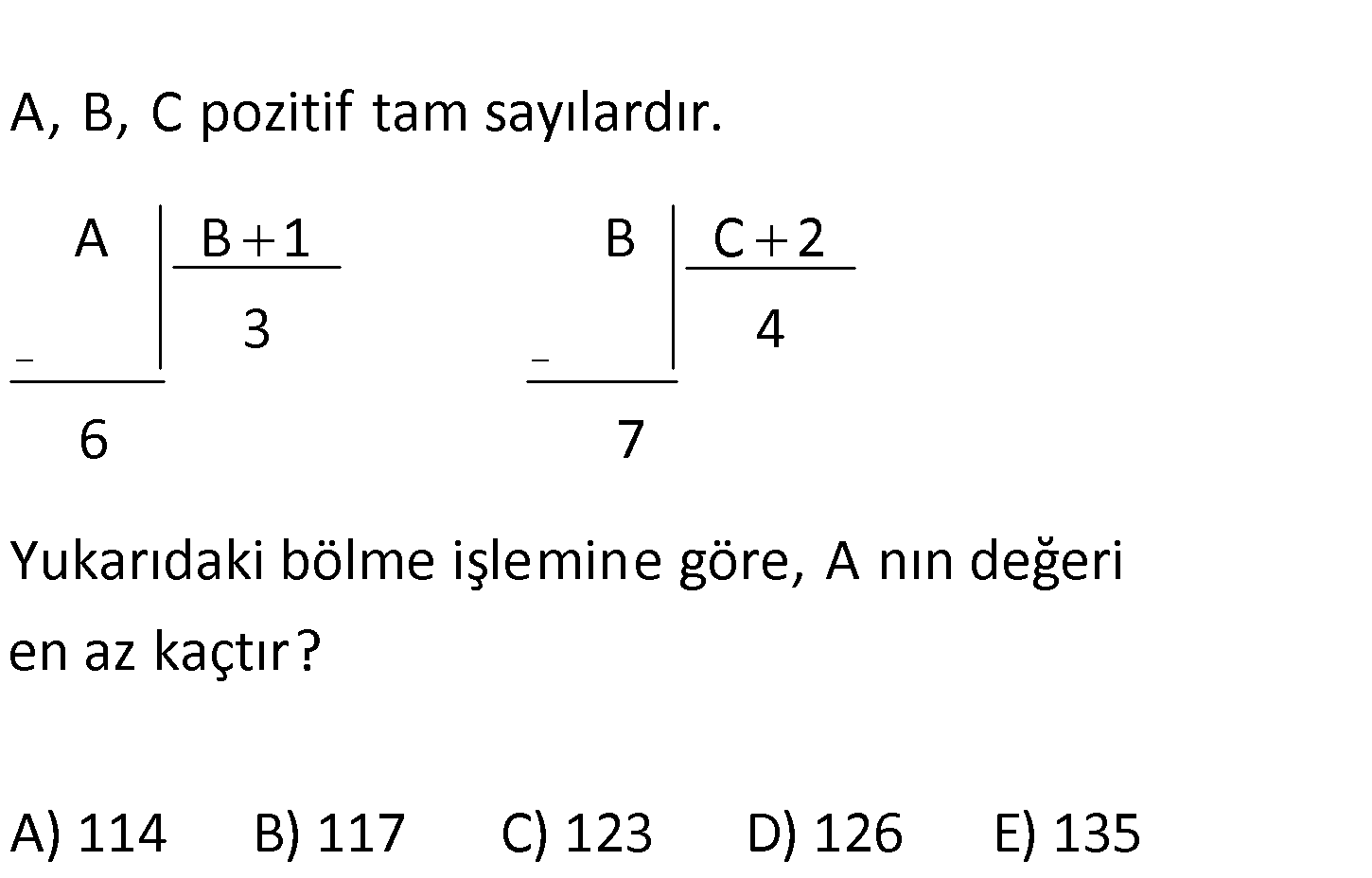
A B 1 B C 2 3 4 6 A, B, C pozitif tam sayılardır.     7 Yukarıdaki bölme işlemine göre, A nın değeri en az kaçtır? A) 114 B) 117 C) 123 D) 126 E) 135 www.matematikkolay.net Bölen sayı , kalandan büyük olmalıdır. Buna göre; C 2 7 C 5 tir. C en :      Çözüm         az 6 olabilir. O halde; B 4. C 2 7 4. 6 2 7 4.8 7 32 7 39 dur. (En küçük değeri) A 3 B 1 6 3. 39 1 6 3.40 6 120 6 126 buluruz.                       22
www.matematikkolay.net 2 m ve n pozitif tam sayılardır. m n n 2 9   Yukarıdaki sonuçlandırılmış bölme işlemine göre, m nin alabileceği en küçük değer kaçtır? A) 102 B) 103 C) 104 D) 105 E) 106     2 2 2 n 9 m n n 2 9 n, en az 4 olmalı. m 4 4 2 9 m 16.6 9 m 105 bulunur. :           Çözüm 42
www.matematikkolay.net 6x… 16 3… Olduğuna göre, x rakamının alabileceği değerler toplamı kaçtır? A) 3 B) 4 C)  5 D) 6 E) 8 6x… 16 3… 6x sayısının içinde yalnızca 3 kez 16 bulunmalıdır. x 0,1,2,3 olur :   Çözüm   . Ancak 4 olamaz. Çünkü 64 /16 4 tür. 3 değil artık Bu nedenle x 4 veya 4 ten büyük olamaz. x değerleri toplamı 0 1 2 3 6 buluruz.        63
A 6 n 1 n 2 A ve n birer doğal sayı ise A ‘nın alabileceği en bü – yük değer kaç    tır? www.matematikkolay.net Kalan sayı en az 0 olabilir. n 2 0 n 2 dir. O zaman; A 6 A 6.3 18 dir. 3 0 :        Çözüm  En küçük değeri 18 dir. 64