Soru Sor sayfası kullanılarak Olasılık konusu altında Olasılık denklemi, toplamı ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU (11.Sınıf)


4.SORU

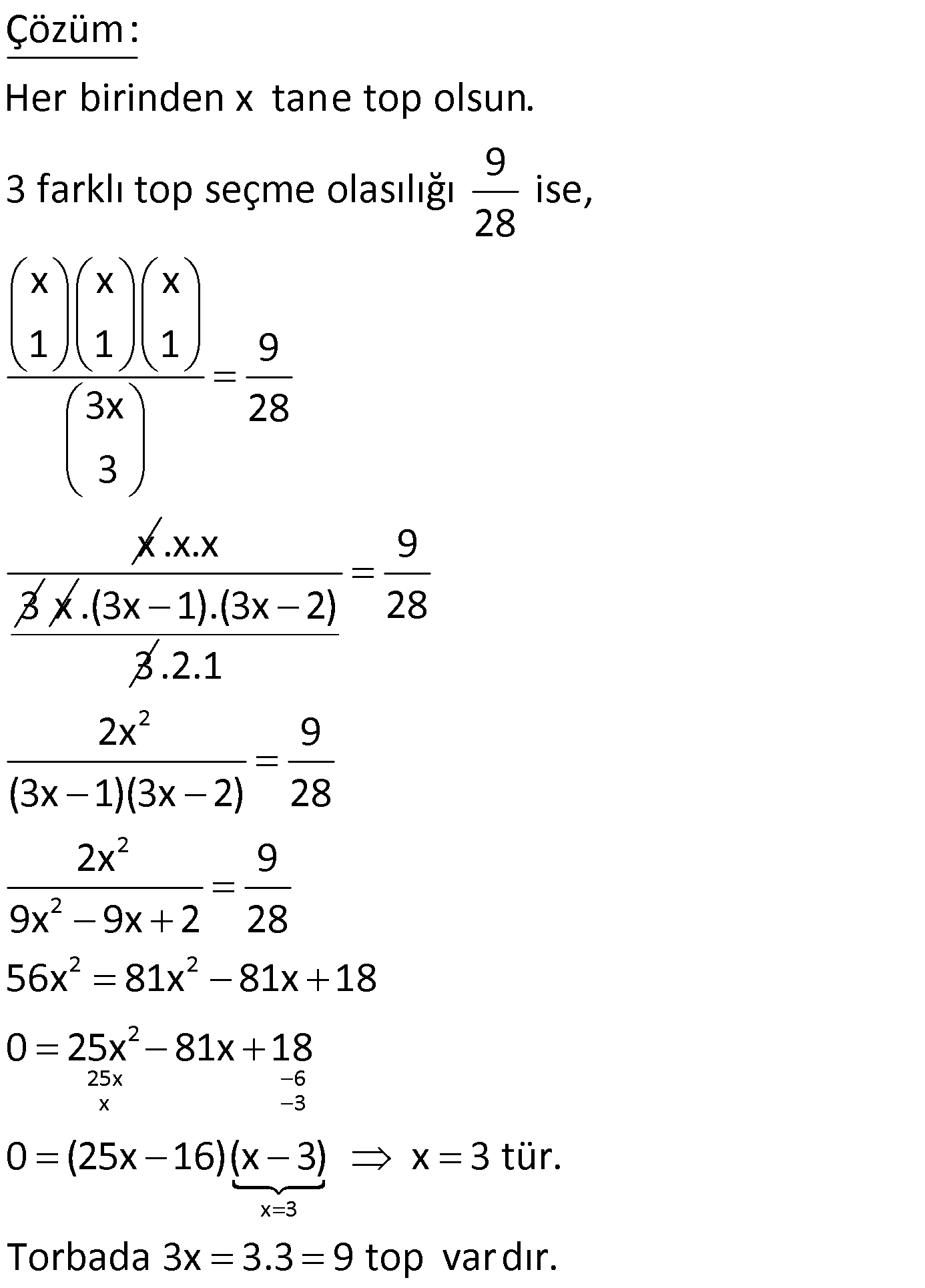
5.SORU (11.Sınıf)


6.SORU (11.Sınıf)


7.SORU


8.SORU (11.Sınıf)

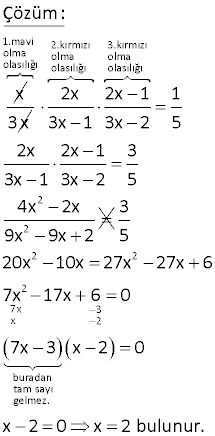
9.SORU (11.Sınıf)


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
x, y, z takımlarının katıldığı bir üçlü turnuvada x takımın kazanma olasılığı, y takımının kazanma olasılığının 3 katına, z takımının kazanma olasılığı – nın yarısına eşittir. Buna göre, y takımının turnuvayı kazanma olasılığı kaçtır? 1 1 1 1 1 A) B) C) D) E) 12 10 8 6 5 www.matematikkolay.net Çözüm: Tüm olasılıkların toplamı 1’e eşittir. P(x) P(y) P(z) 1 Soruda verilenlere göre olasılıklar arasında şöyle bir eşitlik var dır. 2P(x) 6P(y) P(z) 6k diyelim. Buna göre; P(x) 3k ; P(y) k ; P(z) 6k P(x) P(y) P(z) 1 ise 3k k 6k 1 1 10k 1 k dur. 10 1 P(y) k buluruz. 10 5 Ali, Melih ve Sinem’in katıldığı bir yarışta yarışı kazanma olasılıkları sırasıyla 2, 3 ve 5 ile orantılıdır. Buna göre, Sinem’in yarışı kazanma olasılığı kaçtır? 1 3 2 1 3 A) B) C) D) E) 5 10 5 2 5 www.matematikkolay.net Çözüm: Tüm olasılıkların toplamı 1’e eşittir. P(A) P(M) P(S) 1 Soruda verilenlere göre P(A) 2k ; P(M) 3k ; P(S) 5k dır. P(A) P(M) P(S) 1 ise 2k 3k 5k 1 1 10k 1 k dur. 10 5 1 P(S) 5k buluru 10 2 z. 6 Bir sınıftaki öğrencilerden her birinin bir sınavda 2 başarılı olma olasılığı tür. 3 Bu öğrencilerden 3 tanesi seçildiğinde, bu 3 öğren – ciden en az birinin sınavda başarılı olma olasılığı kaçtır? 26 A) 27 8 7 20 19 B) C) D) E) 9 9 27 27 www.matematikkolay.net Çözüm: Tüm olasılık tan, hepsinin başarısız olduğu durumu çıkararak soruyu çözebiliriz. 2 Bir öğrencinin başarılı olma olasılığı ise, başarısız 3 1 olma olasılığı tür. 3 Üç kişinin başarısız olma olaslılığı 1 1 1 1 dir. 3 3 3 27 Tüm durumdan çıkaralım. 1 26 1 buluruz. 27 27 35 Bir torbada eşit sayıda siyah, beyaz ve kırmızı top vardır. Çekilen top tekrar torbaya atılmaksızın art arda çekilen 3 topun üçünün de farklı renkte 9 gelme olasılığı ise torbada başlangıçta kaç 28 top vardır? www.matematikkolay.net 2 Çözüm: Her birinden x tane top olsun. İlk başta rastgele bir top çekilsin. 2x İkinci topun farklı renkte olma olasılığı dir. 3x 1 x Üçüncü topun ise dir. Buna göre; (3x 2) 2x x 9 1 ise; (3x 1) (3x 2) 28 2x 2 9 (3x 1)(3x 2) 28 x 9 x 3 tür. (3x 1)(3x 2) 56 Tüm toplar 3x 9 tanedir. 46 Ahmet’in sınavı kazanma olasılığı Veli’nin sınavı kazanma olasılığının 2 katıdır. 8 İkisinin birlikte sınavı kazanma olasılığı olduğuna 25 göre, yalnız birinin sınavı kazanma olasılığı kaçtır? 1 A) B 5 2 12 14 3 ) C) D) E) 5 25 25 5 www.matematikkolay.net 2 2 Veli Ahmet Veli Ahmet kazansın kazanmasın kazanmasın k Çözüm: Veli’nin kazanma olsaılığı p ise; Ahmet’inki 2p dir. 8 8 4 2 p.2p ise 2p p p tir. 25 25 25 5 Yalnız birinin kazanma olasılığı; 2 1 3 4 5 5 5 5 azansın 2 12 14 buluruz. 25 25 25 51 p(x) ve q(x) açık önermelerinin doğruluk kümeleri A ve B olmak üzere, U kümesinin elemanlarının % 60 ı A ve %25 i B kümesinin elemanıdır. Buna göre U kümesinden rastgele seçilecek bir eleman için, p q önermesinin doğru olma olasılığı yüzde kaçtır? A) 45 B) 55 C) 60 D) 65 E) 85 www.matematikkolay.net Çözüm: p q p’ q p’ nin olasılığı %(100 60) %40 q %25 p’ q %40 %25 %65 buluruz. 56 Beyaz ve kırmızı renkli kalemlerin bulunduğu bir kutudan rastgele bir kalem alındığında, kalemin 3 beyaz renkli olma olasılığı , rastgele iki kalem 8 alındığında kalemlerin farklı renklerde olma olası – lı 1 ğı olduğuna göre, bu kutudaki kalem sayısı 2 kaçtır? A) 8 B) 16 C) 24 D) 32 E) 40 www.matematikkolay.net Çözüm: Beyaz kalem sayısı b Kırmızı kalem sayısı k olsun. b 3 ise 8b 3b 3k b k 8 5b 3k dır. b 3x , k 5x diyebiliriz. İki kalem alındığında, kalemlerin farklı renk te olma olasılığı; 3x bk kb 8 x 5x 5 x 8x 1 8 x 3x 1 ise; 8x 1 2 15x 15x 1 64x 8 64x 8 2 30x 1 64x 8 60x 64x 8 2 4x 8 x 2 dir. Kutudaki kalem sayısı 3x 5x 8x 8.2 16 buluruz. 60 Ahmet, Mehmet ve Süreyya’nın yarıştığı üç kişilik bir yarışta yarışı Ahmet’in kazanma olasılığı Mehmet in kazanma olasılığının 2 katı, Süreyya’nın kazanma olasılığı Ahmet’in kazanma olasılığının 3 katıdır. Buna göre, yarışı Süreyya’nın kazanma olasılığı nedir? 2 1 1 1 1 A) B) C) D) E) 3 2 4 6 12 www.matematikkolay.net Çözüm: Mehmet’in kazanma olasılığı x olsun. Ahmet’in kazanma olasılığı 2x olur. Süreyya’nın kazanma olasılığı 6x olur. Tüm olasılıkların toplamı 1’dir. x 2x 6x 1 9x 1 1 x ‘dur. 9 Süreyya’nın kazanma olasılığı 6 2 6x bulunur. 9 3 61 Bir torbada x tane mavi, 2x tane kırmızı bilye vardır. Geri bırakılmadan (iadesiz) art arda alınan üç bilye – nin birincisin mavi, diğer ikisinin kırmız olma olası – 1 lığı olduğuna göre, x kaçtır ? 5 A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net Çözüm: x 3x 1.mavi 2.kırmızı 3.kırmızı olma olma olma olasılığı olasılığı olasılığı 2 2 2x 2x 1 1 3x 1 3x 2 5 2x 2x 1 3 3x 1 3x 2 5 4x 2x 9x 9x 2 2 2 2 7x 3 x 2 buradan tam sayı gelmez. 3 5 20x 10x 27x 27x 6 7x 17x 6 0 7x 3 x 2 0 x 2 0 x 2 bulunur. www.matematikkolay.net İki torbadan birincisinde 4 beyaz, 6 siyah; ikincisinde 2 beyaz ve bir miktar siyah top vardır. Birinci torbadan bir top çekilip rengine bakılmadan ikinci torbaya atılıyor. Daha sonra ikinci torbadan rastgele bir top çekil – 3 diğinde bunun beyaz olma olasılığı ise ikinci 10 torbadaki siyah top sayısı kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 Çözüm: İkinci torbada x sayıda siyah top olsun. Olasılık hesabında iki durumu dikkate alacağız. 1.Durum: İlk torbadan beyaz top çekildiğinde; diğer torbada beyaz sayısı 1 artacaktır. Buna göre 4 olasılık 10 3 olacaktır. x 3 2.Durum: İlk torbadan siyah top çekildiğinde; diğer torbada beyaz sayısı değişmeyecektir. Buna göre 6 2 olasılık olacaktır. 10 x 3 4 3 6 2 3 Toplam dur. 10 x 3 10 x 3 10 12 12 10 3 (x 3) 10 24 3 x 3 x 3 8 x 5 buluruz. www.matematikkolay.net 21

