
Yani, gidilen yolu bulmak için hız ile zaman çarpılır.
Örnek:
Bir otobüs, saatte 90 km hızla 450 km’lik yolu kaç saatte gider?
Çözüm:

Örnek:
Alican, yürüyerek 25 dakikada okuluna gitmektedir. Hızını 15 m/dk artırırsa okula 5 dakika daha erken varmaktadır. Alican’ın okulu kaç kilometre uzaktadır?
Çözüm:

Not: Hareket problemlerinde birimler arası çeviri yapmak gerekebilir.
1 km=1000 metredir.
1 saat=60 dakika
1 dakika=60 saniyedir.
Örnek:
12 km/saat kaç m/dk dır?
Çözüm:
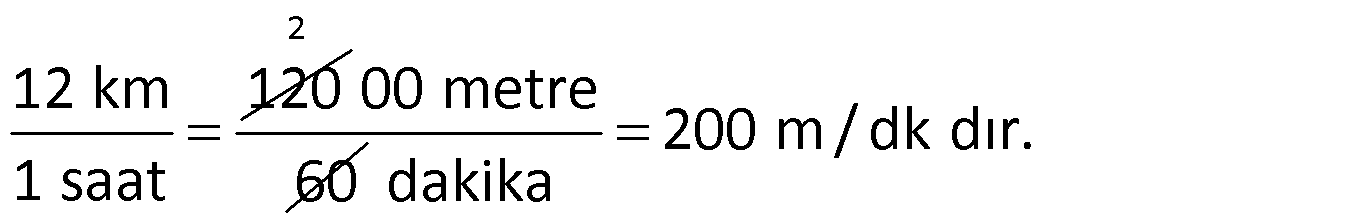
Örnek:
3 m/sn kaç km/sa dır?
Çözüm:
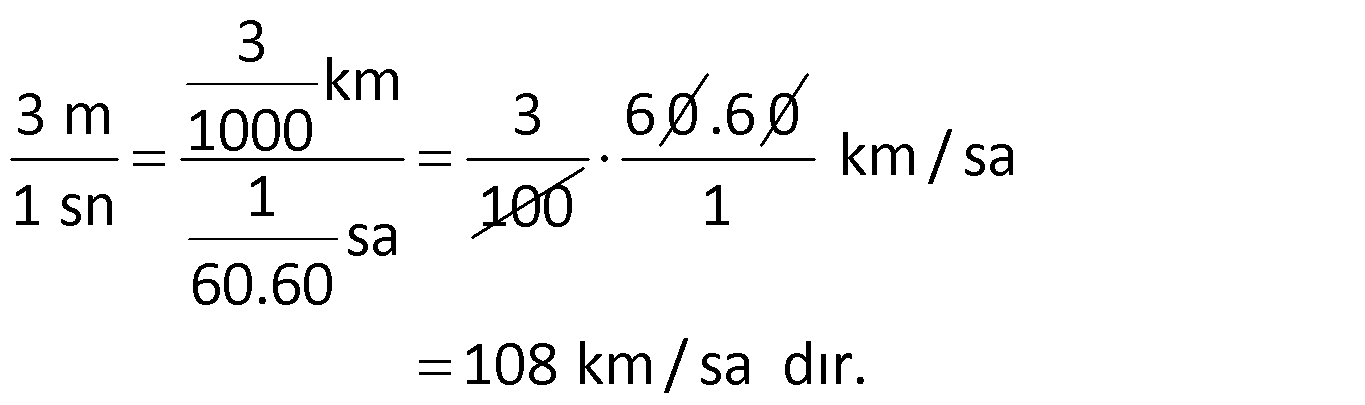
Örnek:
70 km’lik yolun 60 km’si şehirlerarası yol, 10 km’si şehir içi yoldur. Şehirlerarası hız sınırı 120 km/sa olup bir otomobil bu yolu en çabuk 42 dakikada tamamlayabilmektedir. Buna göre, şehir içi hız sınırı kaç km/sa tir?
Çözüm:

Ortalama Hız
Toplam yolu, toplam zamana bölersek ortalama hızı buluruz.

Örnek:
Bir araç, 200 km lik yolun 90 km’sini 60 km/sa hızla, geri kalanını ise 110 km/sa hızla gitmiştir. Buna göre, ortalama hız kaç km/sa tir?
Çözüm:
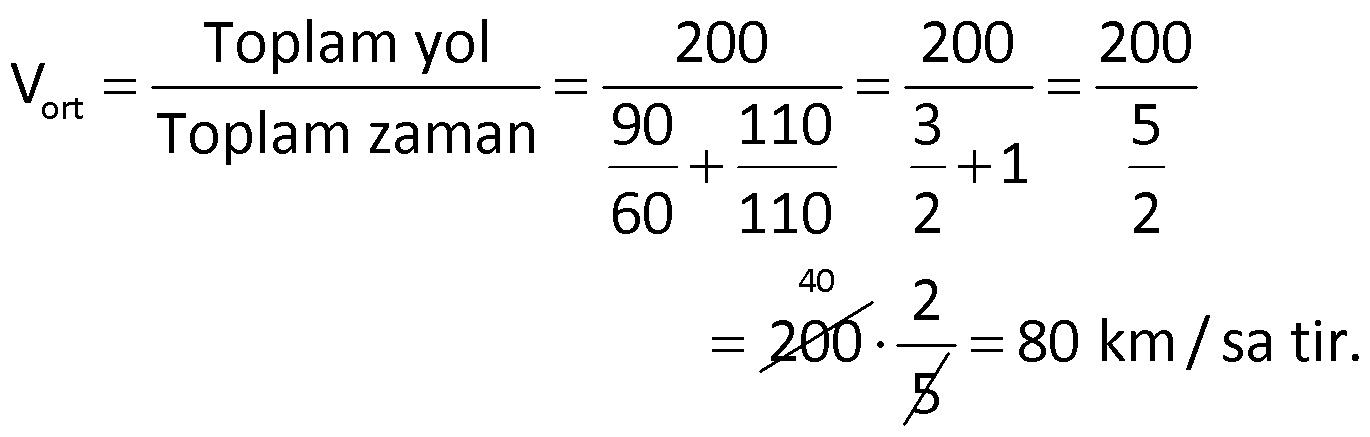
Not: Hızların aritmetik ortalaması ile ortalama hız aynı şey değildir. Her zaman toplam yol ve toplam zaman düşünülerek hesap yapılmalıdır. Sadece zamanlar eşit olduğunda aritmetik ortalama alabiliriz.
Örnek:
Bir araç, 60 km/sa ile gittiği yolu 90 km/sa ile geri dönmektedir. Ortalama hız kaç km/sa tir?
Çözüm:
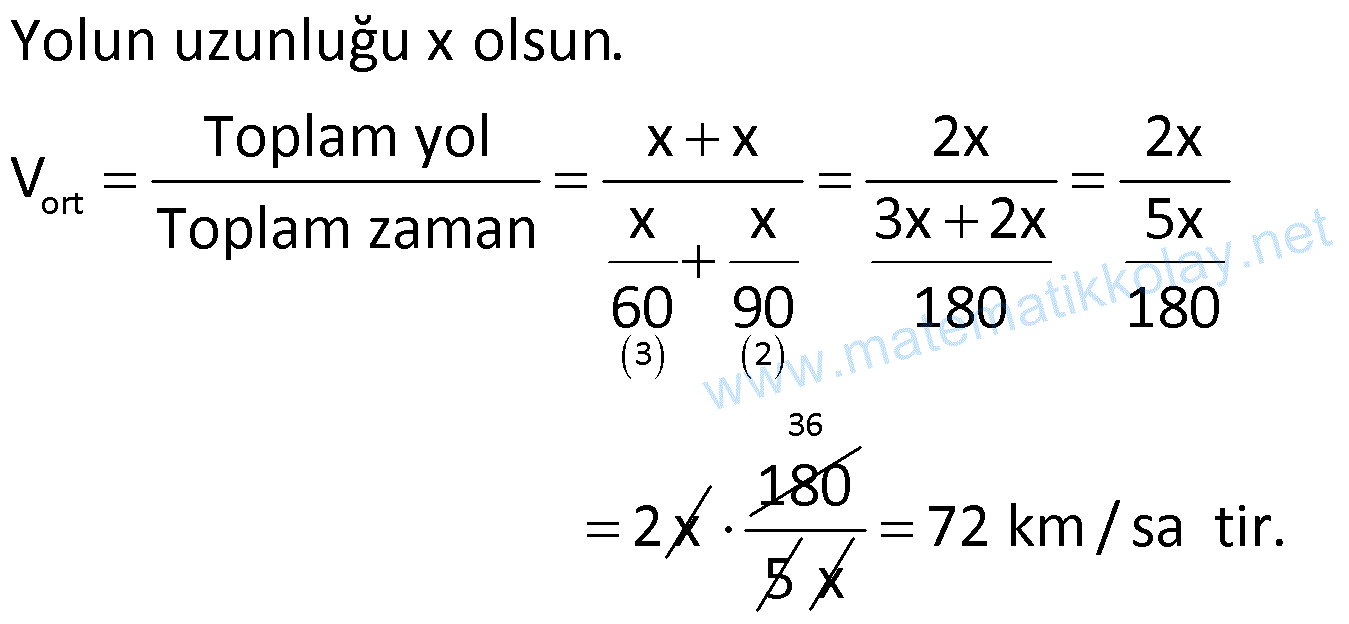
İki hareketlinin Birbirine Göre Durumları
1) Birbirlerine doğru hareket ederlerse, hızları toplamı kadar birbirine yaklaşırlar.
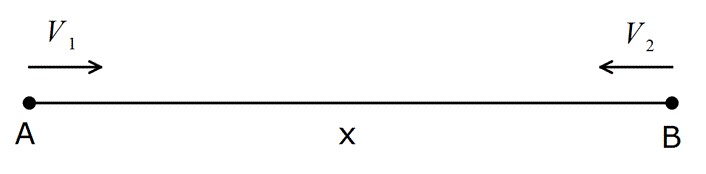
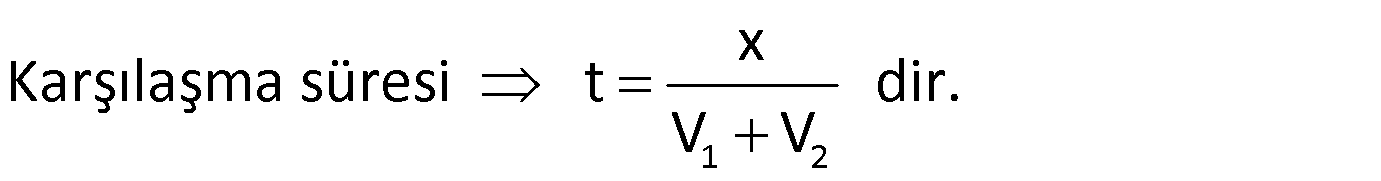
Örnek:
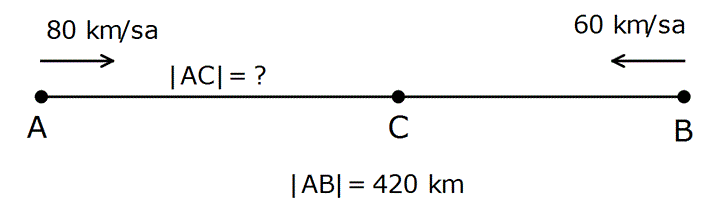
Yukarıdaki şekilde iki hareketli C noktasında karşılaşıyorlar. A-C arası mesafe kaç km dir?
Çözüm:

2) Arkadan gelen araç yetişmeye çalıştığında, hızının farkı kadar yaklaşır.
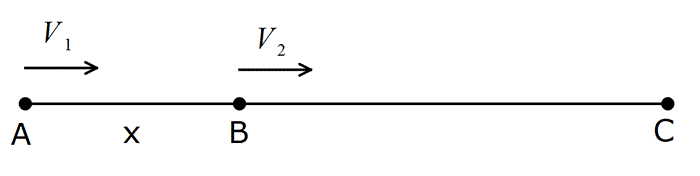
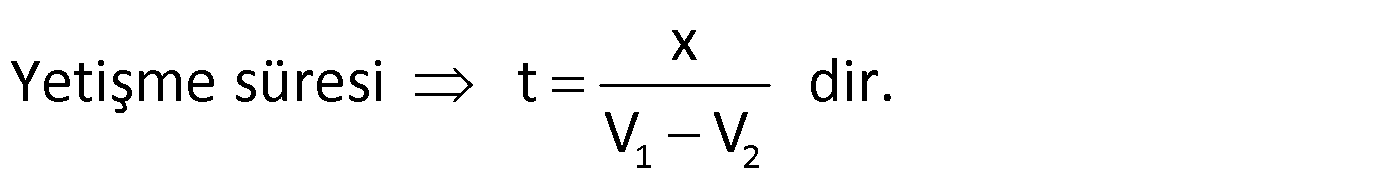
Örnek:
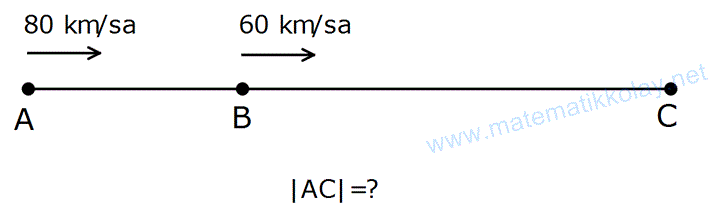
Yukarıdaki şekilde, A’daki araç, B’deki aracı 5 saat sonra C noktasında yakalıyor. Buna göre, |AB| arası mesafe kaç km dir?
Çözüm:
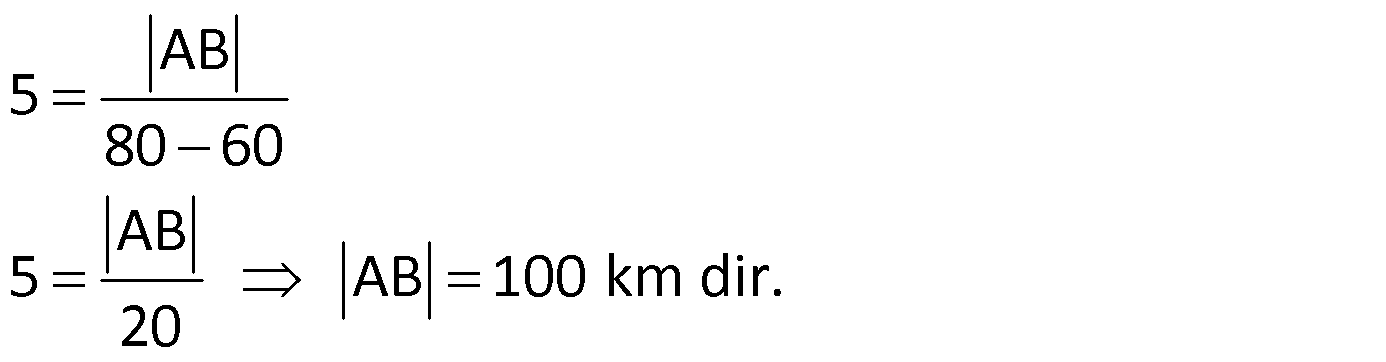
Örnek:
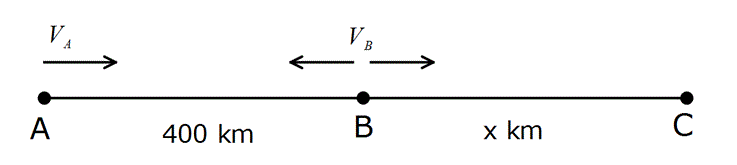
Yukarıdaki iki araç birbirlerine doğru hareket ederlerse 2 saatte karşılaşıyorlar. Eğer ikisi de C’ye doğru giderse A’daki araç, B’deki aracı C noktasında 10 saat sonra yakalıyor. Buna göre, |BC| arası mesafe kaç km dir?
Çözüm:
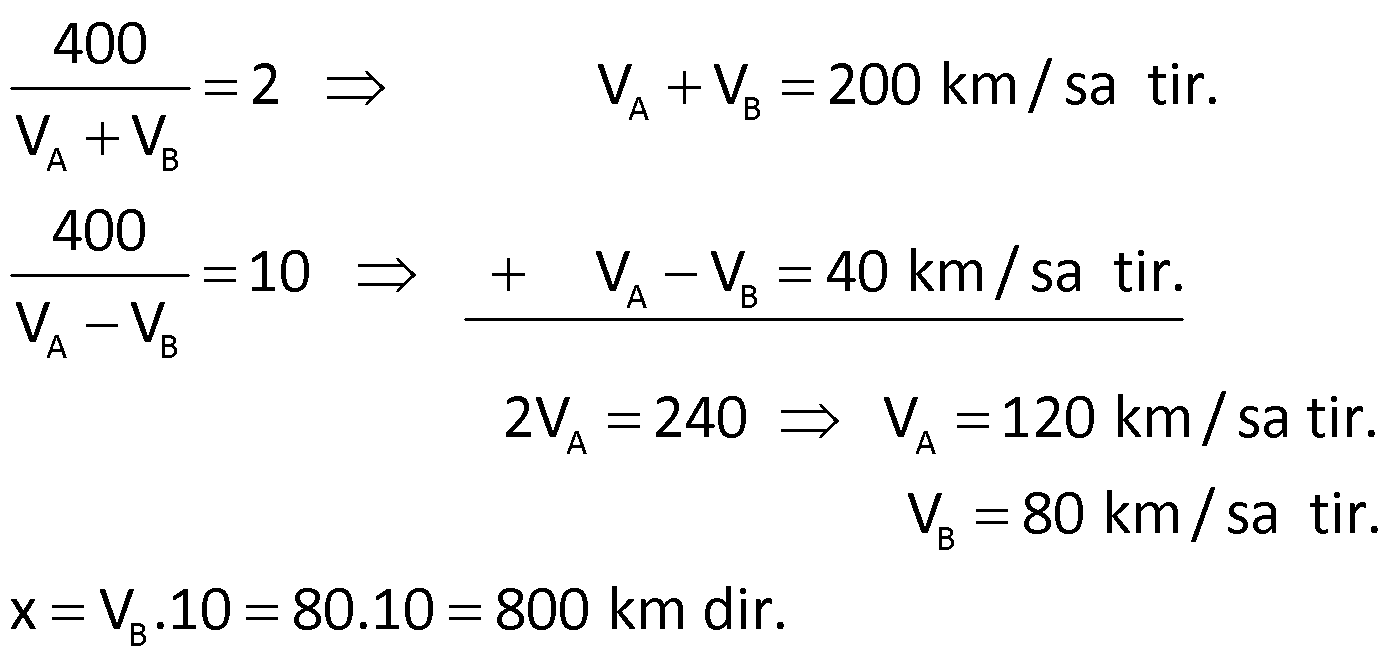
Örnek:
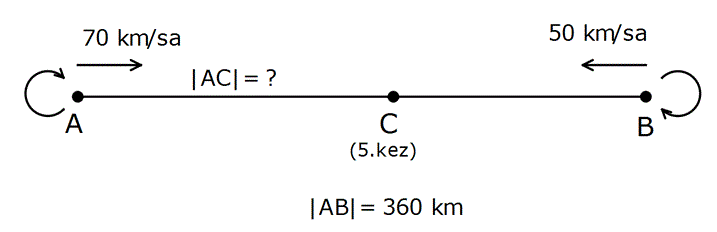
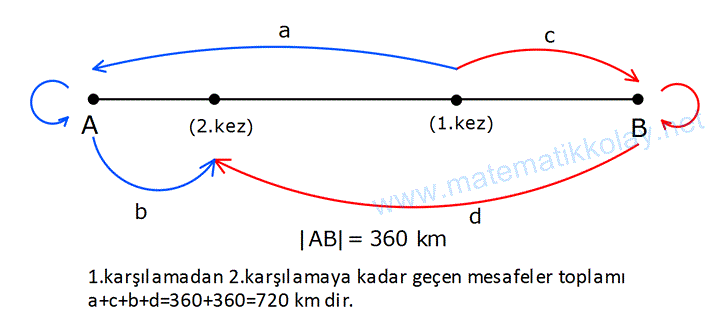
Yukarıdaki iki araç birbirlerine doğru hareket ediyor. En uçtaki noktaya ulaştıktan sonra geri dönüp hareketlerine devam ediyorlar. 5.kez karşılaştıkları nokta A’dan kaç km uzaktadır?
Çözüm:
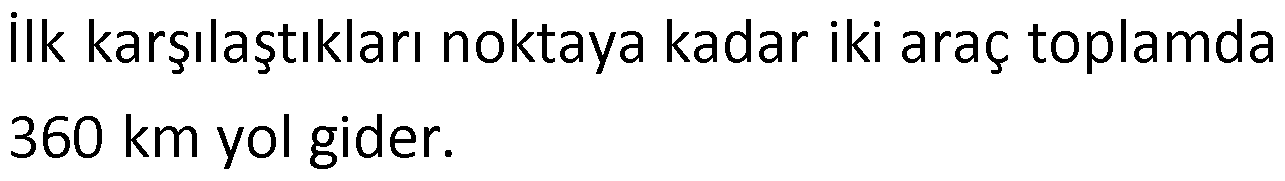

Örnek:
Bir koşu pistte 1.atlet yarışı 2. atletten 36 metre önde, 3.atletten 72 metre önde bitirmektedir. 2.atlet ise 3.atletten 40 metre önde bitirmektedir. Buna göre, pistin uzunluğu kaç metredir?
Çözüm:

3) Dairesel pistte zıt yönlü hareketliler, hızları toplamı kadar birbirlerine yaklaşırlar.
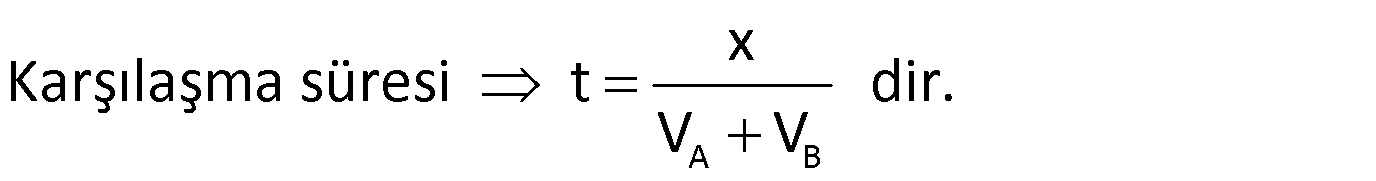
Örnek:
Dairesel bir pistte hızları 20 m/dk ve 30 m/dk olan iki araç, aynı noktadan zıt yönlü olarak hareket etmektedir. Bu iki araç 20 dakika sonra 2.kez karşılaştıklarına göre, pistin çevresi kaç metredir.
Çözüm:

4) Dairesel pistte aynı yönlü harekette, iki araç arasında tam bir pist mesafesi varmış gibi düşünülmelidir. Hızlı olan araç hız farkıyla bir pist mesafesini bitirirse, yavaş olanı yakalar.
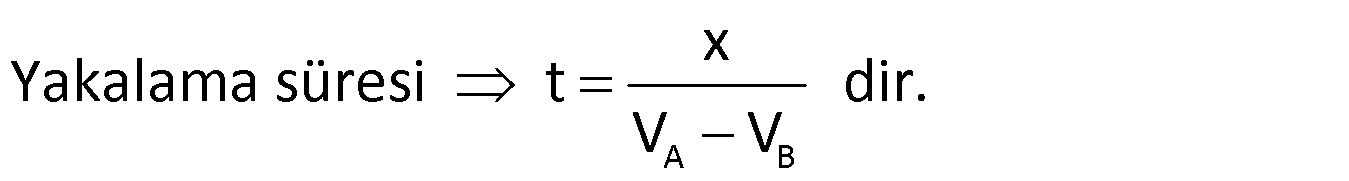
Örnek:
280 metre uzunluğundaki dairesel bir pistte iki araç aynı noktadan aynı yöne doğru hareket ettiklerinde hızlı olan araç yavaş olanı 14 dakikada yakalıyor. Eğer zıt yönde hareket ederlerse 2 dakikada karşılaşıyorlar. Hızlı olan aracın hızı kaç m/dk dır?
Çözüm:
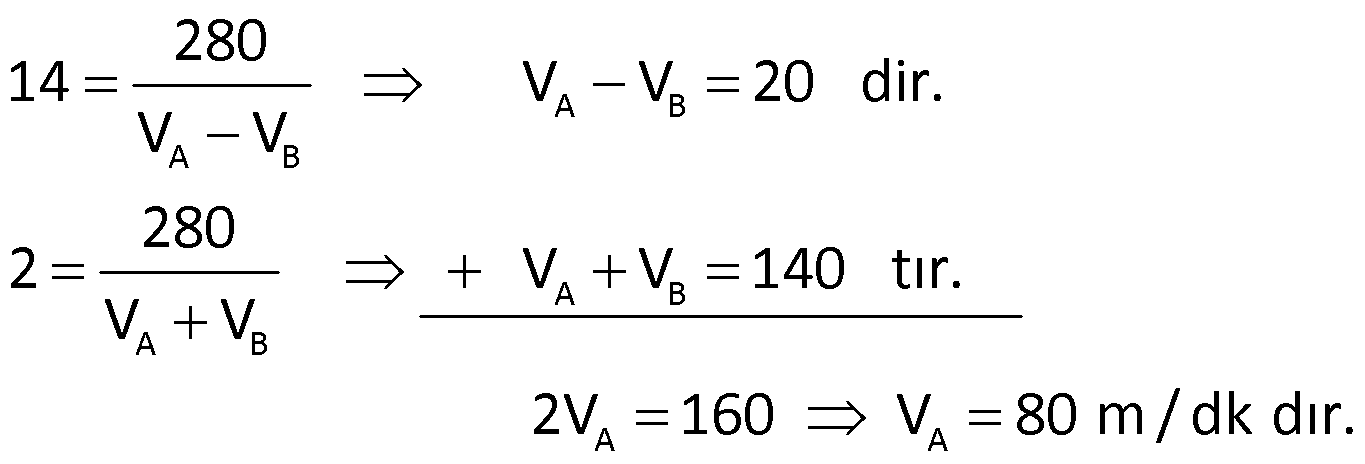
Örnek:
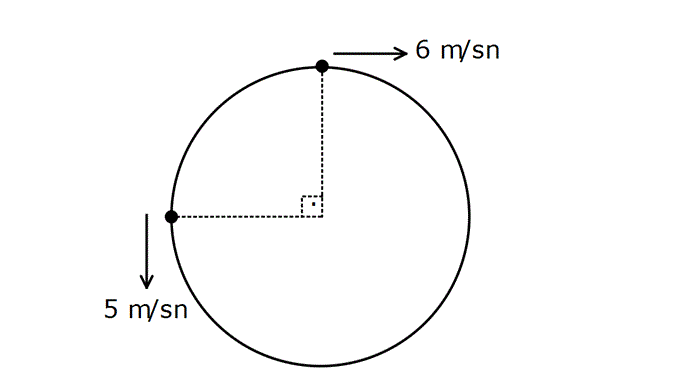
Yukarıdaki iki hareketli 14 saniye sonra 2.defa karşılaştıklarına göre, pistin çevresi kaç metredir?
Çözüm:

Örnek:
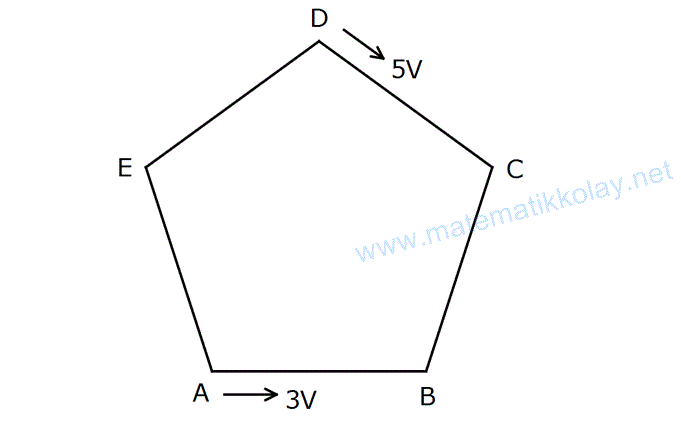
Yukarıdaki düzgün beşgen şeklindeki bir pistte iki hareketli sürekli olarak karşılaşmaktadırlar. 10.kez hangi noktada karşılaşırlar?
Çözüm:

Örnek:
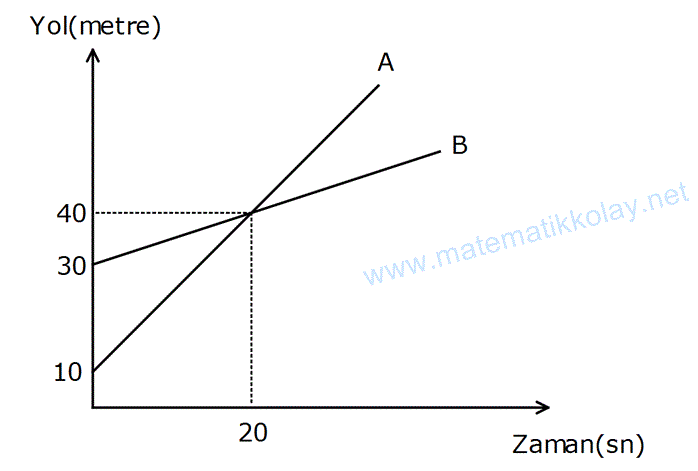
Yukarıdaki yol zaman grafiğe, iki araç aynı konuma geldikten 30 saniye sonra aralarındaki mesafe kaç metre olur?
Çözüm:

Örnek:
Durgun sudaki hızı 25 m/dk olan bir teknenin, akıntı hızı 5 m/dk olan bir nehirde gidip, başladığı noktaya geri dönecektir. Tüm yolculuğu 20 dakika sürdüğüne bu tekne en fazla kaç metre uzağa gidebilmiştir?
Çözüm:

Örnek:
150 metre uzunluğundaki bir tren 250 m’lik bir tüneli 20 saniyede geçiyor. Buna göre, trenin hızı kaç km/sa tir?
Çözüm:


Örnek:

Çözüm:

Örnek:
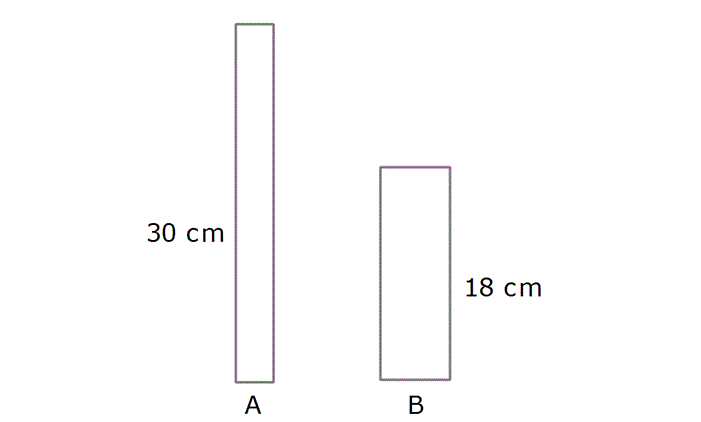

Çözüm:

Çözümlü Sorular veya Daha Fazlası için Tıkla
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
HAREKET PROBLEMLERİ KONU ANLATIMI www.matematikkolay.net Yol x Hız V şeklinde gösterilir ve x V.t dir. Zaman t Yani, gidilen yolu bulmak için hız ile zaman çarpılır. Örnek: Bir otobüs, saatte 90 km hızla 450 km’lik yolu kaç saatte gider? Çözüm: x V.t 450 5 90.t t 5 saatte gider. Örnek: Alican, yürüyerek 25 dakikada okuluna gitmektedir. Hızını 15 m/dk artırırsa okula 5 dakika daha erken varmaktadır. Alican’ın okulu kaç kilometre uzaktadır? Çözüm: İlk hızına V m / dk diyelim. 25 dakikada, x 25V metre gider. Hızını V 15 yapınca 20 dakikada gidiyorsa, x (V 15).20 metredir. İkisini birbirine eşitleyelim. 25V (V 15).20 25V 20V 300 5V 300 V 60 m/ dk dır. x 2 5V idi. 25.60 1500 metre 1,5 km dir. Not: Hareket problemlerinde birimler arası çeviri yapmak gerekebilir. 1 km=1000 metredir. 1 saat=60 dakika 1 dakika=60 saniyedir. Örnek: 12 km/saat kaç m/dk dır? Çözüm: 12 km 120 1 saat 2 00 metre 60 200 m/ dk dır. dakika Örnek: 3 m/sn kaç km/sa dır? Çözüm: 3 km 3 m 1000 3 1 sn 1 100 sa 60.60 6 0 .6 0 km/ sa 1 108 km/ sa dır. Örnek: 70 km’lik yolun 60 km’si şehirlerarası yol, 10 km’si şehir içi yoldur. Şehirlerarası hız sınırı 120 km/sa olup bir otomobil bu yolu en çabuk 42 dakikada tamamlayabilmektedir. Buna göre, şehir içi hız sınırı kaç km/sa tir? Çözüm: 60 1 Şehirlererarası 60 km’lik yol saatte 120 2 1 biter. saat 30 dakikadır. 2 Geriye 42 30 12 dakika kalır. 12 1 12 dakika saat saattir. 60 5 1 10 km lik yol saatte tamamlanıyorsa 5 10 1 V 50 km/ sa V 5 hız sınırı var dır. Ortalama Hız Toplam yolu, toplam zamana bölersek ortalama hızı buluruz. ort Toplam yol V Toplam zaman Örnek: Bir araç, 200 km lik yolun 90 km’sini 60 km/sa hızla, geri kalanını ise 110 km/sa hızla gitmiştir. Buna göre, ortalama hız kaç km/sa tir? Çözüm: ort Toplam yol 200 200 200 V Toplam zaman 90 110 3 5 1 60 110 2 2 200 40 2 5 80 km/ sa tir. www.matematikkolay.net Not: Hızların aritmetik ortalaması ile ortalama hız aynı şey değildir. Her zaman toplam yol ve toplam zaman düşünülerek hesap yapılmalıdır. Sadece zamanlar eşit olduğunda aritmetik ortalama alabiliriz. Örnek: Bir araç, 60 km/sa ile gittiği yolu 90 km/sa ile geri dönmektedir. Ortalama hız kaç km/sa tir? Çözüm: ort 3 2 Yolun uzunluğu x olsun. Toplam yol x x 2x 2x V Toplam zaman x x 3x 2x 5x 60 90 180 180 2 x 180 36 5 x 72 km/ sa tir. İki hareketlinin Birbirine Göre Durumları 1) Birbirlerine doğru hareket ederlerse, hızları toplamı kadar birbirine yaklaşırlar. 1 2 x Karşılaşma süresi t dir. V V Örnek: Yukarıdaki şekilde iki hareketli C noktasında karşılaşıyorlar. A-C arası mesafe kaç km dir? Çözüm: 420 420 3 saat sonra karşılaşırlar. 80 60 140 A’dan çıkan araç, 3 saat sonra C noktasına varmıştır. AC 80.3 240 km dir. 2) Arkadan gelen araç yetişmeye çalıştığında, hızının farkı kadar yaklaşır. 1 2 x Yetişme süresi t dir. V V Örnek: Yukarıdaki şekilde, A’daki araç, B’deki aracı 5 saat sonra C noktasında yakalıyor. Buna göre, |AB| arası mesafe kaç km dir? Çözüm: AB 5 80 60 AB 5 AB 100 km dir. 20 Örnek: Yukarıdaki iki araç birbirlerine doğru hareket ederlerse 2 saatte karşılaşıyorlar. Eğer ikisi de C’ye doğru giderse A’daki araç, B’deki aracı C noktasında 10 saat sonra yakalıyor. Buna göre, |BC| arası mesafe kaç km dir? Çözüm: A B A B A B A B A A 400 2 V V 200 km/ sa tir. V V 400 10 V V 40 km/ sa tir. V V 2V 240 V 120 km/ sa tir. B B V 80 km/ sa tir. x V .10 80.10 800 km dir. Örnek: www.matematikkolay.net Yukarıdaki iki araç birbirlerine doğru hareket ediyor. En uçtaki noktaya ulaştıktan sonra geri dönüp hareketlerine devam ediyorlar. 5.kez karşılaştıkları nokta A’dan kaç km uzaktadır? Çözüm: İlk karşılaştıkları noktaya kadar iki araç toplamda 360 km yol gider. Karşılaştıkları noktadan gidip geri dönünce tekrar karşılaşana kadar iki araç toplamda 720 km yol gider. Bundan sonra her karşılaşma için 720 km yol giderler. O halde, 5.kez karşılaşıncaya kadar, toplamda 360 4.720 4 2880 3240 km yol giderler. Hızları toplamı 120 km / sa olduğuna göre, 3240 27 saat sonra 5.kez karşılaşmış olurlar. 120 A’daki araç 27 saatte 1890 km yol gider. Her 360 360 720 km’de başa dö ner. 1890’un 720 ile bölümünden kalan 450 km dir. 1890 2.720 450 O halde, A’dan 450 km gidelim. 360 km sonrası B’dir. 90 km de geriye dönünce A’ya 270 km kalır. O halde, AC 270 km dir. Örnek: Bir koşu pistte 1.atlet yarışı 2. atletten 36 metre önde, 3.atletten 72 metre önde bitirmektedir. 2.atlet ise 3.atletten 40 metre önde bitirmektedir. Buna göre, pistin uzunluğu kaç metredir? Çözüm: Pistin uzunluğuna x diyelim. 1.durumda 2.atlet x 36 metre koşarken, 3.atlet x 72 metre koşabilmiştir. Geçen süre, ikisi için de aynı olduğu için hızları oranı, gittikleri yolun oranı x 36 na eşittir. dir. x 72 1.durumdan 2.duruma kadar, 2.atlet 36 metre koşarken, 3.atlet 72 40 32 metre 36 koşabilmiştir. Hızları oranı dir. 32 Bu ikisini eşitleyelim. x 36 36 x 72 9 32 8 8x 288 9x 648 648 288 x 360 x tir. koşu pisti 360 metredir. 3) Dairesel pistte zıt yönlü hareketliler, hızları toplamı kadar birbirlerine yaklaşırlar. A B x Karşılaşma süresi t dir. V V Örnek: Dairesel bir pistte hızları 20 m/dk ve 30 m/dk olan iki araç, aynı noktadan zıt yönlü olarak hareket etmektedir. Bu iki araç 20 dakika sonra 2.kez karşılaştıklarına göre, pistin çevresi kaç metredir. Çözüm: www.matematikkolay.net Her karşılaşma için, toplamda pistin çevresi kadar yol gitmeleri gerekmektedir. 2.kez karşılaştıklarında 2x kadar yol gitmişlerdir. 2x 20 dakika ise, 20 30 2x 20 2x 1000 x 500 metredir. 50 4) Dairesel pistte aynı yönlü harekette, iki araç arasında tam bir pist mesafesi varmış gibi düşünülmelidir. Hızlı olan araç hız farkıyla bir pist mesafesini bitirirse, yavaş olanı yakalar. A B x Yakalama süresi t dir. V V Örnek: 280 metre uzunluğundaki dairesel bir pistte iki araç aynı noktadan aynı yöne doğru hareket ettiklerinde hızlı olan araç yavaş olanı 14 dakikada yakalıyor. Eğer zıt yönde hareket ederlerse 2 dakikada karşılaşıyorlar. Hızlı olan aracın hızı kaç m/dk dır? Çözüm: A B A B A B A B A A 280 14 V V 20 dir. V V 280 2 V V 140 tır. V V 2V 160 V 80 m/ dk dır. Örnek: Yukarıdaki iki hareketli 14 saniye sonra 2.defa karşılaştıklarına göre, pistin çevresi kaç metredir? Çözüm: Pistin çevresine 4x diyelim. İlk önce, birbirlerine doğru toplamda 3x mesafe gittiklerinde karşılaşırlar. Sonra tam bir pist mesafesi gittiklerinde karşılaşırlar. O halde 7x mesafe gittiklerinde 2.kez karşılaşırlar. 7x 14.(5 6) 7 x 14 2 .11 x 22 metre Pist 4x 4.22 88 metredir. Örnek: Yukarıdaki düzgün beşgen şeklindeki bir pistte iki hareketli sürekli olarak karşılaşmaktadırlar. 10.kez hangi noktada karşılaşırlar? Çözüm: www.matematikkolay.net Beşgenin bir kenarına x diyelim. İlk karşılaşmaları, toplamda 3x mesafe gittiklerinde gerçekleşir. Daha sonra hep 5x mesafe gittiklerinde karşılaşırlar. O halde, 10.kez karşılaşmaları için 3x 9.5x 3x 45x 48x mesafe gitmelilerdir. 48x 48x 6x Bunun için gerekli süre dir. 3V 5V 8V V Bu sürede A’dan yola çıkan araç, 3V 6x V 18x mesafe gitmiştir. Pistin çevresi 5x olduğuna göre, pisti 3 kez turlamış ve geriye 3x mesafe kalmıştır. A’dan sonra 3x mesafe gidersek D noktasına varırız. Cevap D noktası olur. Örnek: Yukarıdaki yol zaman grafiğe, iki araç aynı konuma geldikten 30 saniye sonra aralarındaki mesafe kaç metre olur? Çözüm: A B 40 10 30 3 V m/ sn dir. 20 20 2 40 30 10 1 V m/ sn dir. 20 20 2 Karşılaştık tan 30 saniye aradaki fark, 3 1 2 30 30 30.1 30 metre olur. 2 2 2 İki araç arasında başlangıçta 20 metr II.Yol : e fark vardır. 20 saniyede 20 metre fark kapanıyorsa 30 saniyede x metre fark açılır 30.20 x 20 30 metredir. Örnek: Durgun sudaki hızı 25 m/dk olan bir teknenin, akıntı hızı 5 m/dk olan bir nehirde gidip, başladığı noktaya geri dönecektir. Tüm yolculuğu 20 dakika sürdüğüne bu tekne en fazla kaç metre uzağa gidebilmiştir? Çözüm: Teknenin hızı akıntı ile beraber 25 5 30 m/ dk akıntıya karşı 25 5 20 m/ dk dır. 30 m/ dk ile t dakika gitmiş olsun. 20 m/ dk ile 20 t dakika gitmiştir. Birisi gittiği yol, diğe ri dönüş yoludur. İki yol da birbirine eşit olduğuna göre, 30t 20(20 t) 30t 400 20t 50t 400 t 8 dakikadır. En uzak mesafe 30t 30.8 240 metredir. Örnek: 150 metre uzunluğundaki bir tren 250 m’lik bir tüneli 20 saniyede geçiyor. Buna göre, trenin hızı kaç km/sa tir? www.matematikkolay.net Çözüm: Tren, tünelden tamamen çıkana kadar hem tünel mesafesini gider hem de kendi boyu kadar mesafe gitmiş olur. Dolayısıyla tren 20 saniyede 400 metre mesafe git – 400 m miştir. Hızı 20 m / sn dir. 20 s Bunu km/ s aate çevirelim. 20 km 20 m 1000 20 1 sn 1 100 sa 3600 3600 36 720 km/ sa tir. 1 Örnek: Leyla, 08: 00 de evden çıkıp yürüyerek okula gittiğin – de 09: 00 da okula varmaktadır. Yine bir gün 08: 00 1 de yola çıkmış ama yolun ünü gittikten sonra 4 ödevini almayı unuttuğunu farketmiştir. Bu noktadan sonra koşarak eve dönüp, aynı hızla koşarak okuluna gitmiştir. Buna göre, Leyla’nın koşma hızının yürü – me hızına oranı kaçtır? Çözüm: Geri D Yolun tamamına 4x diyelim. 4x Yürüme Hızı dır. 60 dk 1 Yolun tamamını 60 dakikada yürüyorsa, ünü 4 15 dakikada yürür. 08: 50 de okula var ıyorsa 50 15 35 dakika koşmuştur. Koşarak gittiği mesafe x önme 4x 5x tir. 5x Koşma Hızı dır. O halde, 35 dk 5x Koşma hızı Yürüme hızı 35 4 x 5 60 35 7 60 15 4 15 dir. 7 Örnek: Yukarıdaki A mumu yakıldığında 10 dakikada, B mumu ise 18 dakikada bitmektedir. Buna göre, her ikisi aynı anda yakıldık tan kaç dakika sonra boyları eşit olur? Çözüm: 30 cm A mumunun erime hızı 3 cm / dk dır. 10 dk 18 cm B mumunun erime hızı 1 cm / dk dır. 18 dk t dk sonra A mumunun boyu 30 3t olur. B mumunun boyu 18 t olur. İkisi nerde eşit olur , bulalım. 30 3t 18 t 12 2t t 6 dakikada eşit olur.

