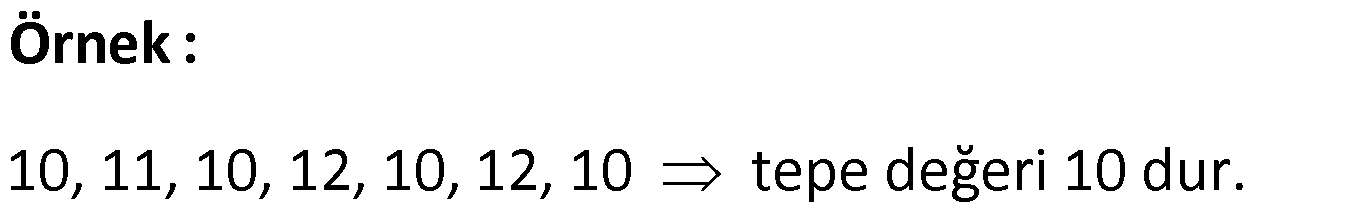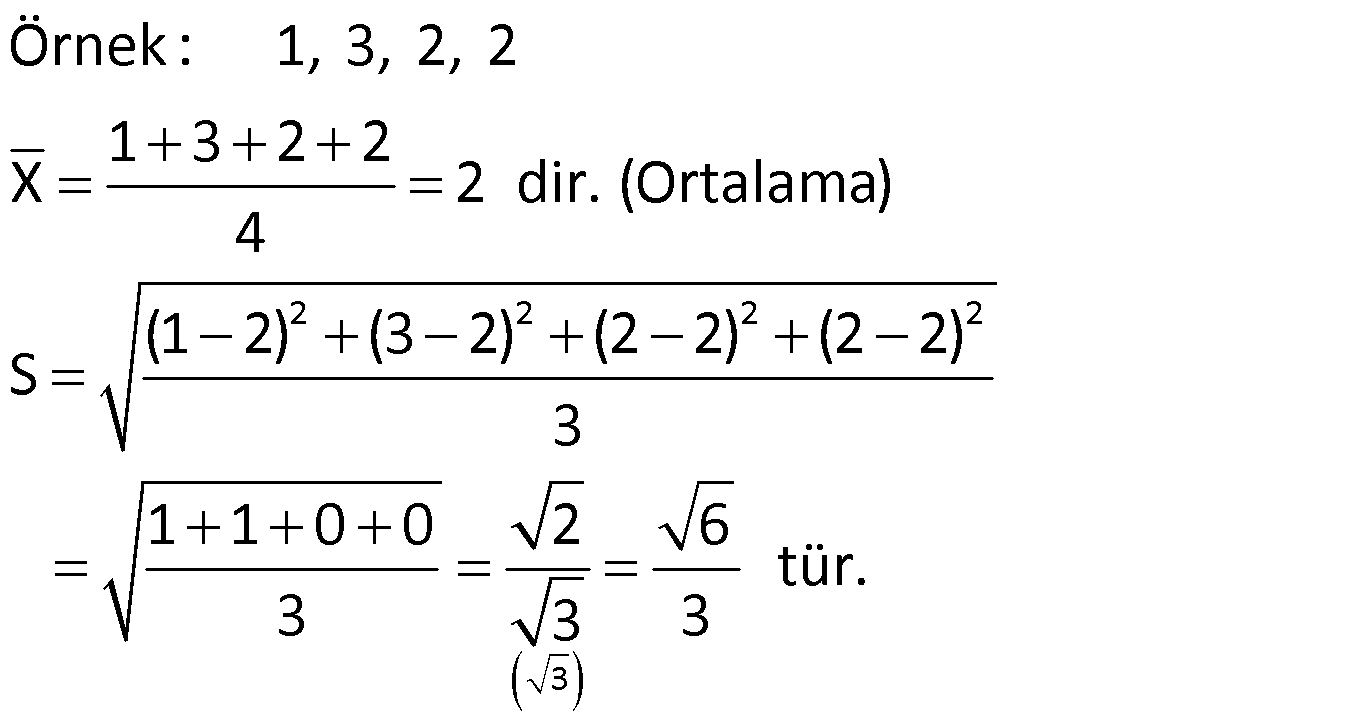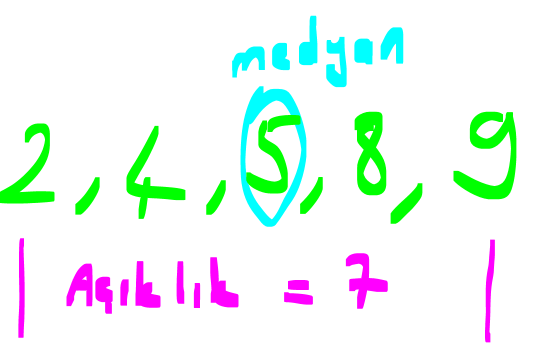 Sürekli Veri: Belirli bir aralıkta her değeri alabilen verilere sürekli veri denir.
Sürekli Veri: Belirli bir aralıkta her değeri alabilen verilere sürekli veri denir.
Örneğin, bir bebeğin ağırlığının 3,3 kg dan 6 kg’a geçiş aşaması.
Bu bebek, 3,3 kg ile 6 kg arasındaki tüm sayısal değerleri alabildiği için bu veri sürekli bir veridir.
Kesikli veri: Her sayısal değeri alamadığı için, bazı veriler sürekli gösterilemez.
Örneğin: Bir apartmanda oturan kişi sayısını doğal sayılarla ifade edebiliriz. 17/2 gibi bir kesirli sayıyla ifade edemeyiz. Bu sebeple kesikli veri oluşur.
MERKEZİ EĞİLİM ÖLÇÜLERİ

MERKEZİ YAYILIM ÖLÇÜLERİ


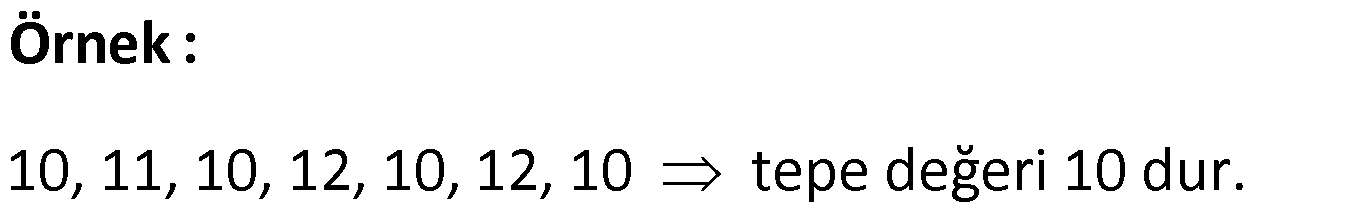



Standart Sapma
Standart sapma bize, veriler arasındaki değişkenlik hakkında bilgi verir.
Standart sapma ne kadar fazla ise, veriler o derece düzensiz, tutarsız, istikrarsızdır.

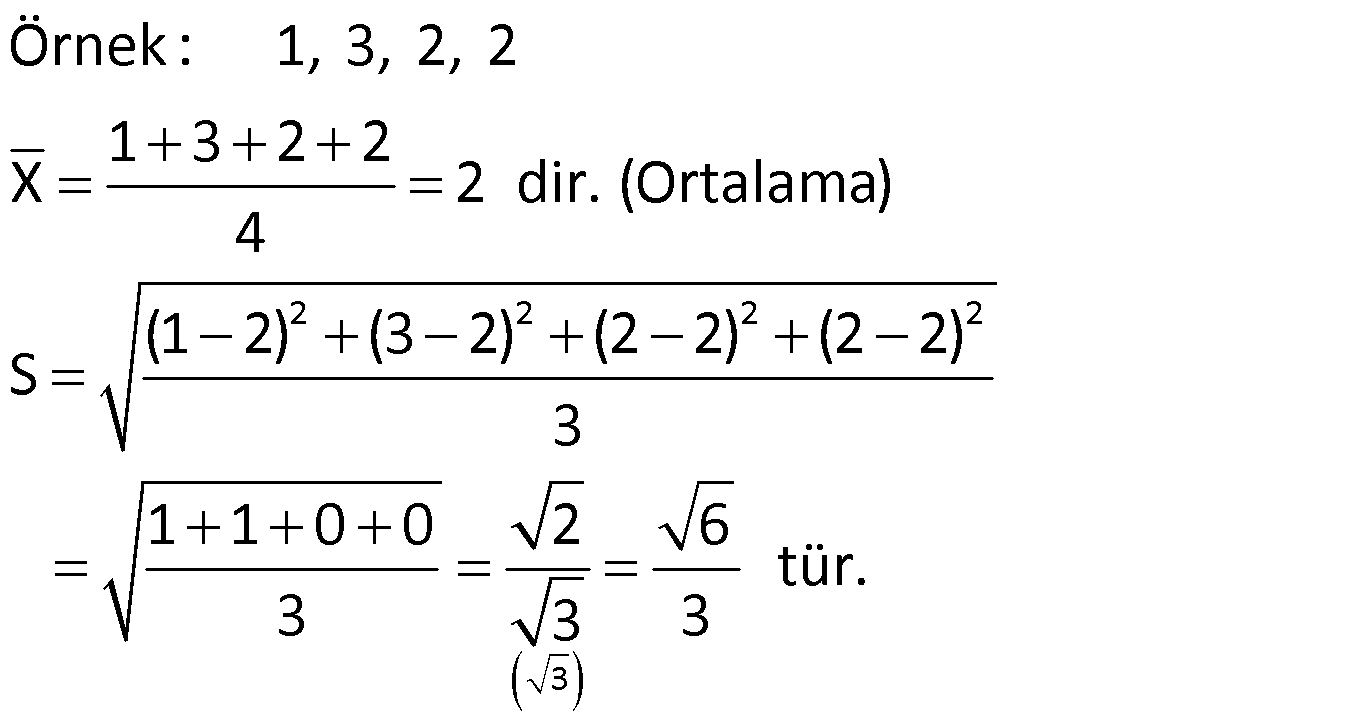
VERİLERİN GRAFİKLE GÖSTERİLMESİ
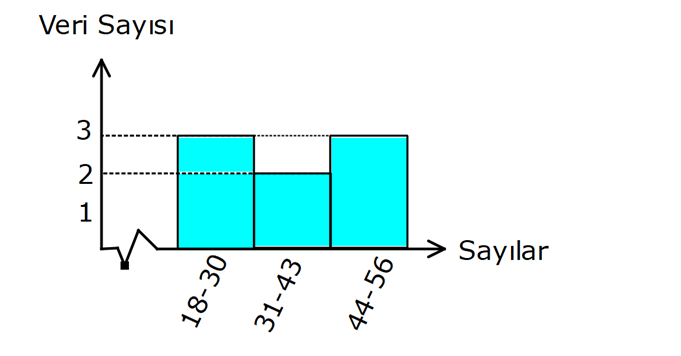
Histogram

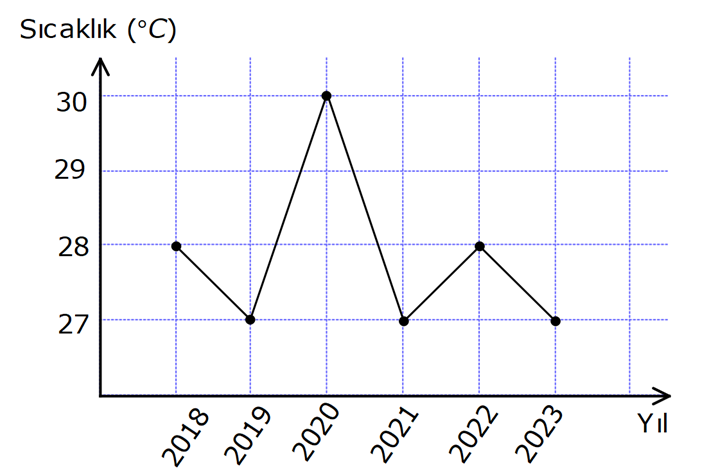
Çizgi Grafik

Örnek:
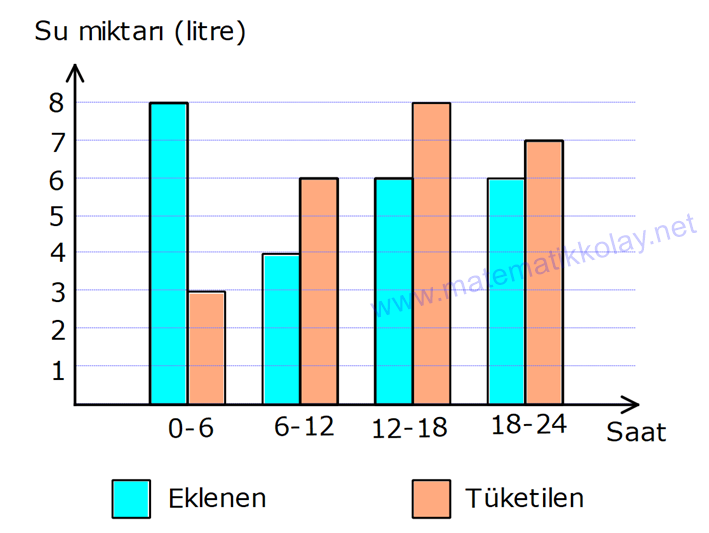
Sütun Grafiği
Veri gruplarının değişimini, gelişimini göstermek veya verileri kıyaslamak içim sütun grafiğinden yararlanılır.
Örnek:
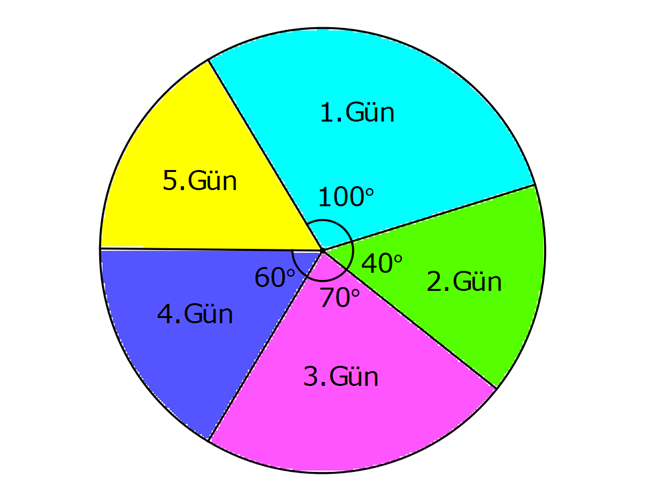
Daire Grafiği
Verilerin, bütüne oranını görmek için kullanılan bir grafiktir. Dairenin tamamı 360 derecedir.
Örnek:
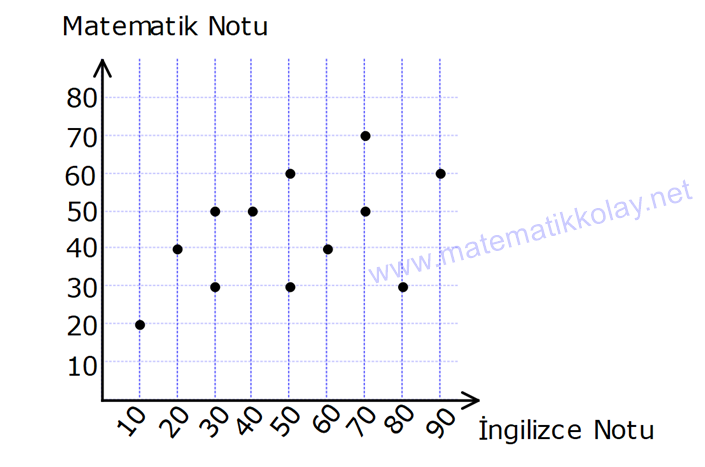
Serpme Grafiği (Fen Lisesi)
İki veriyi karşılaştırmak için, koordinat sisteminde nokta şeklinde gösterdiğimiz grafiklerdir. Bu grafiklerden değişimin yönünü tayin edebiliriz. Bunlar, pozitif yönlü, negatif yönlü veya düzensiz değişimler olabilir.
Örnek:
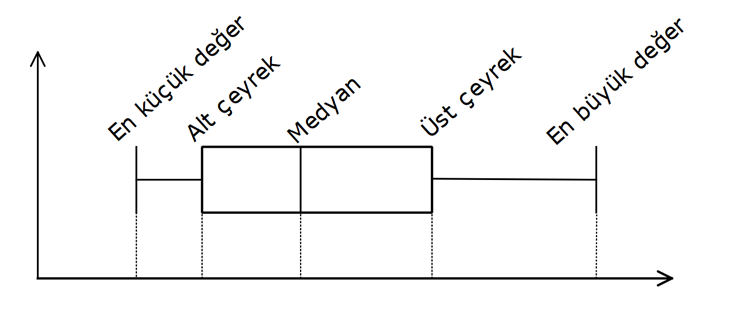
Kutu Grafiği (Fen Lisesi)
Bir veri grubunun merkezi yayılım ölçüleriyle ifade edildiği grafiklerdir.
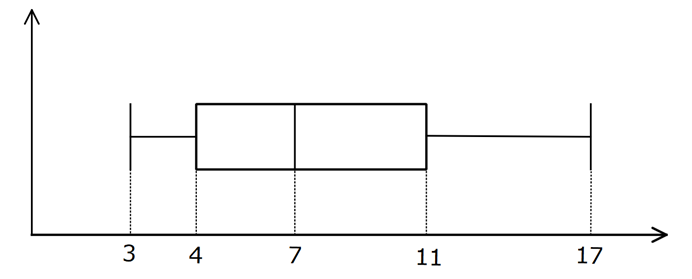
Örnek:

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
VERİ (MERKEZİ EĞİLİM VE YAYILIM ÖLÇÜLERİ) VE GRAFİKLER www.matematikkolay.net Sürekli Veri: Belirli bir aralıkta her değeri alabilen verilere sürekli veri denir. Örneğin, bir bebeğin ağırlığının 3,3 kg dan 6 kg’a geçiş aşaması. Bu bebek, 3,3 kg ile 6 kg arasındaki tüm sayısal değerleri alabildiği için bu veri sürekli bir veridir. Kesikli veri: Her sayısal değeri alamadığı için, bazı veriler sürekli gösterilemez. Örneğin: Bir apartmanda oturan kişi sayısını doğal sayılarla ifade edebiliriz. 17/2 gibi bir kesirli sayıyla ifade edemeyiz. Bu sebeple kesikli veri oluşur. MERKEZİ EĞİLİM ÖLÇÜLERİ 1 2 n Tüm verilerin toplamının veri sayısına bölümüne denir. Tüm veriler Ortalama Veri Sayısı x x … x X n aritmetik ortalama Tüm veriler küçükten büyüğe doğru sıralandığında tam ortadaki terime ) denir. Veri sayısı çift olduğunda, tam ortadaki terim olmayacaktır. Bu durumda, ortadaki 2 terimin ortalaması alını ortanca (medyan Medyan (Ortanca) 3 5 Medyan 4 2 r. 1, 2, 2, 4, 5 , 6, 8, 11, 18 Medyan 5 tir. 1, 2, 2, 3, 5 , 6, 8, 11 Medyan 4 tür. Örnekler : Bir veri grubunda en çok tekrar eden veriye ) denir. Tepe değeri, birden fazla olabilir. Bütün veriler eşit sayıda tekrar ediyorsa tepe değeri yoktur. tepe değeri (mod 10, 11, 10, 12, 10, 12, 10 tepe de ğeri 10 dur. Örnek : MERKEZİ YAYILIM ÖLÇÜLERİ , bir veri grubunun en büyüğü ile en küçüğü arasındaki farktır. Açıklık En En küçük büyük 5 , 8, 9, 10, 11, 11, 12, 14 Açıklık 14 5 9 dur. Örnek : 1 medyandan küçük değerlerdir. medyandan büyük değerlerdir. Alt grubun medyanıdır. Üst grubun medyanıdır. Üst 3 (FEN LİSESİ İÇİN) Alt grup : Üst grup : Alt çeyrek (Q ): Üst çeyrek (Q ): Çeyrekler açıklığı (Q): medyan Alt grup Üst grup Alt Çeyrek 5 Üst Çeyrek 11 çeyrek ile alt çeyrek arasındaki farktır. Örnek : 3, 5, 6 8 , 9, 11, 17 Çey rekler açıklığı 11 5 6 dır. Standart Sapma Standart sapma bize, veriler arasındaki değişkenlik hakkında bilgi verir. Standart sapma ne kadar fazla ise, veriler o derece düzensiz, tutarsız, istikrarsızdır. Standart sapmayı hesaplamak için, 1. Aritmetik ortalama bulunur. (X) 2. Her bir verinin aritmetik ortalaması ile farkı bulunup, kareleri toplanır. 3. Bu toplam, veri sayısının 1 eksiğine bölünür ve 2 2 2 1 2 n karekökü alınır. Çıkan sonuç, bize standart sapmayı verir. Formülü şu şekildedir: (x X) (x X) … (x X) S n 1 www.matematikkolay.net 2222 3 Örnek : 1, 3, 2, 2 1 3 2 2 X 2 dir. (Ortalama) 4 (1 2) (3 2) (2 2) (2 2) S 3 1 1 0 0 2 6 tür. 3 3 3 VERİLERİN GRAFİKLE GÖSTERİLMESİ Histogram Verilerin çok olduğu durumlarda, daha özet ve daha anlaşılır bir grafik için histogram tercih edilir. Histogram çizerken, bitişik dikdörtgen sütunlar kullanılır. Histogram için, ilk önce veri grubunun açıklığı bulunur. Belirlenen grup sayısına bölünür. Çıkan sonuçtan büyük, en küçük tam sayı grup genişliğini belirler. Daha sonra, en küçük sayıdan başlayarak grup aralıkları yazılır ve burada kaç veri olduğu belirtilir. En sonunda histogram çizilir. 18, 21, 22, 32, 33, 46, 48, 55 veri grubunu 3 gruba ayırarak histogramla gösterelim. Buna göre, Açıklık 55 18 37 dir. 37 Grup genişliği 3 Grup genişliği 13 o Örnek : lacaktır. Şimdi tablo yapalım. 18 30 arası 3 veri 31 43 arası 2 veri 44 56 arası 3 veri Buna göre, şu şekilde bir histogram çizebiliriz: Çizgi Grafik Noktasal verilerin, çizgilerle birleştirilmesi sonucu, çizgi grafikler oluşur. Çizgi grafikler daha çok, iki değişken arasındaki artma ya da azalma eğilimlerini incelemek için kullanılır. Örnek: Sütun Grafiği Veri gruplarının değişimini, gelişimini göstermek veya verileri kıyaslamak içim sütun grafiğinden yararlanılır. Örnek: www.matematikkolay.net Daire Grafiği Verilerin, bütüne oranını görmek için kullanılan bir grafiktir. Dairenin tamamı 360 derecedir. Örnek: Serpme Grafiği (Fen Lisesi) İki veriyi karşılaştırmak için, koordinat sisteminde nokta şeklinde gösterdiğimiz grafiklerdir. Bu grafiklerden değişimin yönünü tayin edebiliriz. Bunlar, pozitif yönlü, negatif yönlü veya düzensiz değişimler olabilir. Örnek: Kutu Grafiği (Fen Lisesi) Bir veri grubunun merkezi yayılım ölçüleriyle ifade edildiği grafiklerdir. Örnek: medyan Alt grup Üst grup Alt Çeyrek 4 Üst Çeyrek 11 3, 4, 6, 7 , 9, 11, 17 Buna göre, kutu grafiğini aşağıdaki gibi çizebiliriz.
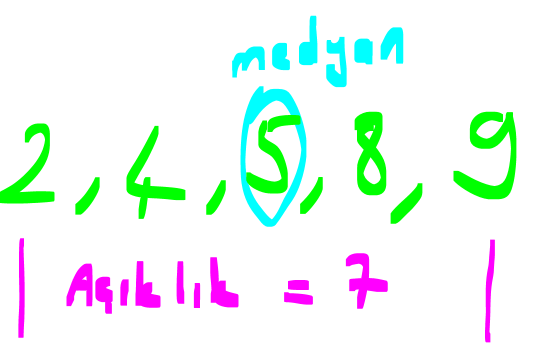 Sürekli Veri: Belirli bir aralıkta her değeri alabilen verilere sürekli veri denir.
Sürekli Veri: Belirli bir aralıkta her değeri alabilen verilere sürekli veri denir.