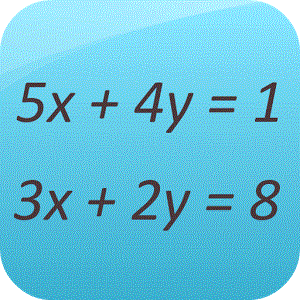
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
TANIM
![]() olmak üzere,
olmak üzere,
![]()
denklemine birinci dereceden bir bilinmeyenli denklem denir.
![]() sayısına denklemin kökü denir.
sayısına denklemin kökü denir.
Ç=![]() kümesine denklemin çözüm kümesi denir.
kümesine denklemin çözüm kümesi denir.
![]() olduğunda
olduğunda ![]() ise çözüm kümesi reel sayılardır.
ise çözüm kümesi reel sayılardır.
![]() olduğunda
olduğunda ![]() ise çözüm kümesi boş kümedir.
ise çözüm kümesi boş kümedir.
Örnek:
![]() denklemi x’e bağlı 1.dereceden bir bilinmeyenli denklem ise, denklemin çözüm kümesi nedir?
denklemi x’e bağlı 1.dereceden bir bilinmeyenli denklem ise, denklemin çözüm kümesi nedir?
Çözüm:
![]() nin katsayısı 0 olmalıdır. Bu sebeple
nin katsayısı 0 olmalıdır. Bu sebeple ![]() tür.
tür.
![]()
![]()
![]()
![]()
Ç![]() buluruz.
buluruz.
Örnek:
![]() denkleminin çözüm kümesi nedir?
denkleminin çözüm kümesi nedir?
Çözüm:
![]()
![]()
Ç![]() dir.
dir.
(Çözüm Kümesi Boş Kümedir.)
Örnek:
![]() denkleminin çözüm kümesi tüm Reel sayılar ise
denkleminin çözüm kümesi tüm Reel sayılar ise ![]() nedir?
nedir?
Çözüm:
![]()
![]()
![]()
![]()
![]()
EŞİTLİĞİN ÖZELİKLERİ
1. Her iki tarafa aynı sayıyı ekleyebilir, iki taraftan da aynı sayıyı çıkarılabiliriz.
Örnek:
![]()
![]()
2.Her iki tarafı aynı sayı ile çarpabilir, aynı sayıya bölebiliriz(Bölen sayı 0 olamaz.)
Örnek:
![]()
![]()
3.Her iki tarafın aynı kuvvetini alabiliriz.
Örnek:
![]()
![]()
4.Aynı sayıya eşit olan iki sayı, birbirine eşittir.
![]()
Örnek:
![]()
5.İki eşitlik taraf tarafa toplanabilir, çıkarılabilir, çarpılabilir ve bölünebilir.
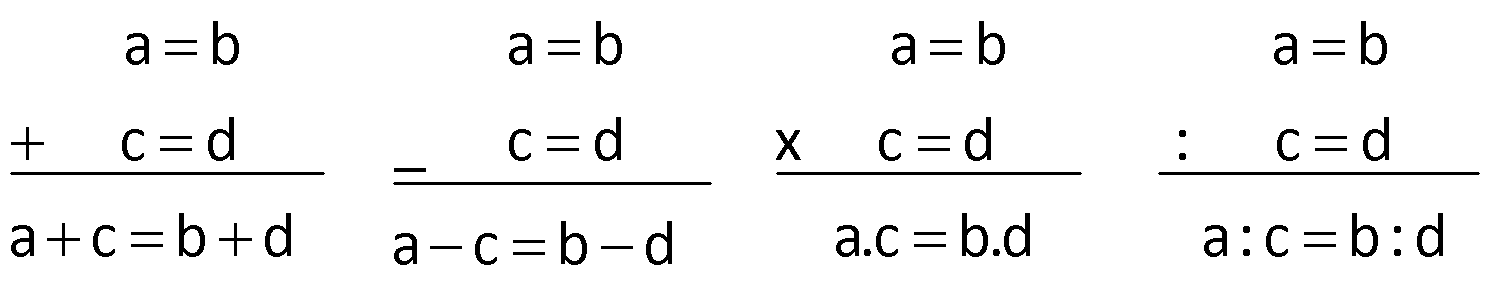
BİRİNCİ DERECEDEN İKİ BİLİNMEYENLİ DENKLEM SİSTEMİ
![]() sabit gerçek sayılar,
sabit gerçek sayılar, ![]() sıfırdan farklı olmak üzere,
sıfırdan farklı olmak üzere,
![]()
şeklinde yazılan ifadelere birinci dereceden iki bilinmeyenli denklem denir.
Bu denklemlerden birden fazla bulunursa, bu gruba birinci dereceden iki bilinmeyenli denklem sistemi denir.
Örnek:
![]()
Çözüm Kümesinin Bulunması
1. Yok Etme Yöntemi: Denklem sisteminde bilinmeyenlerden herhangi birinin katsayısı diğer denklemdeki aynı değişkenin
katsayısı ile mutlak değerce eşit ve işaretleri ters olacak şekilde düzenlendikten sonra denklemler taraf tarafa toplanarak değişkenlerden biri yok edilir.
Örnek:

Çözüm:
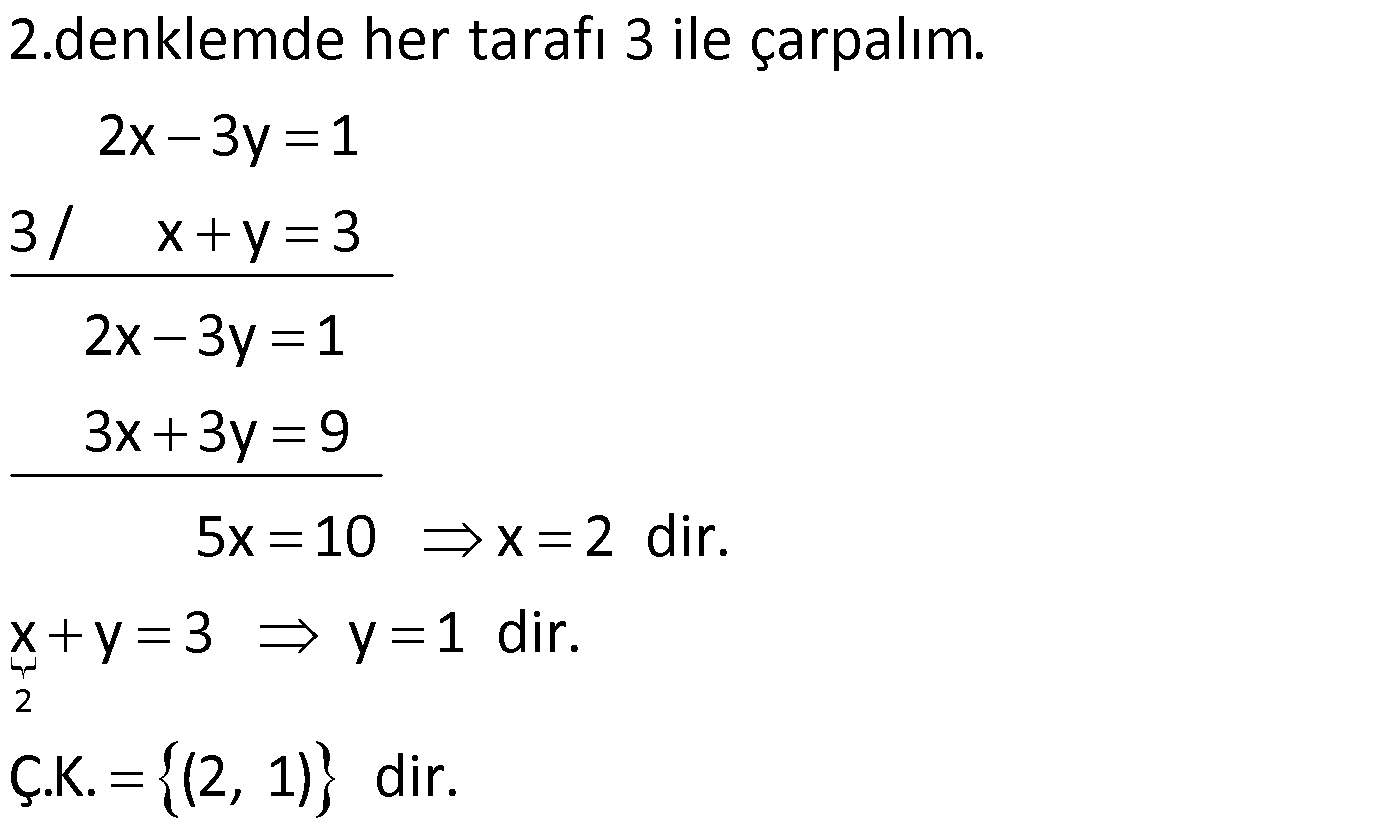
2.Yerine Koyma Yöntemi
Denklem sisteminde bulunan değişkenlerden biri diğeri cinsinden bulunur. Bulunan bu değer diğer denklemde yerine yazılır.
Örnek:

Çözüm:

3.Eşitleme Yöntemi: Her iki denklemde de aynı bilinmeyen yalnız bıraklılarak elde edilen ifadeler birbirine eşitlenir.
Örnek:

Çözüm:
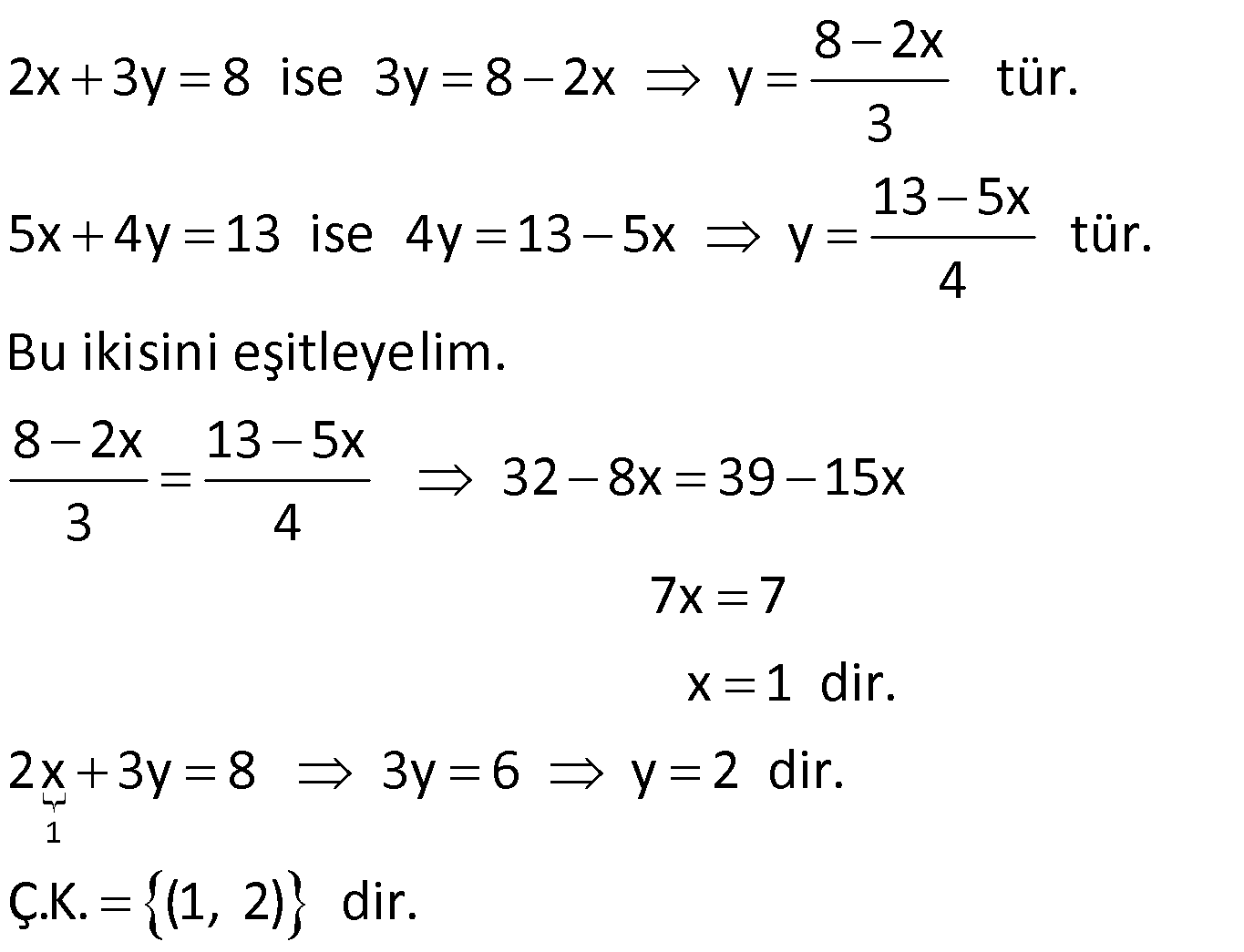
Grafik
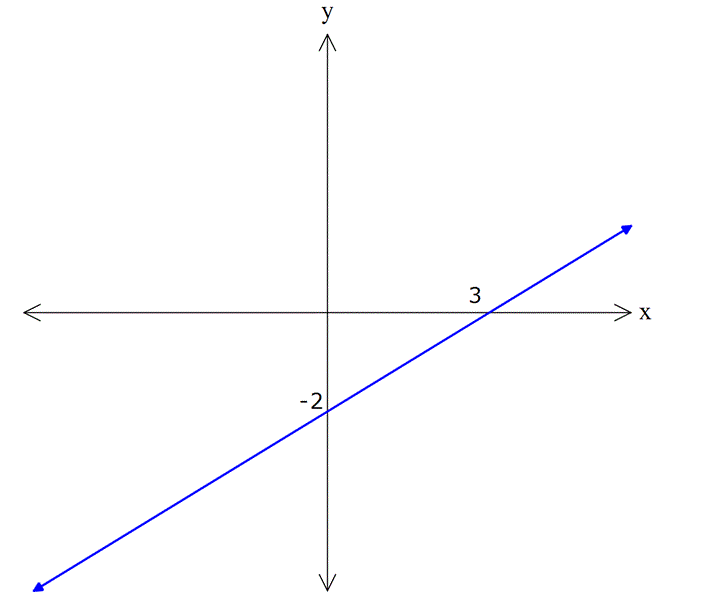
![]() şeklindeki birinci dereceden iki bilinmeyenli her denklem, koordinat düzleminde bir doğru belirtir.
şeklindeki birinci dereceden iki bilinmeyenli her denklem, koordinat düzleminde bir doğru belirtir.
Örnek:

Çözüm:

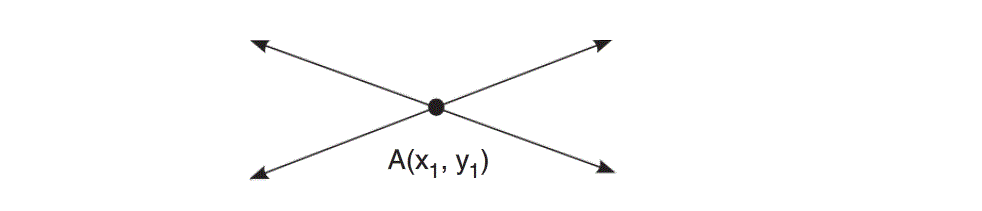
Denklem Sistemindeki Doğrular
1)

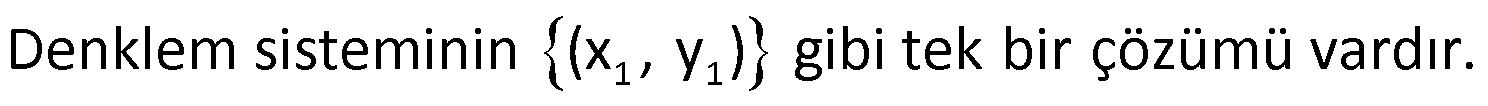
2)

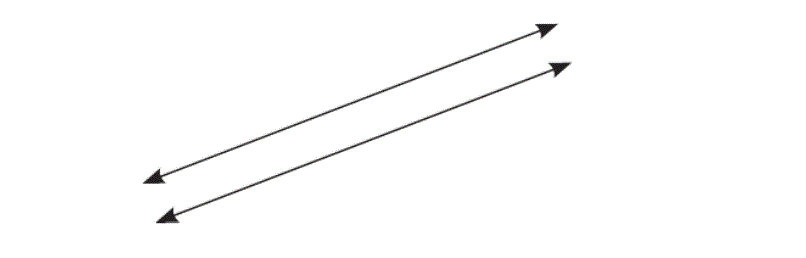
Denklem sisteminin çözüm kümesi boş kümedir.
3)
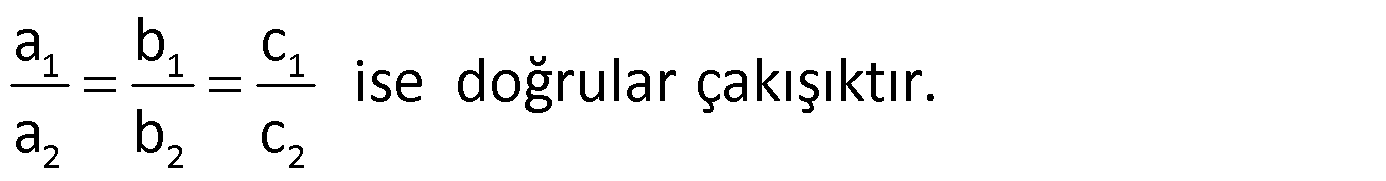

Çözüm kümesi sonsuzdur.
Örnek:
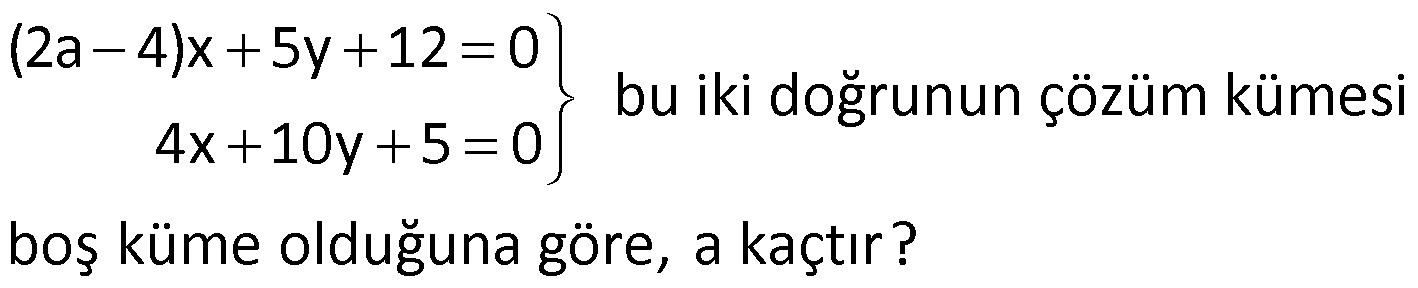
Çözüm:

Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
Çözümlü Sorular veya Çıkmış Sorular için Tıkla

