Bu bölümde Önermeler ile ilgili 10 adet soru bulunmaktadır. Sorularınızı çözdükten sonra düşündüğünüz şıkka tıklayarak doğru yapıp yapmadığınızı kontrol edebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. İyi Çalışmalar…
1.SORU
 |  |  |  |  |
Çözüm için Tıklayınız.
2.SORU
| | | | | |
Çözüm için Tıklayınız.
3.SORU
| | | | | |
Çözüm için Tıklayınız.
4.SORU
| | | | | |
Çözüm için Tıklayınız.
5.SORU
| | | | | |
Çözüm için Tıklayınız.
6.SORU
| | | | | |
Çözüm için Tıklayınız.
7.SORU
| | | | | |
Çözüm için Tıklayınız.
8.SORU
| | | | | |
Çözüm için Tıklayınız.
9.SORU
| | | | | |
Çözüm için Tıklayınız.
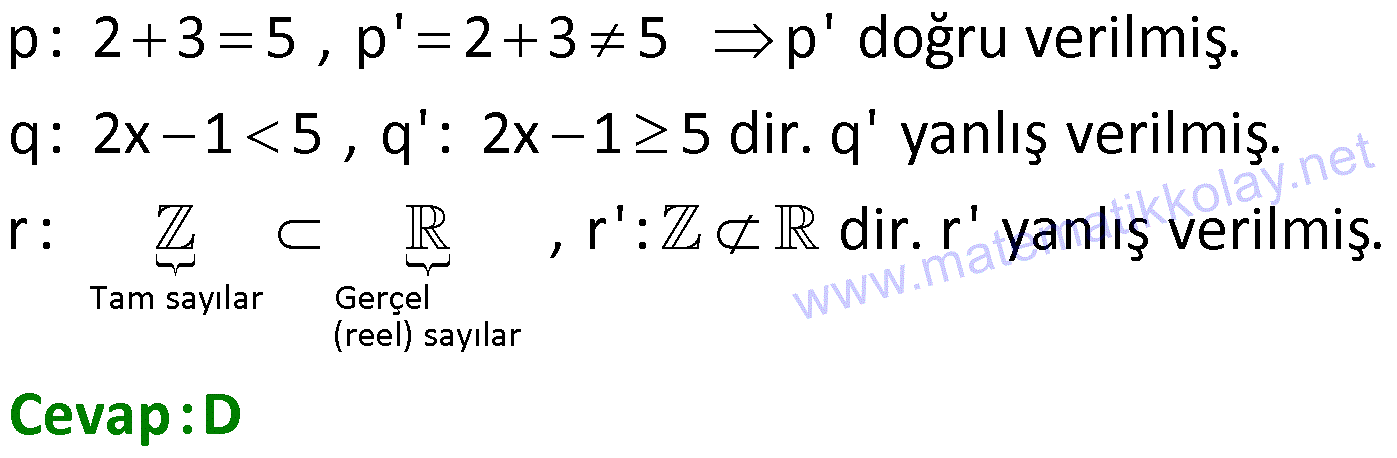
10.SORU
| | | | | |
Çözüm için Tıklayınız.
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
Bu içerik www.matematikkolay.net tarafından özel olarak hazırlanmıştır. Kısmen dahi olsa başka platformlarda izinsiz bir şekilde yayınlanamaz, basılamaz. (Sadece öğretmenlerimiz, ders ortamında kullanmak üzere kullanabilirler.)
Mantık (Önermeler) 1) o Aşağıdaki ifadelerden kaç tanesi önerme belirtir? I. Bugün hava güzel. II. Görüyorum ki derslerine hiç çalışmıyorsun. III.Suyun kaynama noktası 90 C dir. IV. Bugün okula birlikte gidelim mi? V. Türkiyede 81 il vardır. A) I ve II B) II ve V C) III ve V D) I, IV ve V E) III ve IV Çözüm: z Doğru veya yanlış kesin hüküm bildiren ifadeler önerme belirtir. Emir ve soru cümleleri önerme belirtm Bugün hava güzel ifadesi öznel bir ifadedir.Kes e in doğru ya da kesin yanl z ış şeklinde . yorumlanama o . Görüyorum ki derslerine hiç çalışmıyorsun ifadesi de öznel bir ifade olduğu için önerme belirtmez. Suyun kaynama noktası 90 C dir ifade I si, doğruluğu ya . öncül önerme değildir. II. öncül önerme değildir. da yanlışlığı kanıtlanabilir bir ifade olduğundan önermedir. Bugün okula gidelim mi? ifadesi bir soru cümlesi olduğundan önerme değildir. Türkiye’de 81 il IV. öncül önerme değ .III. öncül l öne . rm i ir edir d vardır ifadesi, doğruluğu ya da yanlışlığı kanıtlanabilir bir ifade olduğundan önermedir. V. öncül önermedir. Cevap : C 2) o Aşağıdakilerden hangisi yanlış bir önermedir? A) İki basamaklı rakamları farklı en büyük tek sayı 97 dir. B) Üçgenin iç açıları toplamı 180 dir. C) 0 sayısı ne pozitiftir ne de negatiftir. D) En küçük sayma sayısı 1 dir. E) Tüm asal sayılar tektir. o İki basamaklı rakamları farklı en büyük tek sayı 97 dir. Üçgenin iç açıları toplamı 180 dir. 0 sayısı nötrdür. En küçük say A) şıkkı doğru bir önermedir. B) şıkkı doğru önermedir. C şıkkı doğru önermedir. ma sayısı 1 dir. Bir tane çift asal sayı vardır (2). D şıkkı doğru ö E şıkkı yanlı E . ş önerm n edir ermedir . Cevap : 3) Aşağıdaki önermelerden hangisinin doğruluk değeri 1 dir? A) 0′ dan farklı çift bir doğal sayının tüm doğal sayı kuvvetleri çifttir. B) Herhangi iki asal sayının toplamı daima çifttir. C) Tek sayıların 2 3 tüm tam sayı kuvvetleri de bir tek sayıdır. D) Ardışık iki tam sayının çarpımı daima çift bir tam sayıdır. E) x y ifadesi pozitif bir tam sayı ise y pozitif bir tam sayıdır. Çözüm: Mantık (Önermeler) 0′ dan farklı çift bir doğal Bir önerme doğruysa doğruluk sayının tüm doğal sayı kuvvetl değeri 1 dir. Bir önerme yanlı eri çift değildir. Çünkü 0 da ş ise doğruluk değeri n farklı tüm sayıların 0 dır. 0. kuvveti 1 e eşittir. 1 tek bir sayıdır. Asal sayılar 2 dışında hep tek sayılardır.Tek iki asal sayının toplamı çifttir. Fakat 2 ile başka bir asal sayının toplamı tektir. A) şıkkının doğruluk değeri 0 dır. Tek sayıların tüm doğal sayı kuvvetleri tektir. Fakat negatif tam sayı kuvvetleri rasyonel sayıdır. Paydası 1 den farklı olan rasyonel sayılarda teklik çiftlik aranamaz. B) şıkkının doğruluk değeri 0 dır. 2 3 3 Ardışık iki tam sayıdan biri tek ise diğeri çifttir. Bu yüzden çarpımları çifttir. x y 0 y pozitifse y de pozitiftir.Fakat y kökl D) şıkkının doğruluk C) şıkkının doğruluk değeri 1 değeri 0 dır. dir. 2 ü bir ifade olabilir. Küpü alınınca veya x ile çarpılınca tam sayı olmuş olabilir. E) şıkkının doğruluk değeri 0 dır Doğru C . evap : D 4) Aşağıdaki önermelerin denklikleri hangi şıkta doğru verilmiştir? p: Şubat ayı 28 gündür. q: Dünyanın uydusu Ay dır. r: Güneş bir gezegendir. s: Dünyanın kendi ekseni etrafında dönmesi ile gece ve gündüz oluşur. A) p s B) p q C) q r D) p r E) r s Çözüm: Şubat ayı 4 yılda bir 29, diğer yıllar 28 gündür. Dünyanın uydusu aydır. q 1 Gü Doğruluk değeri aynı olan ö neş bir ışık kaynağı olduğu nermelere ndan geze p g denk ön en değil er yı meler de ldızdır nir . 0 . 0 r Dü nyanın kendi ekseni etrafında dönmesi ile gece ve gündüz oluşur. p r ve q s s 1 Cevap : D 5) 4 p : 3 81 dir. q: 2 4 : 2 1 3 tür. x y x y r: y dir. 2 2 Verilen önermelere göre aşağıdakilerden hangisi doğrudur? A) p 1 B) p q C) q 0 D) q r E) r 0 Çözüm: 4 4 2 3 81 dir. ( 3) 81 olsa doğru olurdu. p 0 2 4 : 2 1 2 2 1 3 tür.(işlem önceliği) q 1 x y x y x y (x y) x 2 2 2 y x y 2y y dir. 2 2 r 1 Buna göre q r olur. Cevap : D 6) 3n 1 farklı önermenin doğruluk tablosu 256 farklı durumdan oluştuğuna göre n farklı önermenin doğruluk tablosu kaç durumdan oluşur? A) 4 B) 8 C) 16 D) 32 E) 64 Çözüm: Mantık (Önermeler) n Önermelerinin doğruluk değerlerinin gösterildiği tabloya doğruluk tablosu denir. Bir önerme için tabloda 2 farklı durum vardır, 2 satır oluşur. 2 önerme için 4 satır oluşur. n tane önerme için 2 farklı d n 3n 1 3n 1 8 3 urum vardır, 2 e satır oluşur. 2 256 2 2 3n 1 8 3n 9 n 3tür. 3 tane ön rmenin doğruluk tablosu 2 8 farklı durumdan oluşur. Cevap : B 7) 7 önermeden 3 ü özdeş ise doğruluk tablosu kaç farklı durumdan oluşur? A) 128 B) 64 C) 32 D) 16 E) 8 Çözüm: 5 7 önermenin 3 ü birbiriyle aynı ise tabloda farklı durum oluşturmazlar. 3 ü tek bir önerme gibi düşünülür. 4 1 5 önerme var gibi değerlendirilir. 2 32 farklı durum oluşur. Cevap : C 8) “Tam sayılar birer rasyonel sayıdır.” önermesinin değili(olumsuzu) aşağıdakilerden hangisidir? A) Rasyonel sayılar birer tam sayıdır. B) Rasyonel sayılar birer tam sayı değildir. C) Tam sayılar birer rasyonel sayı değildir. D) Tam sayılar birer doğal sayıdır. E) İrrasyonel sayıllar birer tam sayı değildir. Çözüm: ” B . ” r T ö a e m m n s n a h y k ı ü l ü ar e i b t i r r l e e r i i r e a e s d yo d n l e n l y n sa n y r ı e d e ı ö r e ” m n ö n n d e ğ r l me o s u i s n z i ) n e i d i e n ğ e il m i n ğ ” i T m am e s i ay i ı e l y a n r e b i i ( r m e u r n r i a n s ş y s o l n e e ö l i s i a u y r ı ü i d e e m ğ e i d l d d r l r l ir. e olur. Cevap : C 9) Aşağıdaki önermelerden hangilerinin değilleri yanlış verilmiştir? p : 2 3 5 , p’: 2 3 5 q: 2x 1 5 , q’: 2x 1 5 r : , r’: A) Yalnız p B) Yalnız q C) p ve r D) q v e r E) p, q ve r Çözüm: Tam sayılar Gerçel (reel) sayılar p: 2 3 5 , p’ 2 3 5 p’ doğru verilmiş. q: 2x 1 5 , q’: 2x 1 5 dir. q’ yanlış verilmiş. r : , r’: dir. r’ yanlış verilmiş. Cevap : D 10) p q , q r ve p s olduğuna göre aşağıdakilerden hangisi yanlıştır? A) p 1 ise s 0 B) r s C) p 1 ise r 1 D) q’ s E) p’ r Çözüm: Verilenlere göre şıkları imceleyelim. A) p 1 olsun. p s p 1 ise s 0 doğru ud r. ) q B r, p s ve p q olduğundan r s doğrudur q . C) r ise p p q olduğundan r olur. p 1 ise r 0 olur. D r p 1 is r ) s ve e 1 ya l q n ış. r ise q s dir. q’ s doğr r. udu E) p q ve q r ise p r dir. p’ r do du ğru r. Cevap : C
