Soru Sor sayfası kullanılarak Türevin Anlamı konusu altında Dış Bükey, İç Bükey, Konveks, Konkav ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


Burdan sonraki sorular, Fen Lisesi Müfredatı için geçerlidir.
4.SORU
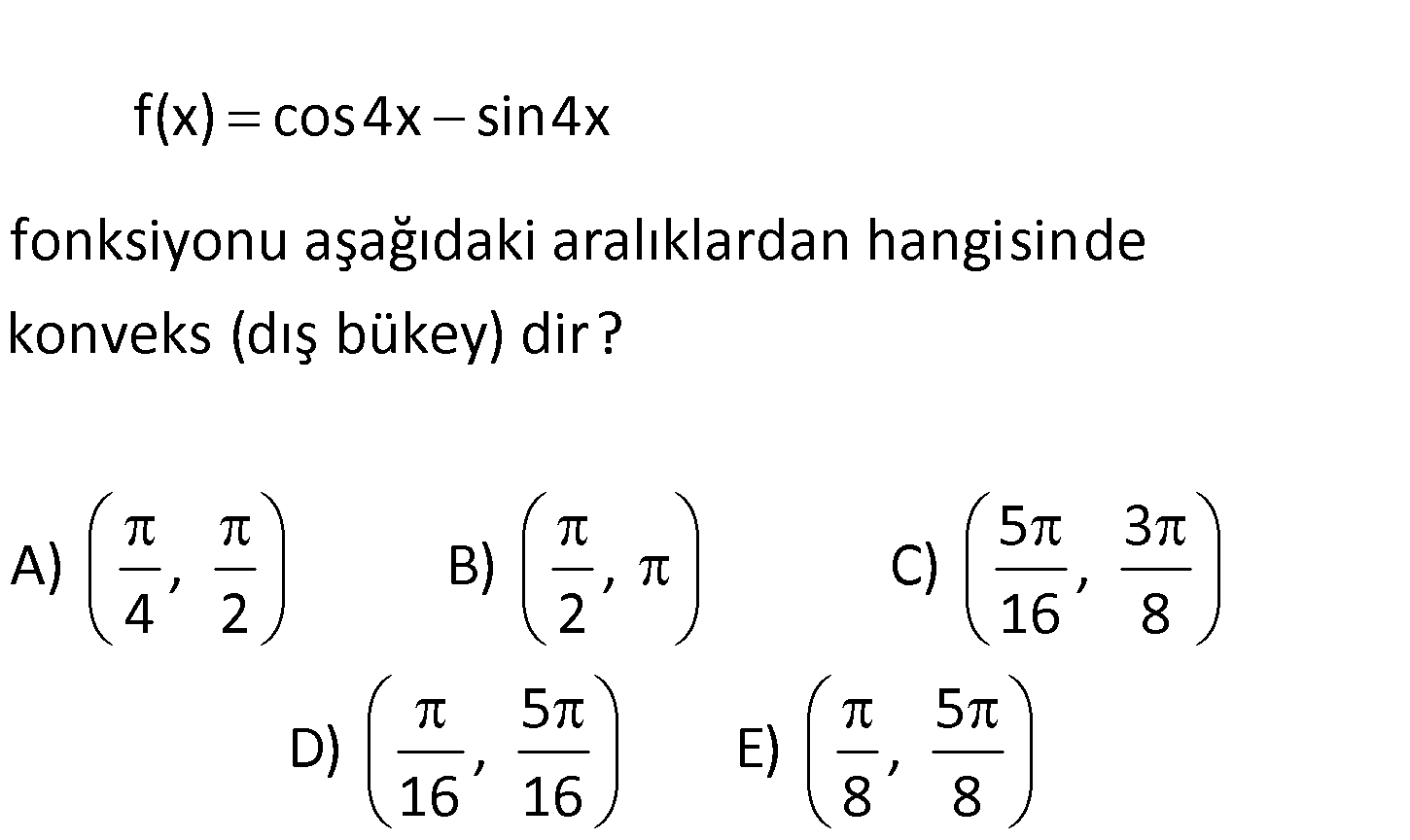

5.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 3 f(x) x 3x 1 fonksiyonunun iç bükey, dış bükey olduğu aralıkları ve dönüm noktasını bulunuz. 2 f ‘(x) 3x 3 f ”(x) 6x tir. 0’a eşitleyelim. f ”(x) 0 6x 0 x 0 dır. : Çözüm Dönüm noktası x 0 için f(x) 1 dir. Dönüm noktasının koordinatları 0,1 noktasıdır. x 0 için f ”(x) 0 olduğu için dış bükeydir. ,0 x 0 için f ”(x) 0 olduğu için iç bükeydir. 0, 131
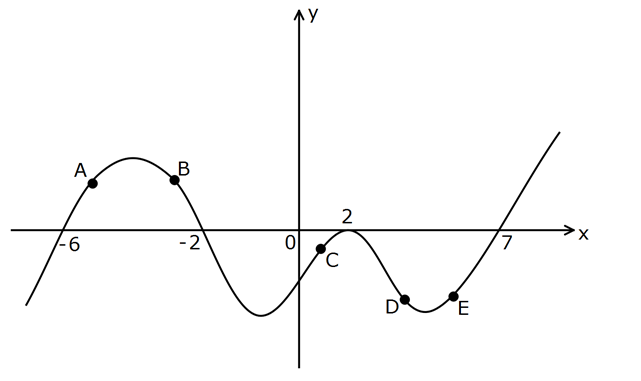
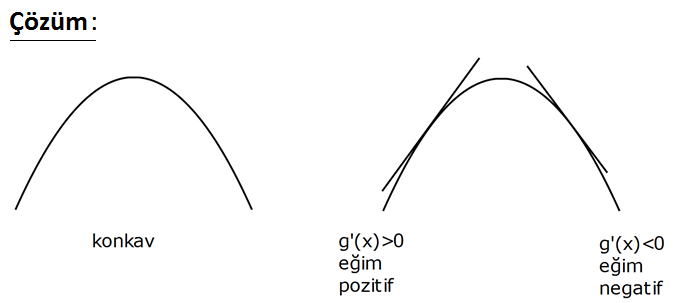
www.matematikkolay.net Şekilde y g(x) fonksiyonunun grafiği verilmiştir. g(x) üzerindeki hangi harfli noktada g'(x) 0 ve k onkav (eğrilik yönü aşağı) dır? A) A B) B C) C D) D E) E : Çözüm Şekilde gösterildiği gibi, aradığımız nokta aşağı yön – lü bir bükeyin içinde olmalı ve teğetinin eğimi negatif olmalı. Bu şartlara B noktası uyuyor. Cevap: B www.matematikkolay.net 174
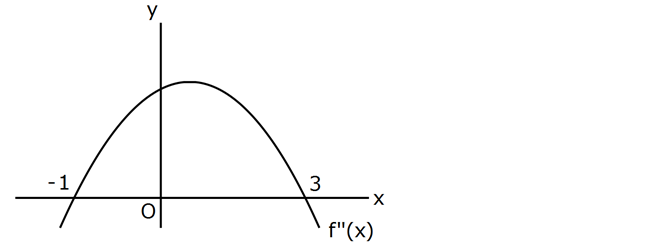
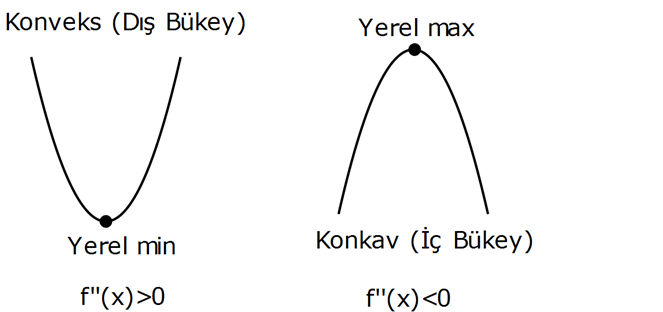
Şekilde f(x) in II. türevi olan f ”(x) fonksiyonunun grafiği verilmiştir. Buna göre, f(x) fonksiyon 1 1 u için aşağıdakilerden hangisi yanlıştır? A) f(x) in yerel maksimumu x ise 1 x 3 tür. B) x 1 ve x 3 de dönüm (büküm) noktası vardır. C) x 1 ve x 3 aralığında f ‘(x) 0 dır. D) f(x) in yerel 1 1 minimumu x ise 1 x 3 tür. E) 1 x 3 aralığında f ”(x) 0 dır. www.matematikkolay.net Bize fonksiyonun ikinci türevi verilmiş. x 1 ve x 3′ te dönüm noktası olduğunu görüyo – ruz. x : Çözüm 1 ve x 3 için 2.türevin negatif olduğunu, 1 x 3 için ise 2.türevin pozitif olduğunu görüyoruz. Bu bilgilere göre B, C ve E şıkları doğrudur. 2.türevin pozitif olması Konveks (Dış Bükey) demektir. Ko nveks’ te yerel minimum noktası olabilir. Bu sebeple D şıkkı doğru, A şıkkı yanlıştır. 175
www.matematikkolay.net f(x) cos4x sin4x fonksiyonu aşağıdaki aralıklardan hangisinde konveks (dış bükey) dir? A 4 ) 5 3 , B) , C) , 2 2 16 8 5 5 D) , E) , 16 16 8 8 f(x) cos4x sin4x fonksyonunun ikinci türevinin 0’dan büyük olduğu aralığı bulalım. f ‘( : x) 4si Çözüm n4x 4cos4x 4(sin4x cos4x) f ”(x) 16(cos4x sin4x) f ”(x) 0 konvekstir. 16(cos4x sin4x) 0 cos4x sin4x 0 cos4x sin4x Aynı açının kosinüsü, sinüsten küçükse bu a çı 5 ile arasında olmalıdır. 4 4 (Birim çemberden de bakabilir siniz.) 5 5 4x , x , buluruz. 4 4 16 16 20
www.matematikkolay.net x x fonksiyonunun konveks (dışbükey) olduğu aralık aşağıdakilerden 2e 4e hangi si y dir? 2 A) 5 , 5 4 2 2 B) , C) , 5 5 5 D) , E) 0, x x x x x x x İkinci türevi 0’dan büyükse konvekstir. 2e 4e y’ 5 2e 4e y” tir. 5 2e 4e 0 ? 5 2e 4 : Çözüm x x x x x x x x 2 e 0 e 2e 0 e 2e 2 e e e 2 her zaman geçerlidir. Buna göre; ( , ) aralığında konvekstir. 61


ilk soru yanlış çözülmüş
ikinci türev negatiftse konkav yani iç bükey
Uyarınız için teşekkürler. Ters yazılmıştı. Şimdi düzeltildi.