Soru Sor sayfası kullanılarak Temel Kavramlar konusu altında Farklı Temel Kavram Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

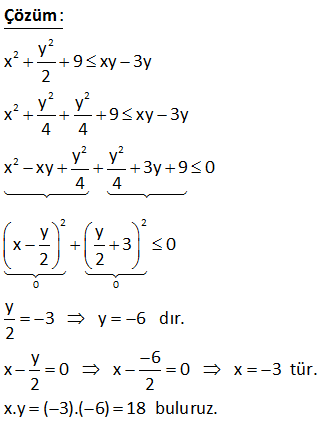
3.SORU


4.SORU


5.SORU
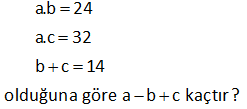

6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
3 AAA üç basamaklı ve A69260A7 sekiz basamaklı sayıdır. AAA A69260A7 olduğuna göre, A kaçtır? A) 2 B) 3 C) 4 D) 6 E) 9 www.matematikkolay.net 3 3 (AAA) …….7 ise Birler basamağındaki A sayısının küpü alındığında son basamağı 7 olan bir sayı elde edilmiş. Bu sadece A 3 iken sağlanır. (3 7) : 2 Çözüm 4 2 2 x ve y gerçek sayılardır. y x 9 x.y 3y 9 olduğuna göre, x.y çarpımı kaçtır? A) 24 B) 18 C) 16 D) 15 E) 12 www.matematikkolay.net 2 2 2 2 2 2 2 2 2 2 0 0 y x 9 xy 3y 2 y y x 9 xy 3y 4 4 y y x xy 3y 9 0 4 4 y y x 3 0 2 2 y 3 y 6 dır. 2 y 6 x 0 x 0 x 3 tür. 2 2 x.y ( 3).( 6) 18 buluruz. : Çözüm 37 2 x ve y sıfırdan farklı birer tamsayı olmak üzere, 5 15 x y 7 2 olduğuna göre, x y toplamının alabileceği en küçük değer kaçtır? A) 42 B) 40 C) 0 D) 42 D) 44 www.matematikkolay.net 5 Çözüm: 15 x 7 3 2 2 2 2 2 y 2 x 3y içler dışlar çarpımı yapalım. 7 2 2x 21y 21y x dir. 2 x’in bir tam sayı olabilmesi için, y bir çift sayı olmalıdır. y değeri sürekli pozitif olduğundan; y’yi mutlak değerce en küçük seç 2 meye çalışmalıyız. y 2 olsun. 21 2 21. 4 x 2 2 2 42 dir. Toplarsak; x y 42 2 40 buluruz. 193 2 a ve b tam sayılar olmak üzere, a b= a 4 , ? A) 2 B) 6 C) 9 D) 12 E) 15 olduğuna göre b nin en büyük değeri kaçtır www.matematikkolay.net 2 2 2 a a 16 16 b a 4 a 4 a 16 16 (a 4) (a 4) b b a 4 a : 4 Çözüm a 4 16 a 4 16 b a 4 a 4 a 4, 16 yı bölmek zorunda olduğundan buna uygun sayılar seçmeliyiz. a 3 veya a 12 olduğunda b 9 oluyor. Bunun dışında daha büyü bir b değeri bulunmuyor. 56 a.b 24 a.c 32 b c 14 olduğuna göre a b c kaçtır? www.matematikkolay.net 14 : a.b a.c 24 32 a.(b c) 56 a.14 56 a 4 tür. a.b 24 b 6 dır. a.c 32 c 8 dir. Buna göre; a b c 4 6 8 6 buluruz. Çözüm 62 www.matematikkolay.net a ve b pozitif tam sayı olmak üzere ab b 12 ise en büyük a b değeri kaçtır? : ab b 12 b(a 1) 12 b ve a 1’i birbirinden uzak seçmeliyiz. a 1 12 a 11 b 1 olur. a b 11 1 12 bulunur. Çözüm 99 2 a bir tam sayıdır. a 1 .a b olduğuna göre, aşağıdakilerden hangisi daima doğrudur? A) b, 4’ün katıdır. B) b doğal sayıdır. C) b tek sayıdır. D) b, 5’in katıdır. E) b, 3’ün katıdır. www.matematikkolay.net 2 a 1 a b a 1 a 1 .a b a 1 .a a 1 b b sayısı ardışık 3 sayının çarpımı olduğundan çarpanlardan biri muhakkak 3’ün katı olur. Buna göre b kesinlikle 3’ün katı olur : . Çözüm 132 x,y,z pozitif tam sayılardır. 48 x 1 1 1 25 y z 2 x y z ? : 48 x 1 1 1 1 z 2 olursa kesri ile 25 y z 2 2 beraber bir tam sayı oluşturur. 48 x 1 1 1 48 x 1 1 25 y 2 2 25 y 48 x 1 23 x 1 1 25 y 25 y x 22 ve y 25 tir. Buna göre; x y z 22 25 2 49 bu Çözüm luruz. 70 2 3 a ve b pozitif tam sayılardır. 3a 5b olduğuna göre, a nın alabileceği en küçük değerin rakamları toplamı kaçtır? A) 12 B) 18 C) 20 D) 25 E) 28 www.matematikkolay.net 2 3 3 3 3 3 3 4 2 2 2 3a 5b 5b a 3 a’nın tam sayı olabilmesi için b ‘ün içerisinde hem 3’ün hem 5’in k : atı olmalı. b 15 olur en az. 5.15 5.5 .3 a 5 .3 3 3 a 25 .3 25.3 75 dir. 7 5 12 bulunur. Çözüm 87 www.matematikkolay.net a, b ve c pozitif tam sayılar ve c b a dır. b a 40 c olduğuna göre, a b c toplamı ? A) 48 B) 64 C) 72 D) 84 E) 92 en büyük kaç olabilir b a 40 c b ‘yi ne kadar küçük alırsak,a, o kadar büyük c olur. b en az 2 olabilir.Çünkü b, c den büyük. c a 2 40 a 38 olur. Şimdi b, yi a’dan küçük en büyük çift sayı olarak seçelim. b 36 olur : . b 36 2 c Çözüm 36 2 c 18 dir. c 2 a b c 38 36 18 92 bulunur. 119 www.matematikkolay.net Toplama, çıkarma, çarpma ve bölme işlem – lerinden bir tanesi iki kez veya iki tanesi birer kez kullanılarak, üç tane 7 den aşağıdaki sayı – lardan h A) 0 B) angisi 1 C) 2 elde edilem D) 6 E) 7 ez? A) (7 7) x 7 0 B) Elde edilemez. C) (7 7) / 7 14 / 7 2 D) 7 (7 / 7) 7 1 6 E) 7 7 7 7 : Çözüm 146 www.matematikkolay.net m, n, p birer rakamdır. m n p 6 ? A) 7 B) 8 C) 9 D) 10 E) 12 koşulunu sağlayan kaç tane üç basamaklı mnp sayısı yazılabilir 6’dan küçük birbirinden farklı 3 sayı seçeceğiz ve bunlarla tek bir şekilde m n p şartlara uygun bir mnp sayısı yazabiliriz. O zaman , seçim sayısını bulmalıyız. 1,2,3,4 ve 5 rakamlarından 3 rakam s : Çözüm eçilecek. Seçim sayısı şu kombinasyondur : 5 5.4.3 60 10 buluruz. 3 3.2.1 6 47


8. soru da en küçük değeri sorsa çözümünüz doğru olurdu
Haklısınız. En küçük diye sınırlandırmak gerekiyordu. Şimdi düzeltildi. Uyarınız için teşekkürler.
Soru 2 de çözüm kısmında niçin y*2 /4 iki defa yazıldı açıklarmısınız ?
Tam kare ifadeleri gösterebilmek için.
y^2/2 ifadesini iki tane y^2/4 olarak yazabiliyoruz.
Diğer bileşenlerle birlikte tam kare ifadeler oluşuyor.
Ordan da sonuca varıyoruz.