Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomun Sıfırları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

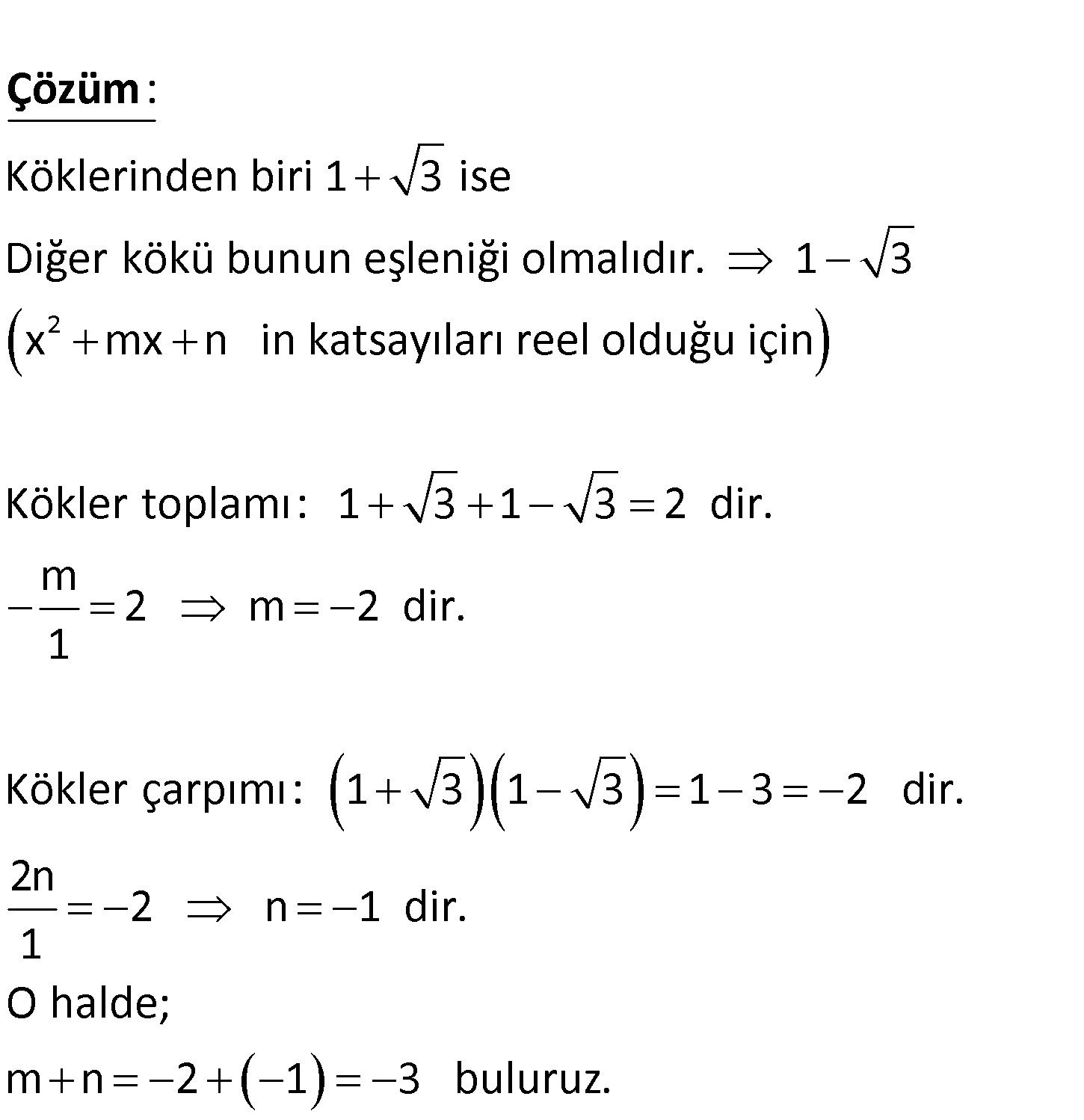
2.SORU


3.SORU


4.SORU

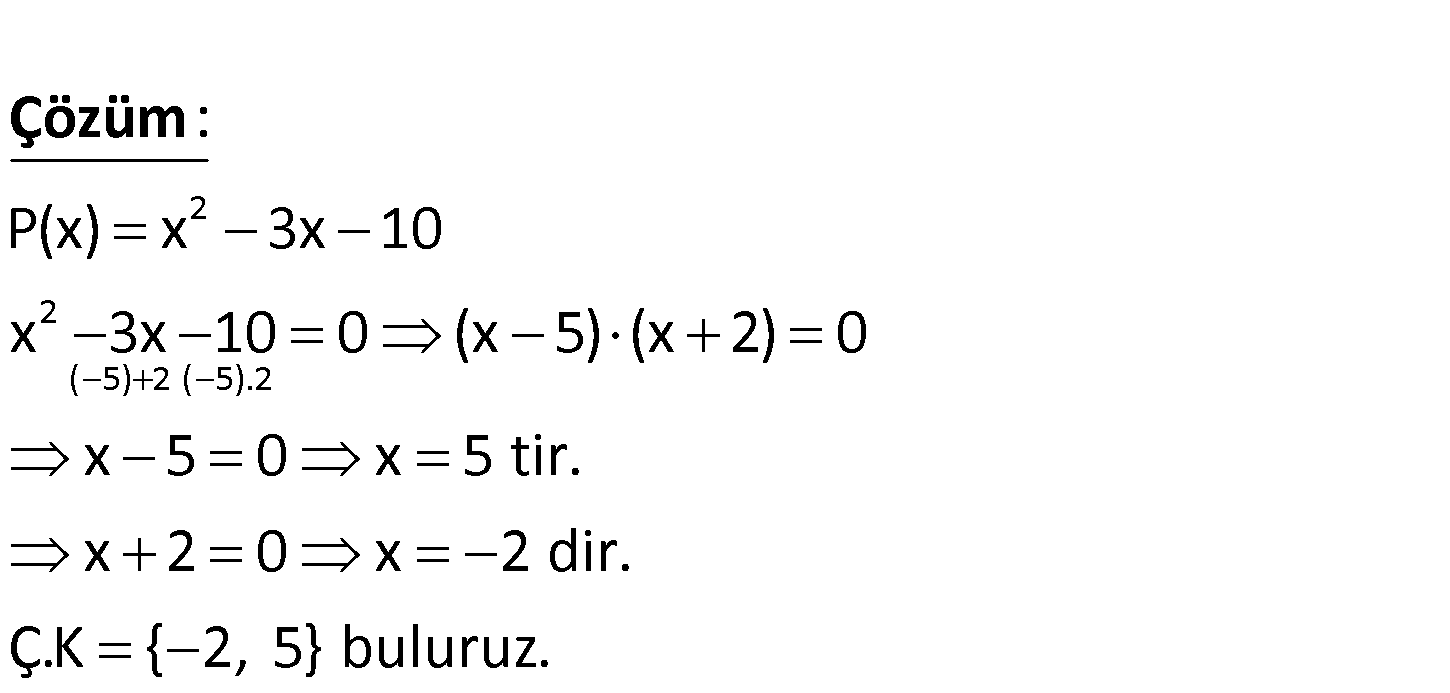
5.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net P x bir polinom olmak üzere, P x 0 denkleminin köklerine P x polinomunun sıfırları denir. m ve n birer 2 rasyonel sayı olmak üzere, P x x mx 2n polinomunun sıfırlarından biri 1 3 olduğuna göre, m n toplamı kaçtır? A) 0 B) 1 C) 2 D) 3 E) 5 2 Köklerinden biri 1 3 ise Diğer kökü bunun eşleniği olmalıdır. 1 3 x mx n in katsayıları : r Çözüm eel olduğu için Kökler toplamı: 1 3 1 3 2 dir. m 2 m 2 dir. 1 Kökler çarpımı: 1 3 1 3 1 3 2 dir. 2n 2 n 1 dir. 1 O halde; m n 2 1 3 buluruz. www.matematikkolay.net 76
P x üçüncü dereceden bir polinom olmak üzere, P 3 P 2 P 4 0 ve P 1 2 olduğuna göre, P 0 kaçtı r? 5 4 2 1 A) B) C) 1 D) E) 3 3 3 3 www.matematikkolay.net P( 3) P( 2) P(4) 0 ise P(x) polinomu x 3, x 2, x 4 çarpanlarına tam bölünür. P(x) de üçün : Çözüm cü dereceden bir polinom olduğuna göre; P(x) A(x 3)(x 2)(x 4) şeklinde yazabiliriz. P(1) 2 yi kullanarak A’yı bulalım. P(1) A.(4).(3).( 3) 2 1 A.( 36) 2 A dir. 18 1 P(x) (x 3)(x 2)(x 4) 18 P(0) 1 24 4 (3)(2)( 4) buluruz. 18 18 3 93
2 P x 3x ax 2 polinomunun bir sıfırı 2 olduğuna göre, a nın değerini bulunuz. www.matematikkolay.net 2 2 P(x) 0 x polinomun sıfırıdır. P(2) 0 dır. P(x) 3x ax 2 P(2) 3.2 a.2 2 0 12 2 2a 0 14 2a a 7 b : Çözüm uluruz. 113
2 P x x 3x 10 polinomunun sıfırlarını bulunuz. 2 2 ( 5) 2 ( 5).2 P(x) x 3x 10 x 3x 10 0 (x 5) (x 2) 0 x 5 0 x 5 tir. x 2 0 x 2 dir. Ç.K { : 2, 5} Çözüm buluruz. 114
2 P x x ax b polinomunun tam sayı sıfırları 3 ve 4 olduğuna göre a b toplamını bulunuz. 2 P(x) x ax b 0 denkleminin kökleri; x 3 ve x 4 ise P(x) (x 3).(x 4) şeklinde yazılabilir. P(x) : Çözüm 2 a b x 7x 12 dir. a b 7 12 5 buluruz. www.matematikkolay.net 121

