Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomun Derecesi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
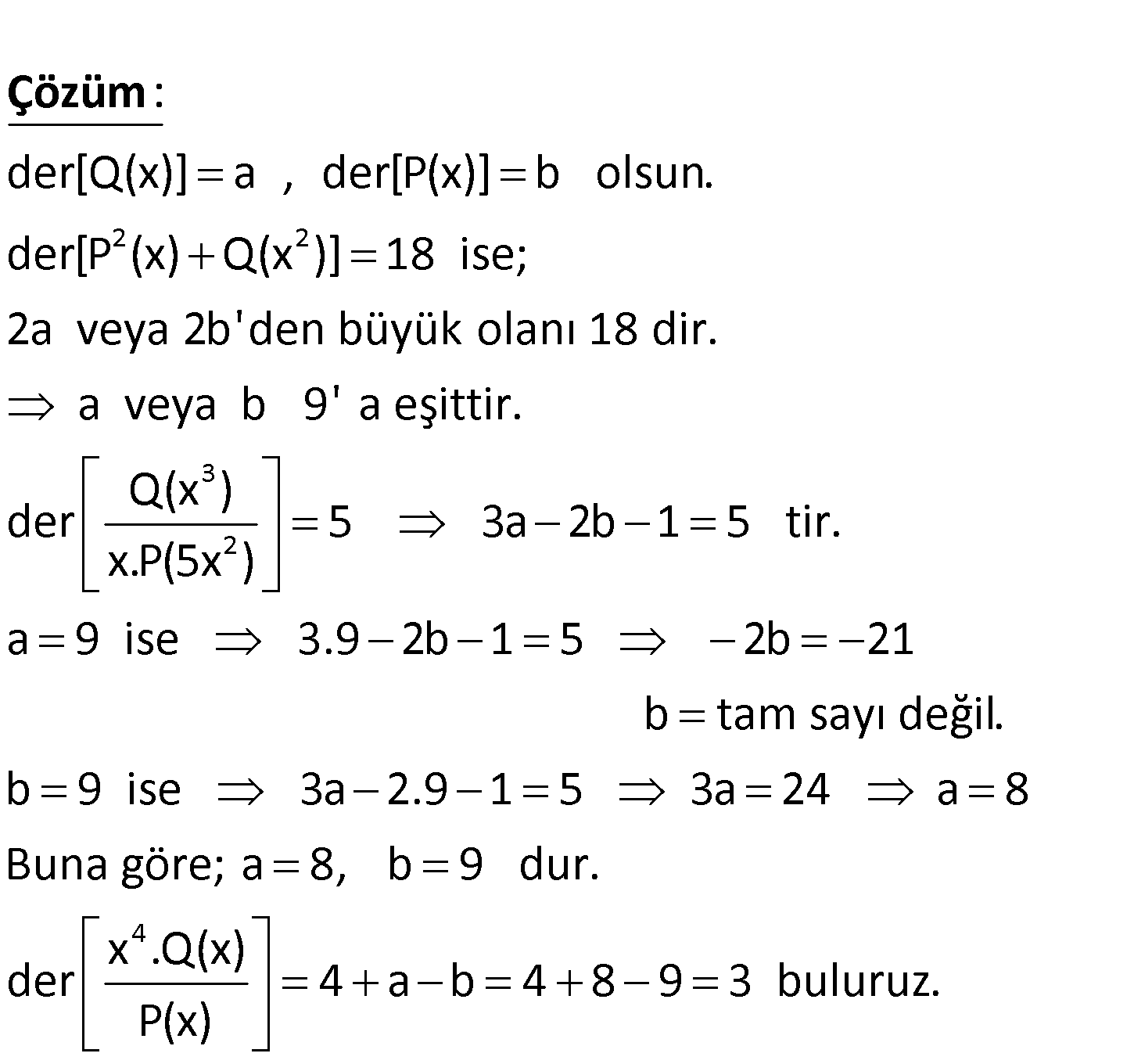
2.SORU


3.SORU


4.SORU
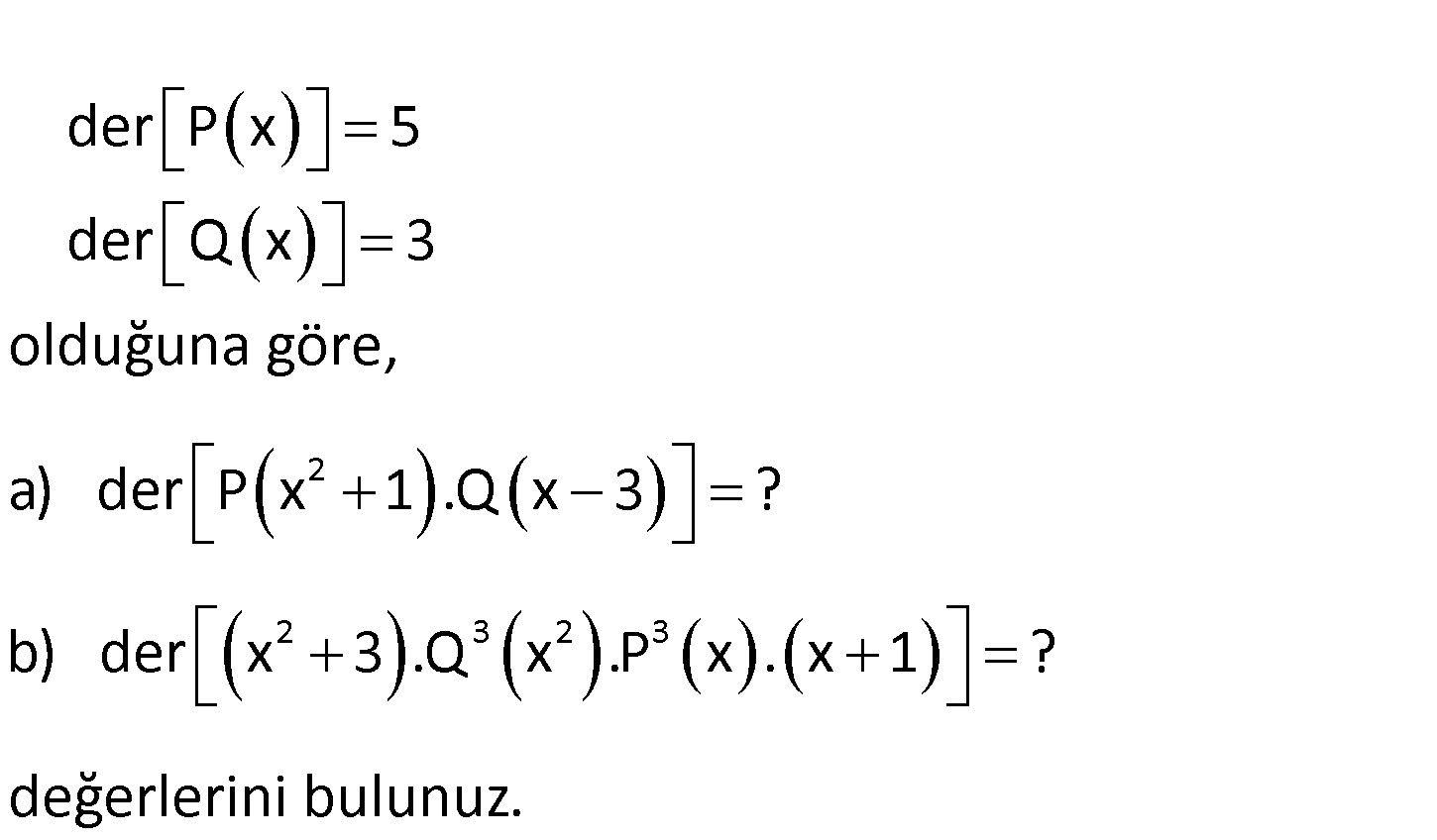
5.SORU
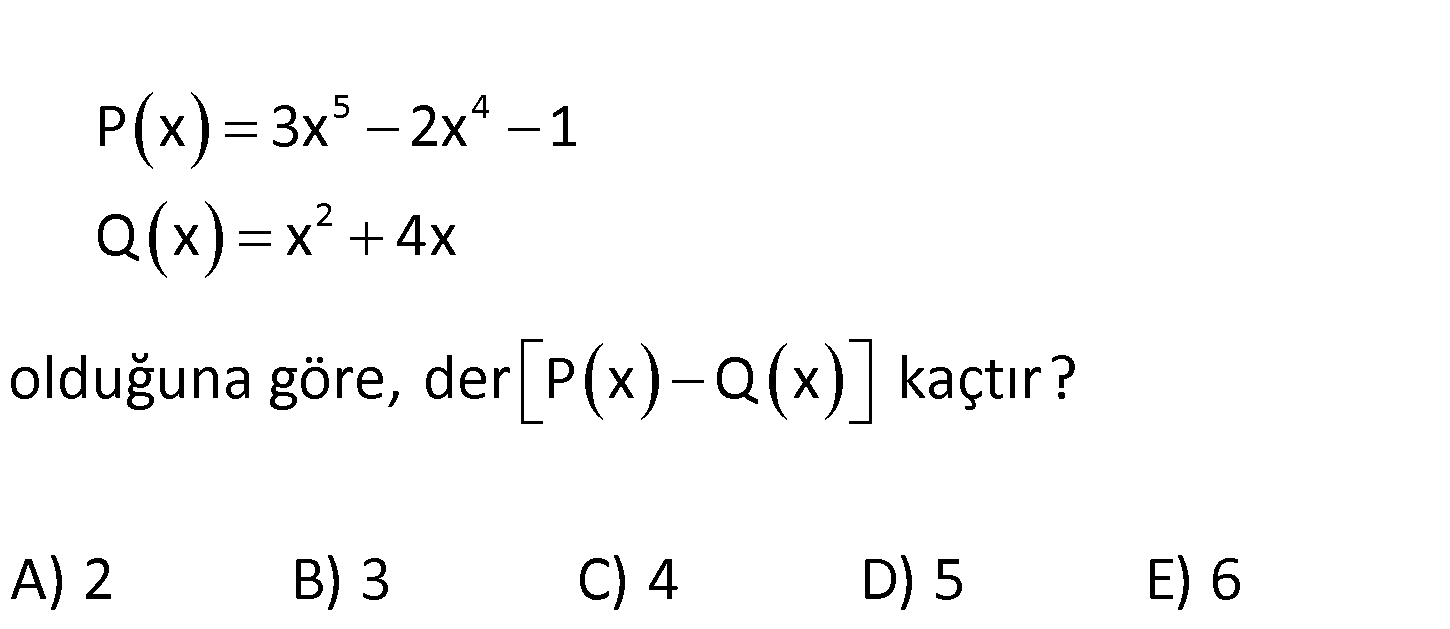
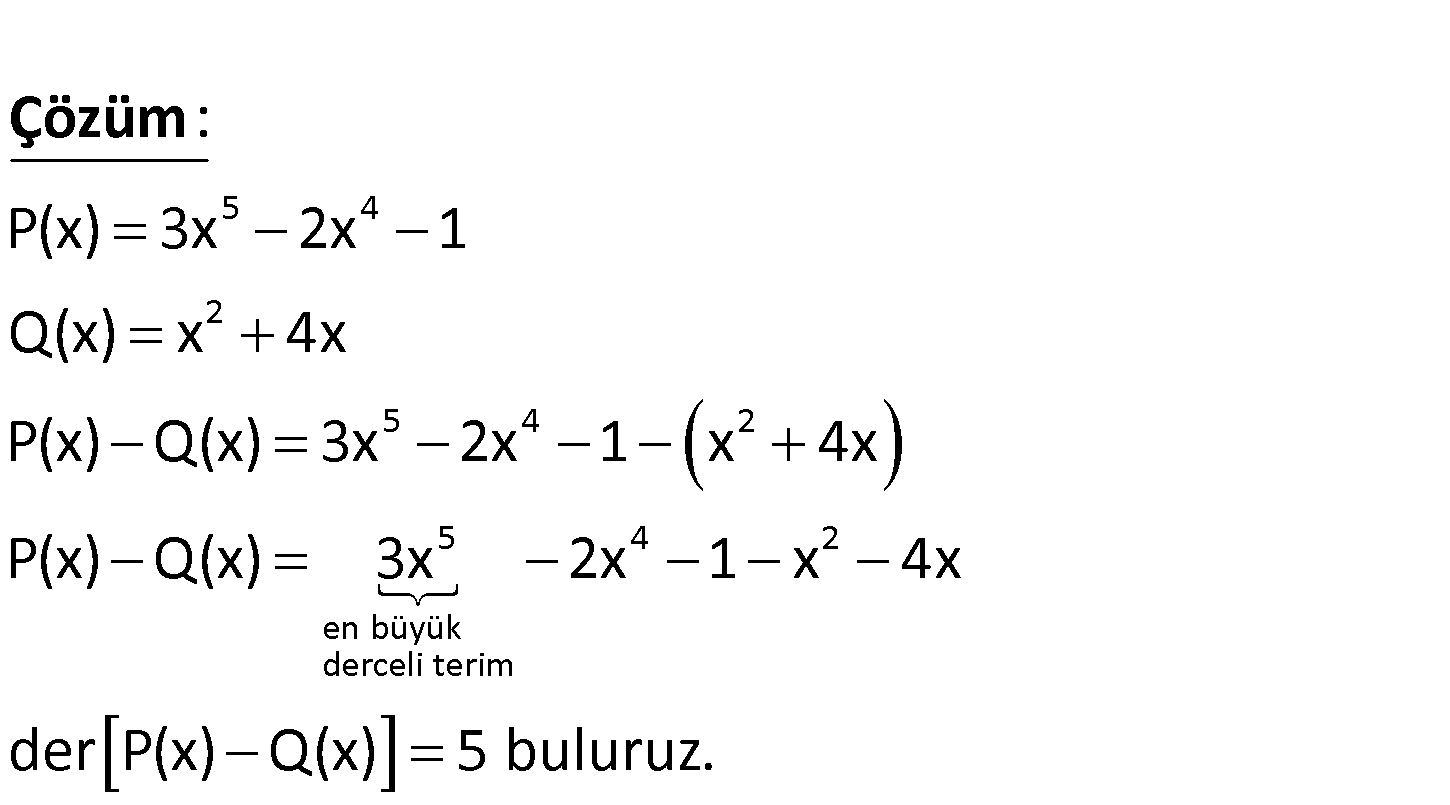
6.SORU


7.SORU


8.SORU


9.SORU
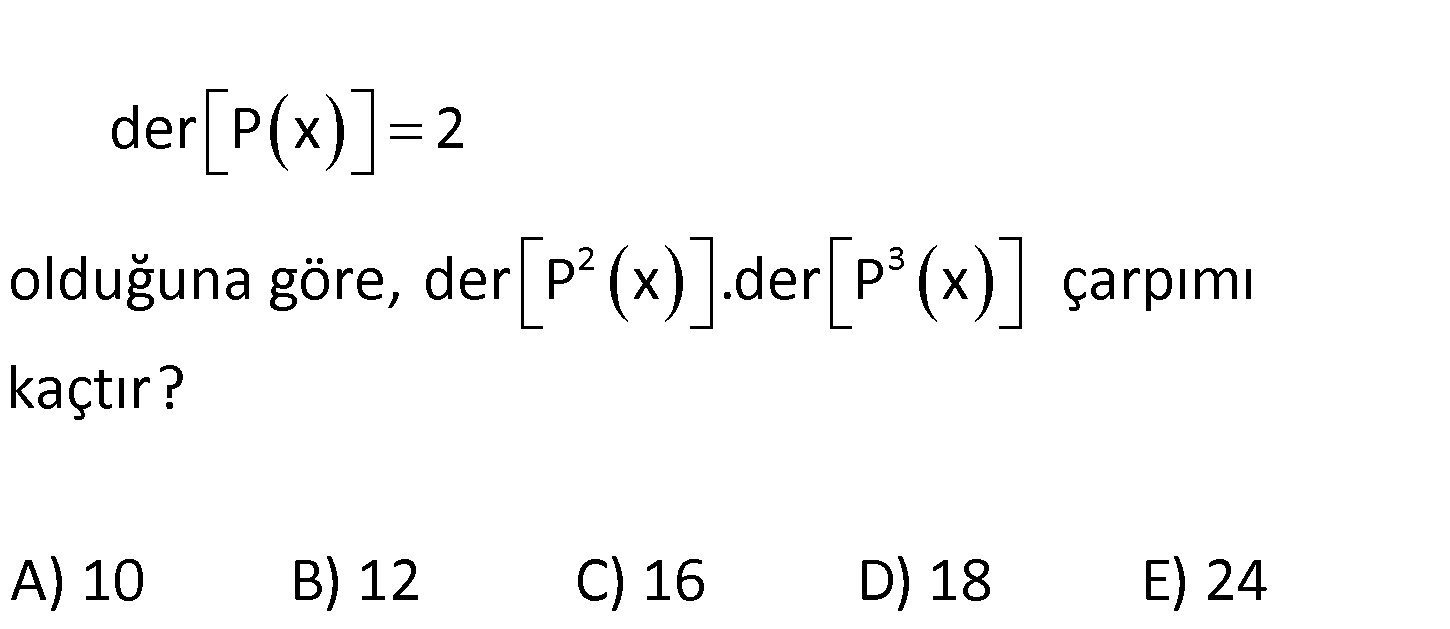
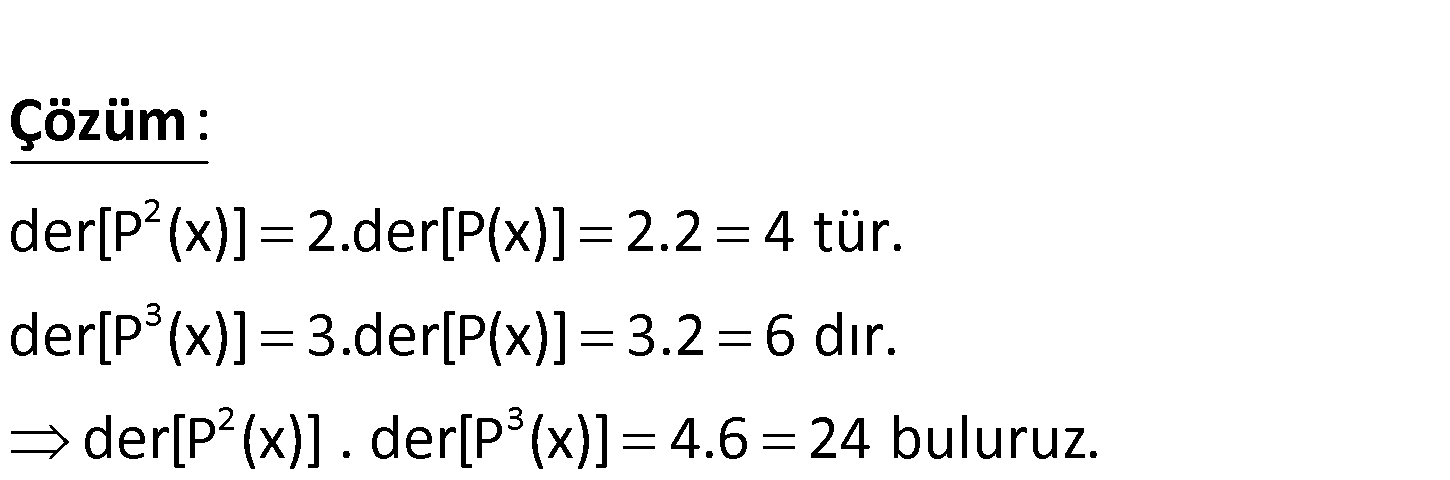
10.SORU
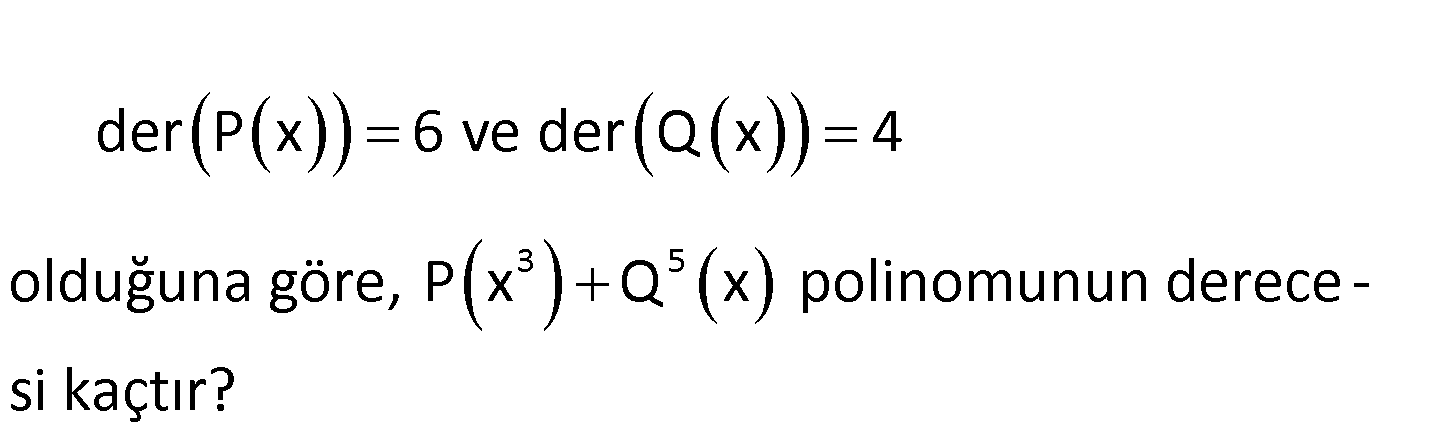

11.SORU
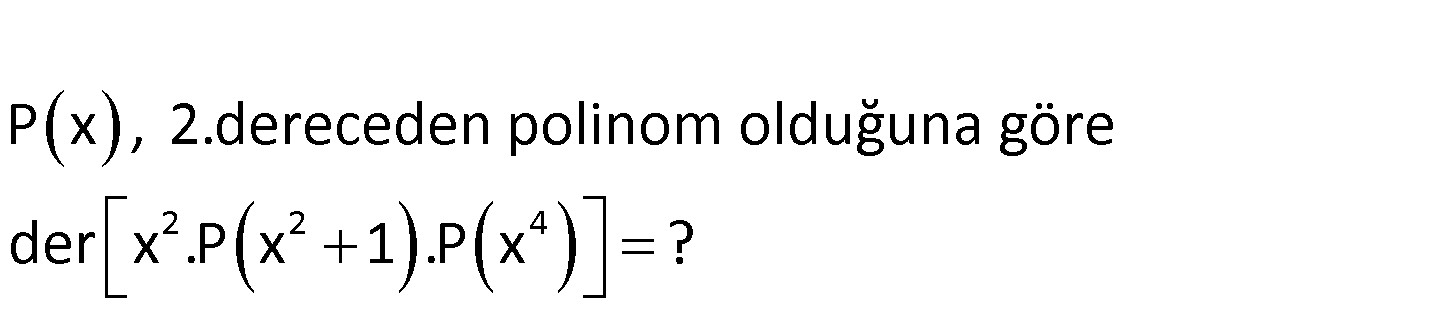

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
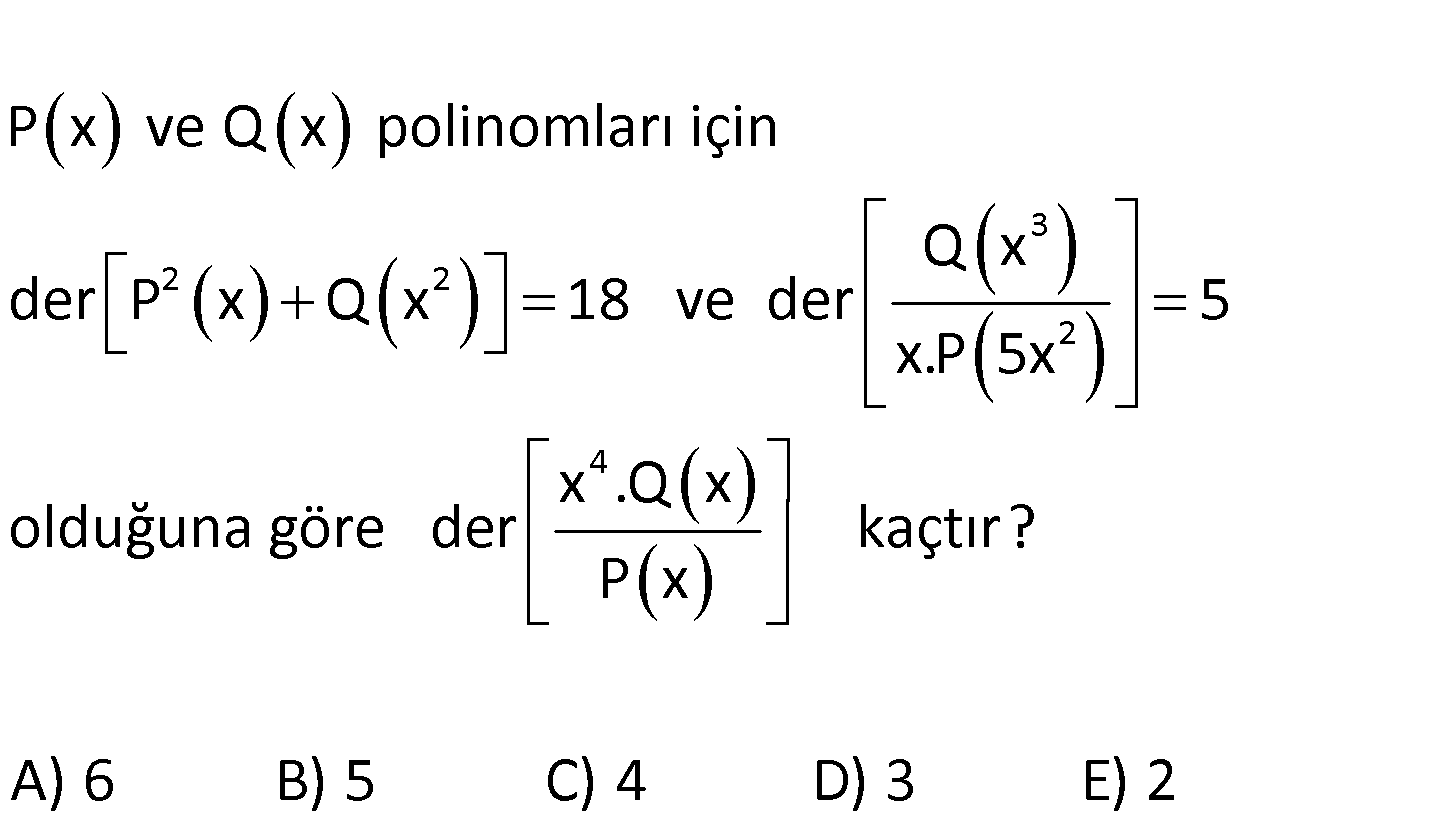
3 2 2 2 4 P x ve Q x polinomları için Q x der P x Q x 18 ve der 5 x.P 5x x .Q x olduğuna göre der P x kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 www.matematikkolay.net 2 2 der[Q(x)] a , der[P(x)] b olsun. der[P (x) Q(x )] 18 ise; 2a veya 2b’den büyük olanı 18 : Çözüm 3 2 dir. a veya b 9′ a eşittir. Q(x ) der 5 3a 2b 1 5 tir. x.P(5x ) a 9 ise 3.9 2b 1 5 2b 21 b tam sayı değil. b 9 ise 4 3a 2.9 1 5 3a 24 a 8 Buna göre; a 8, b 9 dur. x .Q(x) der 4 a b 4 8 9 3 buluruz. P(x) 4
P x ve Q x birer polinom olmak üzere, P x .Q x P x polinomun derecesi 6 ve polinomunun dere- Q x cesi 2 dir. 3 Buna göre, P 3x Q x 1 polinomunun derecesi kaçtır? A) 2 B) 4 C) 6 D) 8 E) 10 www.matematikkolay.net Çarpımda, der[P(x)] der[Q(x)] 6 Bölmede , der[P(x)] der[Q(x)] 2 taraf tarafa topl : a Çözüm 3 yınca 2der[P(x)] 8 der[P(x)] 4 tür. O halde; der[Q(x)] 2 dir. Buna göre; P(3x) Q(x 1) ün derecesi; x’in 3 le çarpılması dereceyi art 3 3 4.derece 3.2 6.derece tırmaz. Aynı kalır. x olması dereceyi 3 katına çıkarttırır. Buna göre; P(3x) Q(x 1) Polinomların toplamında hangisinin derecesi büyükse o alınır. Yani 6.derece Cevap: 6 36
3 2 2 P x , ikinci dereceden bir polinom olduğuna göre, P x 1 . P x x x çarpımı kaçıncı derec eden bir polinomdur? A) 12 B) 9 C) 8 D) 6 E) 5 www.matematikkolay.net 3 2 2 3 2 2 2.3 2.2 2 der P(x) 2 ise P(x 1). P(x) x x P(x 1). P(x) x x 6 4 2 12.derece Cevap: 12 : Çözüm 2 3 3 2 6 2 2 2 4 2 Bunu göremediysek, P(x) x varsayabiliriz. P(x 1) x 1 x … 6.derecedir. P(x) x x 4.derecedir. x x 2.derecedir. Bu üçü çarpıldığı için, dereceleri toplanır. 6 4 2 12 olur. 59
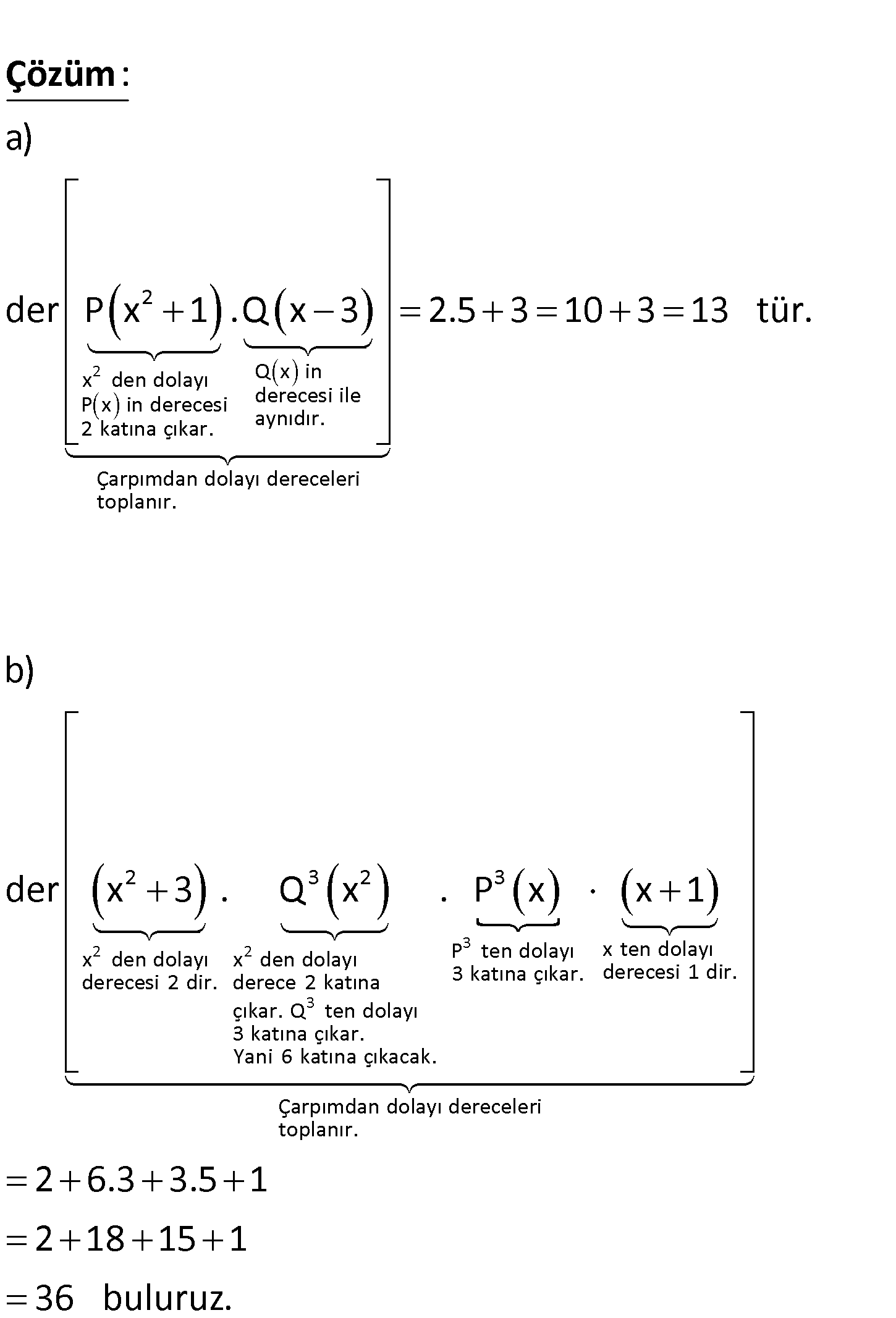
2 2 3 2 3 der P x 5 der Q x 3 olduğuna göre, a) der P x 1 .Q x 3 ? b) der x 3 .Q x P x . x 1 ? değerlerini bulunuz. www.matematikkolay.net 2 2 x den dolayı Q x in P x in derecesi derecesi ile 2 katına çıkar. aynıdır. a) der P x 1 .Q x : 3 Çözüm 2 2 3 Çarpımdan dolayı dereceleri toplanır. 2 3 2 x den dolayı x den dolayı derecesi 2 dir. derece 2 katına çıkar. Q ten dolayı 3 katına çıkar. Yani 6 kat 2.5 3 10 3 13 tür. b) der x 3 . Q x 3 3 P ten dolayı x ten dolayı 3 katına çıkar. derecesi 1 dir. ına çıkacak. Çarpımdan dolayı dereceleri toplanır. . P x x 1 2 6.3 3.5 1 2 18 15 1 36 buluruz. 81
5 4 2 P x 3x 2x 1 Q x x 4x olduğuna göre, der P x Q x kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 5 4 2 5 4 2 5 4 2 en büyük derceli terim P(x) 3x 2x 1 Q(x) x 4x P(x) Q(x) 3x 2x 1 x 4x P(x) Q(x) : 3x 2x 1 x Çözüm 4x der P(x) Q(x) 5 buluruz. www.matematikkolay.net 107
3 2 der P x =4 ve der Q x 3 olduğuna göre, der P x .Q x kaçtır? 3 2 3 2 3 der(P(x)) 4 der(P (x)) 3.4 12 dir. der(Q(x)) 3 der(Q(x )) 2.3 6 dır. der(P (x).Q(x )) der : (P (x Çözüm 2 3 2 )) der(Q(x )) der(P (x).Q(x )) 12 6 18 buluruz. 108
www.matematikkolay.net 3 4 2:00 AM a bir sayma sayısı olmak üzere, P x x x 5 Q x 3x 1 olduğuna göre, P x polinomunun Q x p olinomu ile bölümünden elde edilen bölüm polinomunun derecesinin alabileceği değerler toplamı kaçtır? der[P(x)] 3.4 12 dir. der[Q(x)] 2a P(x) der 12 2a dır. Q(x) a 1,2,3,… olduğund : an; 12 2a Çözüm 10,8,6,4,2,0 değerlerini alabilir. Bu değerlerin toplamı; 10 8 6 4 2 0 30 bulunur. 19
3 2 P x x x Q x x 1 oduğuna göre, P x ve Q x polinomlarının en büyük ortak bölen ve en küçük ortak kat poli nomlarının çarpımının derecesi kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 3 2 3 P(x) x x Q(x) x 1 ebob(P(x),Q(x)).ekok(P(x),Q(x)) P(x).Q(x) tir. der[P(x).Q(x)] der[P(x) : ] Çözüm 1 der[Q(x)] tir. der[P(x).Q(x)] 3 1 4 bulunur. 21
2 3 der P x 2 olduğuna göre, der P x .der P x çarpımı kaçtır? A) 10 B) 12 C) 16 D) 18 E) 24 2 3 2 3 der[P (x)] 2.der[P(x)] 2.2 4 tür. der[P (x)] 3.der[P(x)] 3.2 6 dır. der[P (x)] . der[P (x)] : 4 Çözüm .6 24 buluruz. 120
www.matematikkolay.net 3 5 der P x 6 ve der Q x 4 olduğuna göre, P x Q x polinomunun derece – si kaçtır? 3 5 der[P(x)] 6 der[P(x )] 3.6 18 dir. der[Q(x)] 4 der[Q (x )] 5.4 20 dir. Not : İki polinom topla d : n Çözüm 3 5 18 20 ığında veya çıkartıldığında polinomun derecesi, derecesi büyük olan polinomun derecesine eşittir. der[P(x )Q (x )] 20 buluruz. 128
2 2 4 P x , 2.dereceden polinom olduğuna göre der x .P x 1 .P x ? 2 2 4 2 2 4 der[x .P(x 1).P(x )] der[x ] der[P(x 1)] der[P(x )] 2 2.der[P(x)] 4.der[P(x)] : 2 2.2 4.2 2 Çözüm 4 8 14 buluruz. 145


ironik bir isim olmuş
4. B çözümünde hata yapîlmış. Çözümde toplama işlemi çarpma olarak alınmış.
Uyarınız için teşekkürler. Soruda yazım hatası yapılmış. Şimdi düzeltildi.