Soru Sor sayfası kullanılarak Polinomlar konusu altında Polinomların eşitliği ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

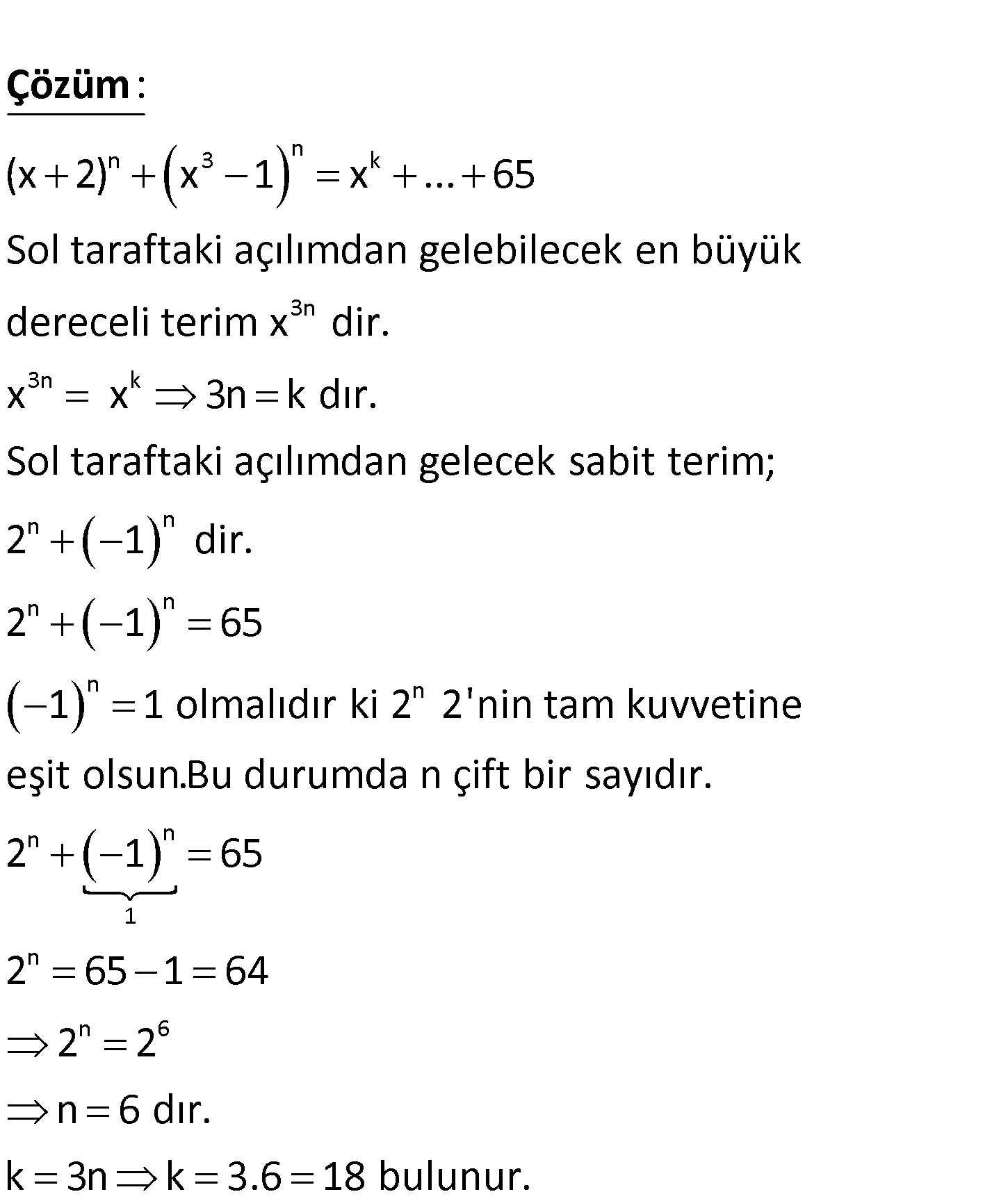
2.SORU


3.SORU
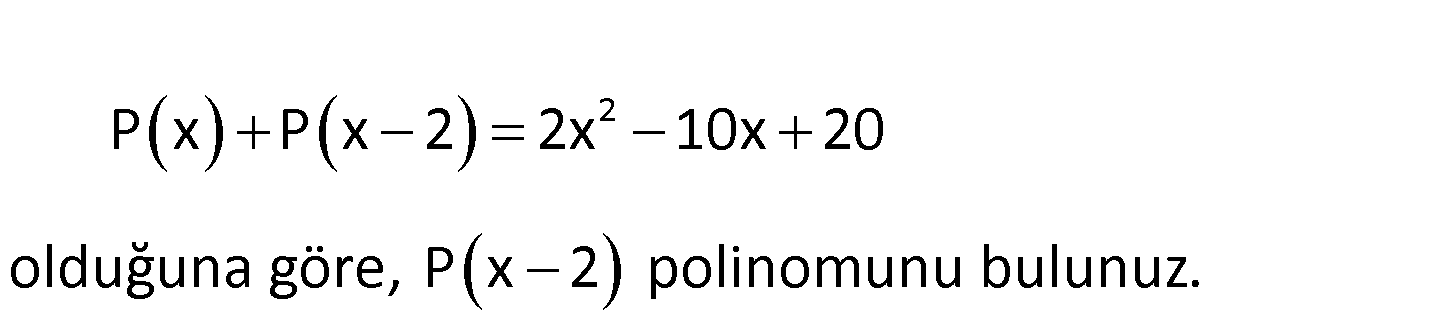

4.SORU
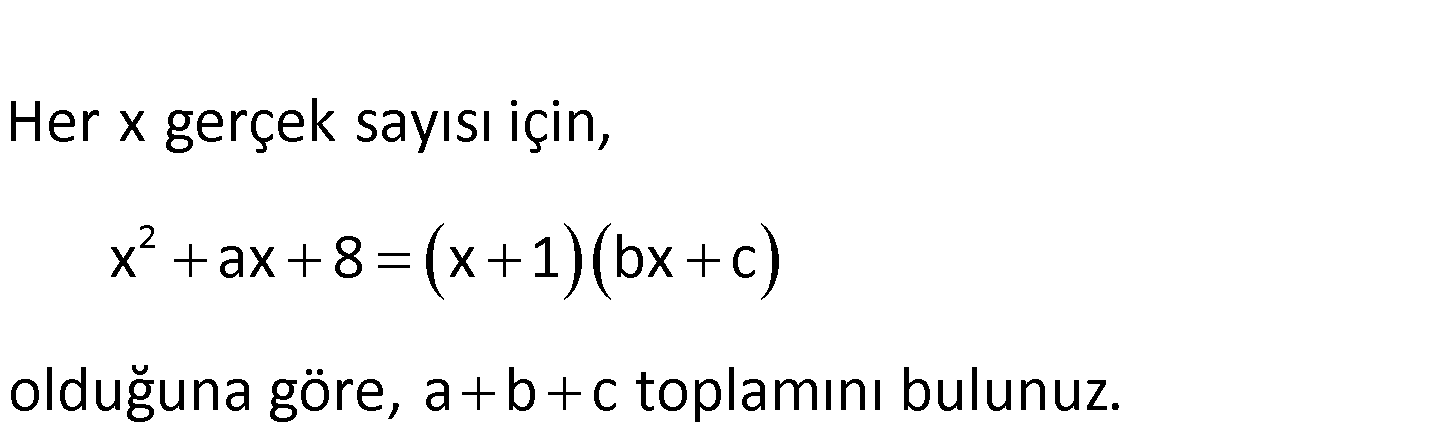

5.SORU
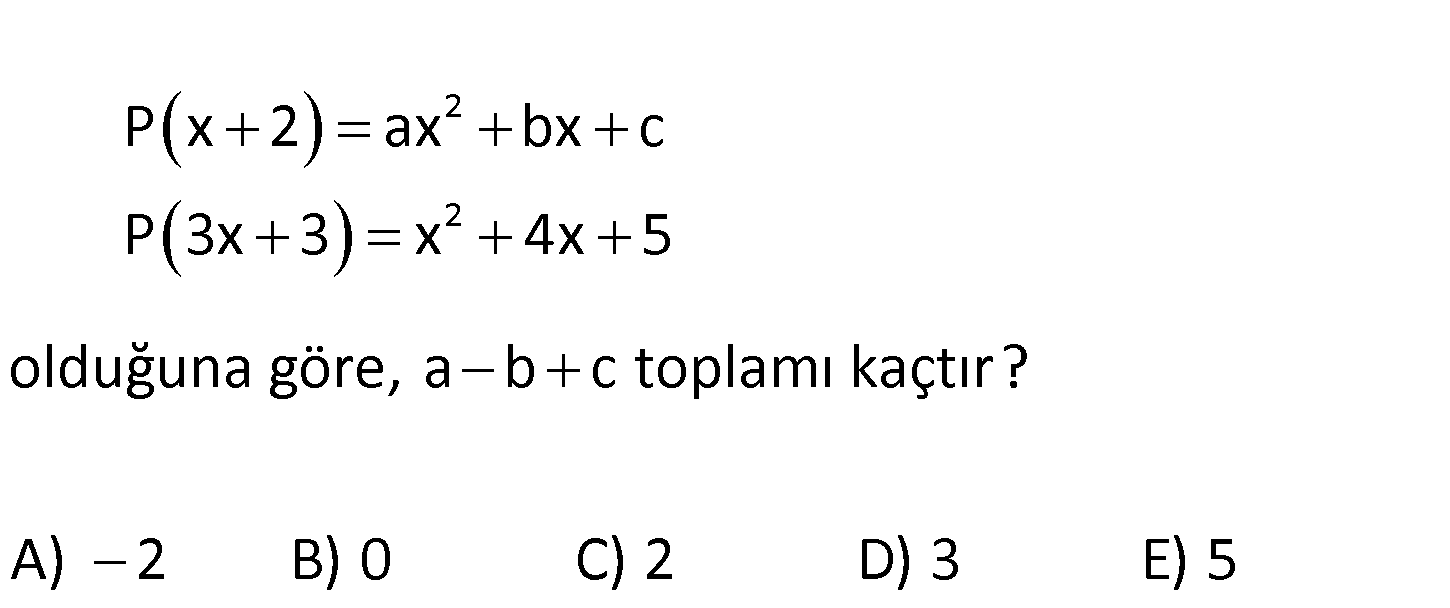

6.SORU

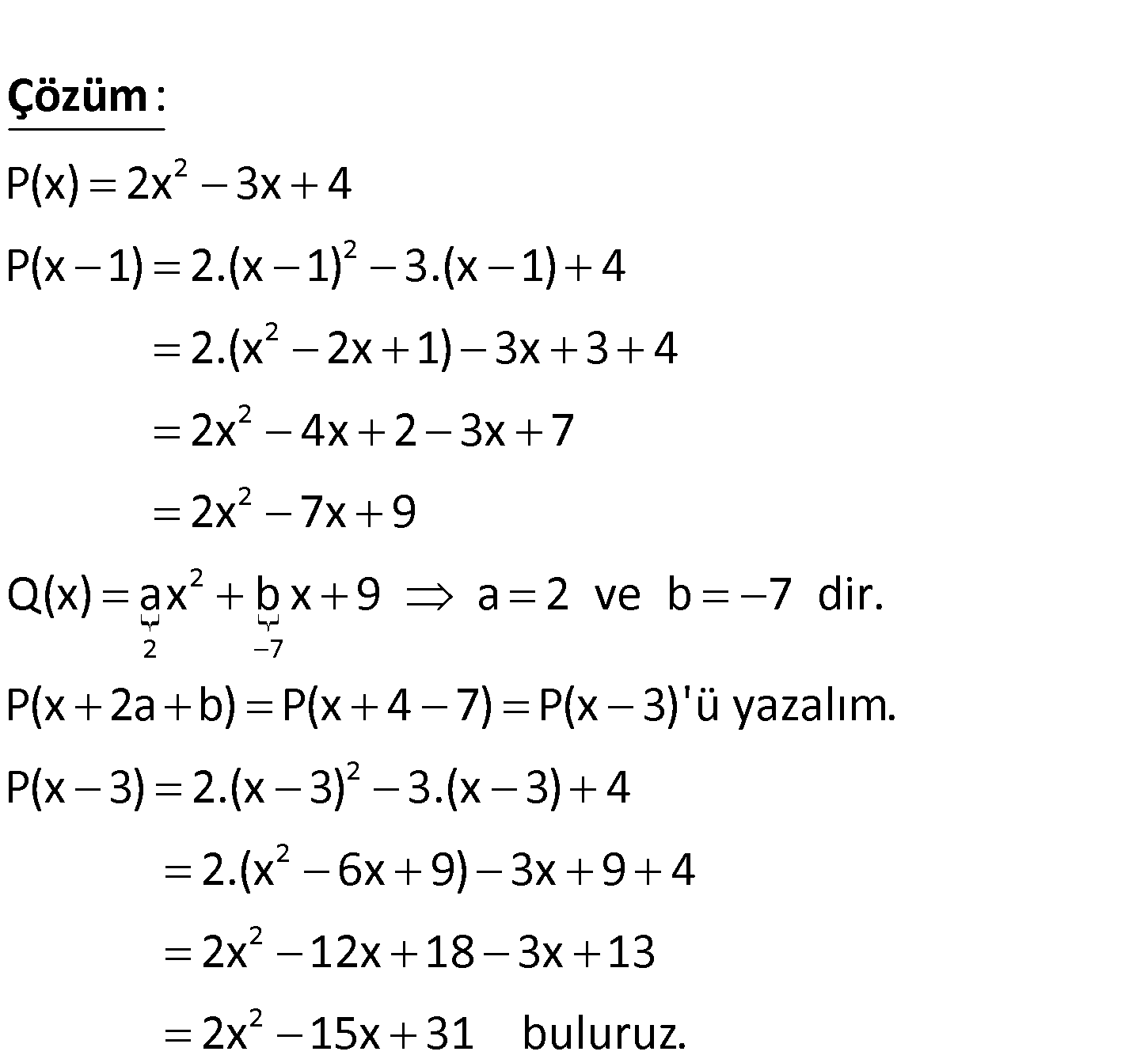
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
n 3 n k k x 2 x 1 x … 65 özdeşliğinde x en büyük dereceli terim olduğuna göre, k kaçtır? A) 6 B) 12 C) 15 D ) 18 E) 24 n 3 n k 3n (x 2) x 1 x … 65 Sol taraftaki açılımdan gelebilecek en büyük dereceli terim x dir. x : Çözüm 3n k n n n n n n n n 1 n n 6 x 3n k dır. Sol taraftaki açılımdan gelecek sabit terim; 2 1 dir. 2 1 65 1 1 olmalıdır ki 2 2’nin tam kuvvetine eşit olsun.Bu durumda n çift bir sayıdır. 2 1 65 2 65 1 64 2 2 n 6 dır. k 3 nk 3.6 18 bulunur. 26
n 3 n k k x 2 x 1 x … 65 Özdeşiliğinde x en büyük dereceli terim olduğuna göre, k kaçtır? A) 6 B) 12 C) 15 D) 18 E) 24 www.matematikkolay.net n 3 n k n n (x 2) (x 1) x … 65 Sabit terimlerin toplamı 65 olmalıdır. 2 ( 1) 65 n 6 olur e : sa ş Çözüm 6 6 3 6 18 k 18 itlik sağlanır. (x 2) en büyük dereceli terim x dır. (x 1) en büyük dereceli terim x dir. Buna x x dir k 18 buluruz. 87
2 P x P x 2 2x 10x 20 olduğuna göre, P x 2 polinomunu bulunuz. 2 P(x 2) polinomu ax bx c olsun. P(x) P(x 2 2) olduğundan ilk polinomda x yerine x 2 yazalım. : P Çözüm 2 2 2 2 2 2 2 2 (x) a(x 2) b(x 2) c P(x) ax 4ax 4a bx 2b c P(x) P(x 2) ax bx c ax 4ax 4a bx 2b c P(x) P(x 2) 2ax (4a 2b)x 4a 2b 2c P(x) P(x 2) 2x 10x 20 2ax (4a 2b)x 4a 2b 2c 2x 10x 20 Buradan aynı kuvvetli teriml 2 erin katsayılarını eşitleyelim 2a 2 a 1 dir. 4a 2b 10 4 2b 10 2b 14 b 7 dir. 4a 2b 2c 20 4 14 2c 20 2c 30 c 15 dir. Buradan P(x 2) x 7x 15 bulunur. 122
2 Her x gerçek sayısı için, x ax 8 x 1 bx c olduğuna göre, a b c toplamını bulunuz. 2 2 2 2 2 x ax 8 (x 1)(bx c) (sağ tarafı açalım) x ax 8 bx cx bx c x ax 8 bx (c b)x c (Aynı kuvvet : Çözüm 2 2 li ifadelerin katsayılarını eşitleyelim.) c 8 x bx b 1 dir. ax (c b)x a c b a 1 8 9 dur. a b c 9 1 8 18 buluruz. 129
www.matematikkolay.net 2 2 P x 2 ax bx c P 3x 3 x 4x 5 olduğuna göre, a b c toplamı kaçtır? A) 2 B) 0 C) 2 D) 3 E) 5 2 2 P(x 2) ax bx c P(2x 3) x 4x 5 İki polinomun içerisi birbirine eşitleyelim. 2x 3 x 2 x 1 Şim : d Çözüm 2 2 i bu x değerini iki polinomda da yerine yazalım. P( 1 2) a( 1) b( 1) c P(1) a b c dir. Şimdi diğer polinoma bakalım P(2.( 1) 3) ( 1) 4( 1) 5 P(1) 1 4 5 2 dir. Buradan; a b c 2 buluruz. 99
2 2 P x 2x 3x 4 Q x ax bx 9 olmak üzere, P x 1 Q x olduğuna göre, P x 2a b polinomunun eşiti aşağıdakilerde 2 2 2 2 2 n hangisidir? A) 2x 13x 29 B) 2x 14x 30 C) 2x 15x 31 D) 2x 16x 32 E) 2x 17x 33 2 2 2 2 P(x) 2x 3x 4 P(x 1) 2.(x 1) 3.(x 1) 4 2.(x 2x 1) 3x 3 4 2x 4x 2 3 : Çözüm 2 2 2 7 2 2 2 x 7 2x 7x 9 Q(x) ax b x 9 a 2 ve b 7 dir. P(x 2a b) P(x 4 7) P(x 3)’ü yazalım. P(x 3) 2.(x 3) 3.(x 3) 4 2.(x 6x 9) 3x 9 4 2x 12x 18 3x 13 2 x2 15x 31 buluruz. 149

