Soru Sor sayfası kullanılarak Polinomlar konusu altında Kolay Polinom Soruları, Kısa Polinom Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
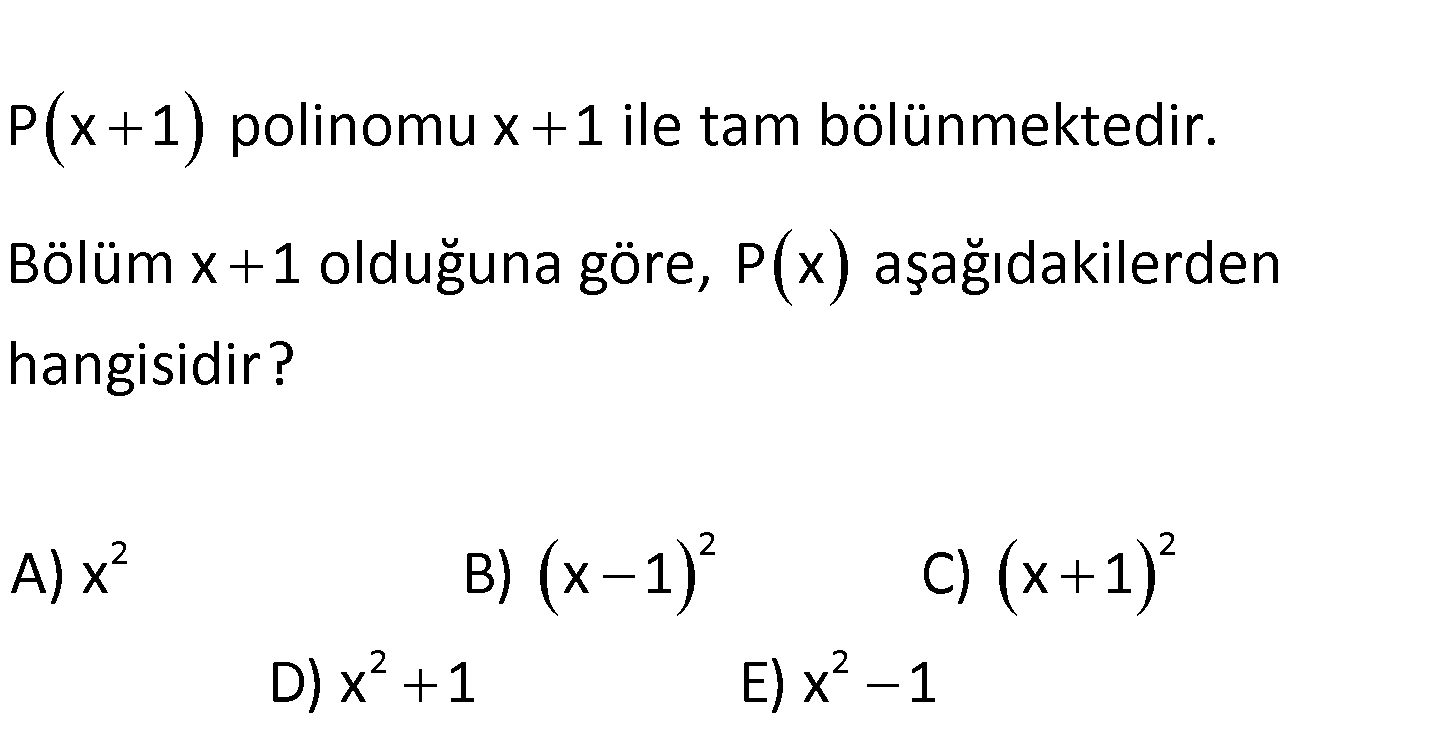

2.SORU


3.SORU


4.SORU


5.SORU


6.SORU


7.SORU


8.SORU
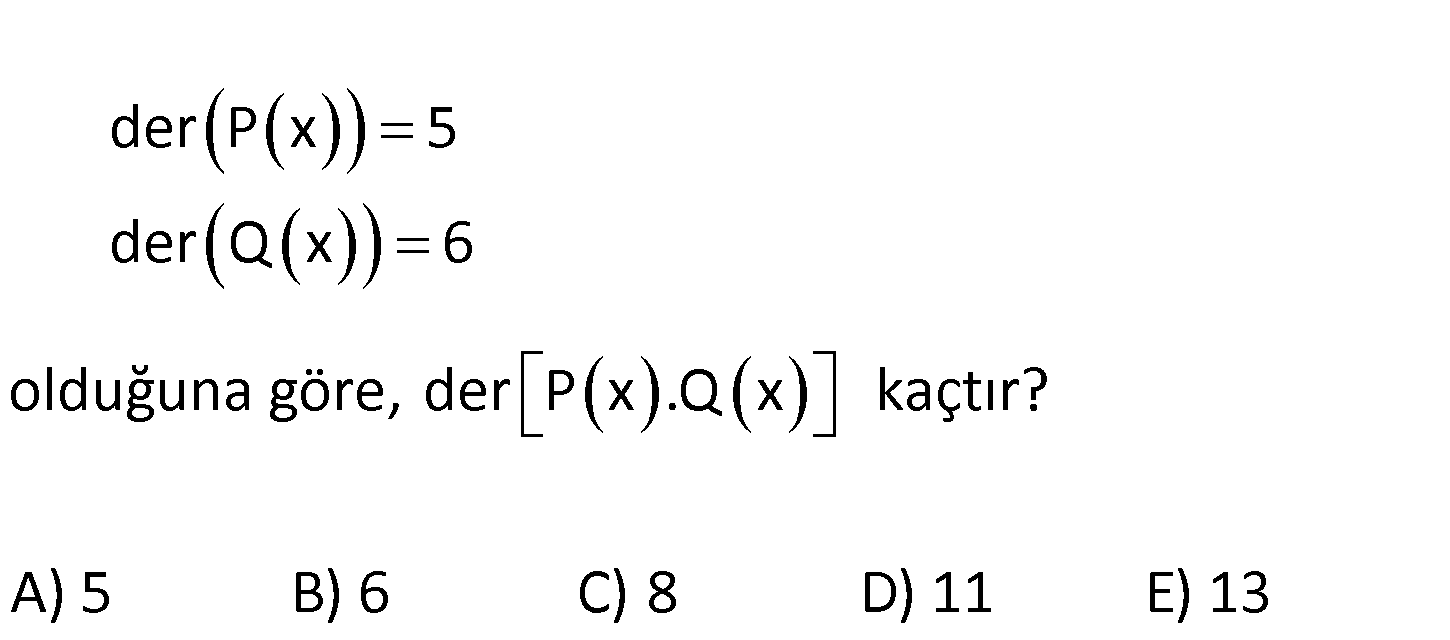
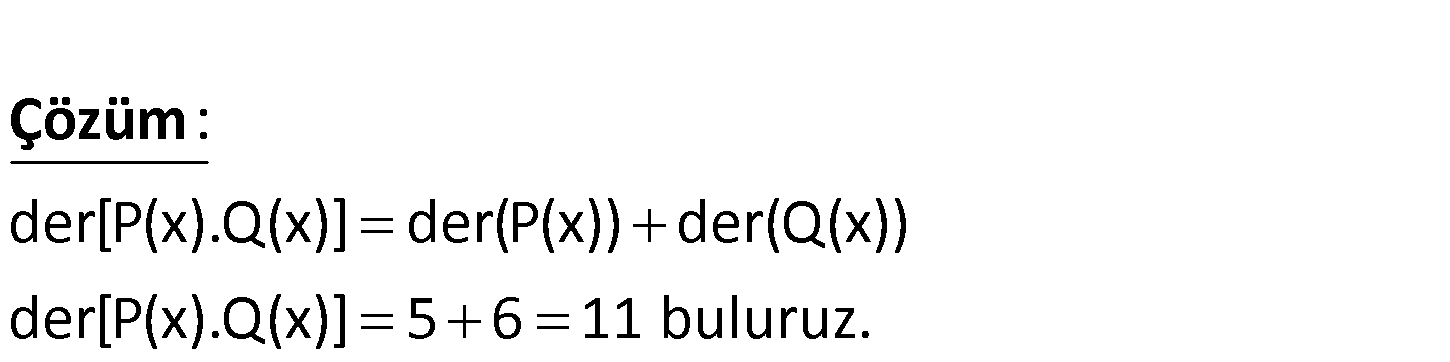
9.SORU
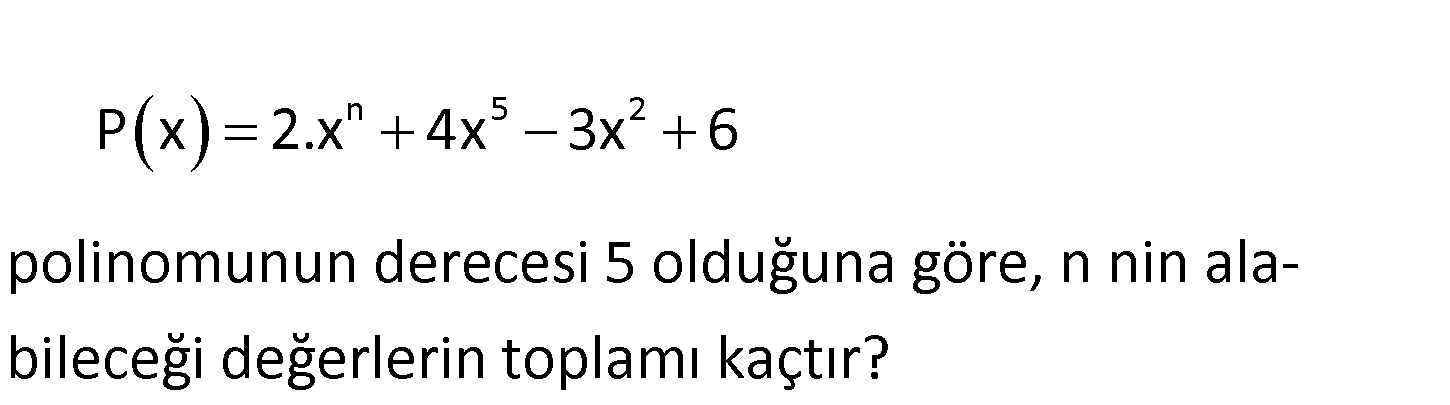

10.SORU
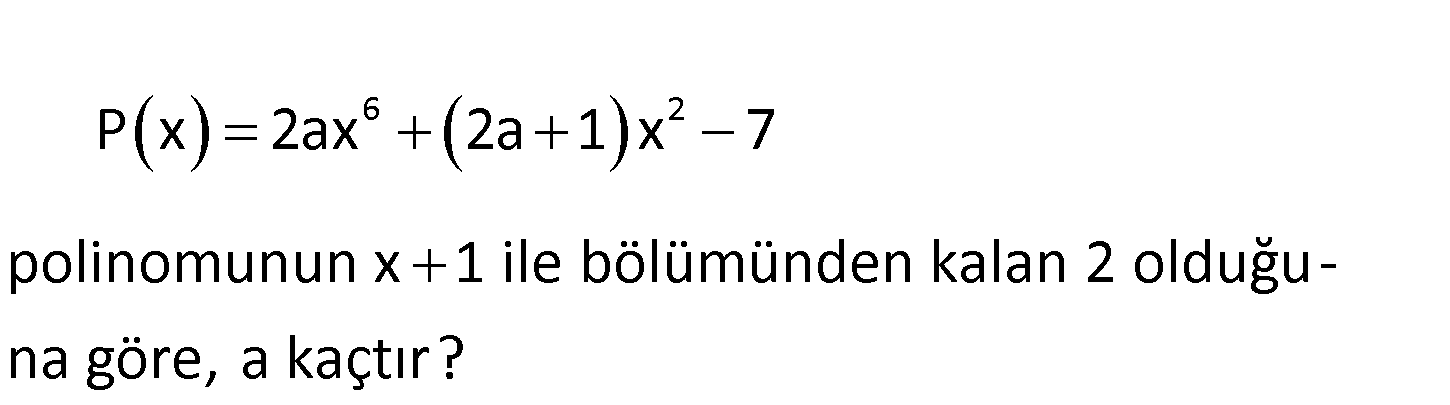
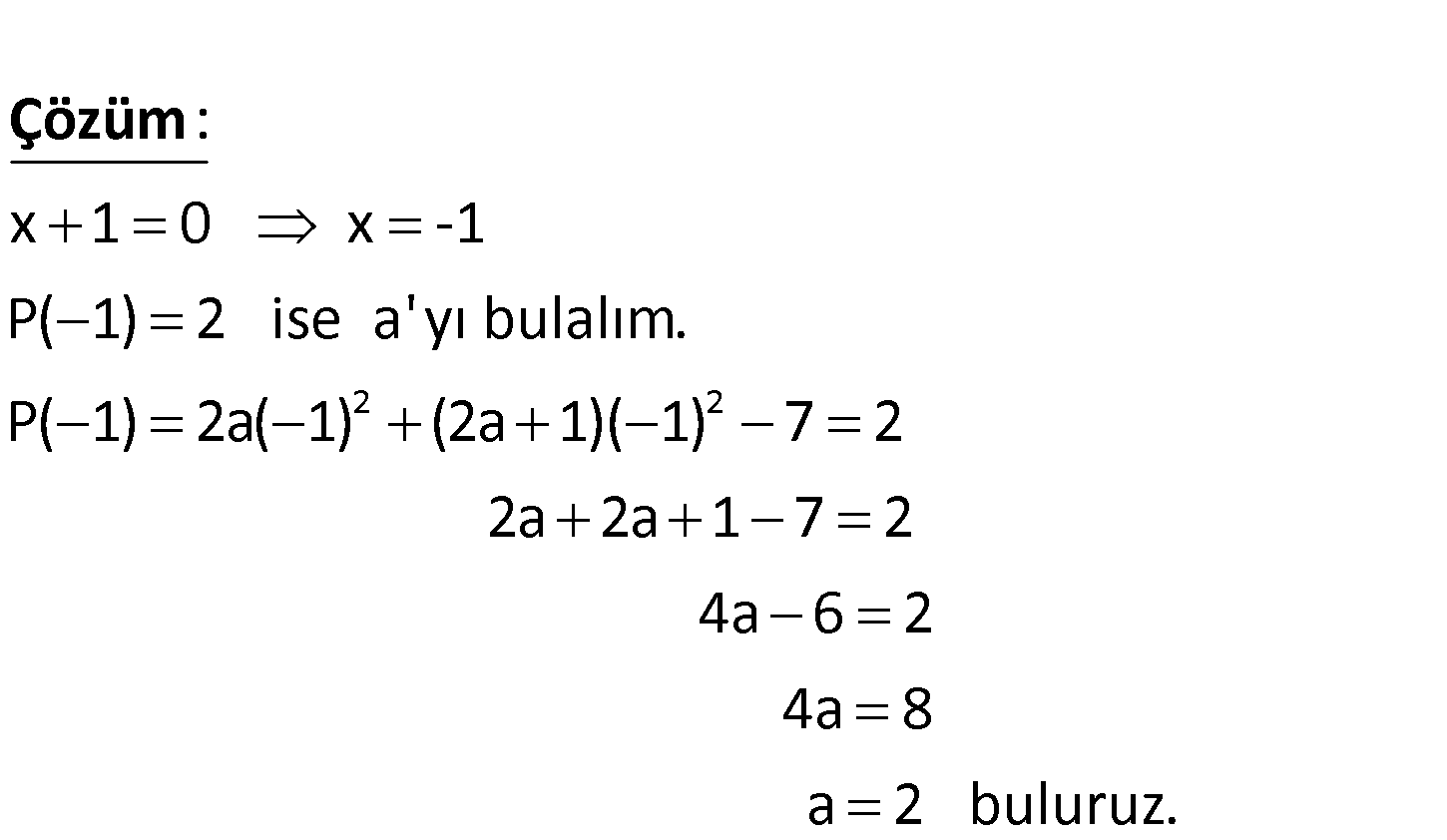
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net P x 1 polinomu x 1 ile tam bölünmektedir. Bölüm x 1 olduğuna göre, P x aşağıdakilerden hangisidir? A) x 2 2 2 2 2 B) x 1 C) x 1 D) x 1 E) x 1 P x 1 x 1 x 1 0 Böyle ise P(x 1) x 1 x 1 dir. P(x 1) : x Çözüm 2 2 1 Yani bu polinom, içerdeki ifadenin karesini alan bir polinomdur. O halde; P(x) x dir. 65
3 2 P x 3x x 4m veriliyor. P x polinomunun çarpanlarından biri x 1 olduğu – na göre, m kaçtır? www.matematikkolay.net x 1 çarpanlardan biri ise x 1 için tüm polinom 0 olur. Örneğin bu polinom P x x 1 Q x şeklind : Çözüm 3 2 1 1 edir. x 1 yazınca P 1 0.Q 1 0 oluyor. P 1 0 ise 3 x x 4m 0 3 1 4m 0 4 4m 0 4m 4 m 1 buluruz. 73
3 P x x 4x k 3 veriliyor. P x polinomunu x ile tam bölündüğüne göre, k kaçtır? 3 0 0 P(x) x.Q x ise x 0 için polinom 0 çıkar. Yani; P 0 0 dır. x 4x k 3 0 0 0 k 3 0 : Çözüm k 3 buluruz. www.matematikkolay.net 74
www.matematikkolay.net 2 P x x 4x 5a 1 polinomu x 1 ile bölündüğünde 4 kalanını veriyorsa, a kaçtır? A) 4 B) 2 C) 3 D) 1 E) 2 2 1 1 x 1 0 ‘a eşitleriz. x 1 dir. Demek ki P 1 4 tür. Buna göre; x 4x 5a 1 4 1 4 5 1 : a 4 6 Çözüm 5a 4 5a 10 a 2 buluruz. 78
3 x bir pozitif tamsayı olmak üzere bir bölme işleminde bölünen x 11, bölen x 2, kalan 3 tür. Buna 2 2 2 2 2 göre, bölüm aşağıdakilerden hangisidir? A) x 2 B) x 2 C) x 2x 2 D) x 4 E) x 2x 4 www.matematikkolay.net 3 3 x 11 sayısı x 2’ ye bölündüğünde 3 kalanını veriyorsa x 11’in 3 eksiği tam bölünmelidir. Y : a Çözüm 3 3 3 2 2 3 2 2 Bölen Bölüm 2 2 2 2 2 ni x 8 tam bölünüyordur. Not : a b (a b)(a ab b ) dir. Buna göre; x 8 (x 2)(x 2x 2 ) dir. Bu ifade (x 2)’ye bölündüğünde bölüm (x 2x 2 ) olur. (x 2x 2 ) x 2x 4 buluru z. Cevap: E 88
4 3 P x ax bx 3x 2 polinomunun katsayılar toplamı 5 olduğuna göre, a b toplamını bulunuz. 4 3 4 3 Polinomun katsayılar toplamı P(1) ile bulunur. P(x) ax bx 3x 2 P(1) 5 a.(1) b.(1) 3.1 2 : 5 Çözüm ab 523 4 buluruz. 101
www.matematikkolay.net 2 P x 18x 6x 10 polinomunun 3x 4 ile bölümünden elde edilen kalan kaçtır? 3x 4’ü 0 yapan x değerini bulalım. 4 3x 4 0 3x 4 x 3 Şimdi bu değer : i polinomda ku Çözüm 2 llanalım. 4 4 4 P 18 6 10 3 3 3 18 2 16 9 6 2 4 3 10 32 8 10 14 buluruz. 115
der P x 5 der Q x 6 olduğuna göre, der P x .Q x kaçtır? A) 5 B) 6 C) 8 D) 11 E) 13 der[P(x).Q(x)] der(P(x)) der(Q(x)) der[P(x).Q(x)] 5 6 11 buluruz. : Çözüm www.matematikkolay.net 119
n 5 2 P x 2.x 4x 3x 6 polinomunun derecesi 5 olduğuna göre, n nin alabileceği değerlerin toplamı kaçtır? n 5 2 P(x) 2x 4x 3x 6 polinomunun derecesi 5 olduğuna göre n’nin en büyük değeri 5 tir.Buna göre : Çözüm ; n {5,4,3,2,1,0} değerlerini alır. 5 4 3 2 1 0 15 buluruz. 124
www.matematikkolay.net 6 2 P x 2ax 2a 1 x 7 polinomunun x 1 ile bölümünden kalan 2 olduğu – na göre, a kaçtır? 2 2 x 1 0 x -1 P( 1) 2 ise a’yı bulalım. P( 1) 2a( 1) (2a 1)( 1) 7 2 : Çözüm 2a 2a 1 7 2 4a 6 2 4a 8 a 2 buluruz. 125


BU İŞLETMEDE EMEĞİ GEÇEN HERKESİN 🙂