Soru Sor sayfası kullanılarak Polinomlar konusu altında Katsayılar Toplamı, Sabit Terim ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
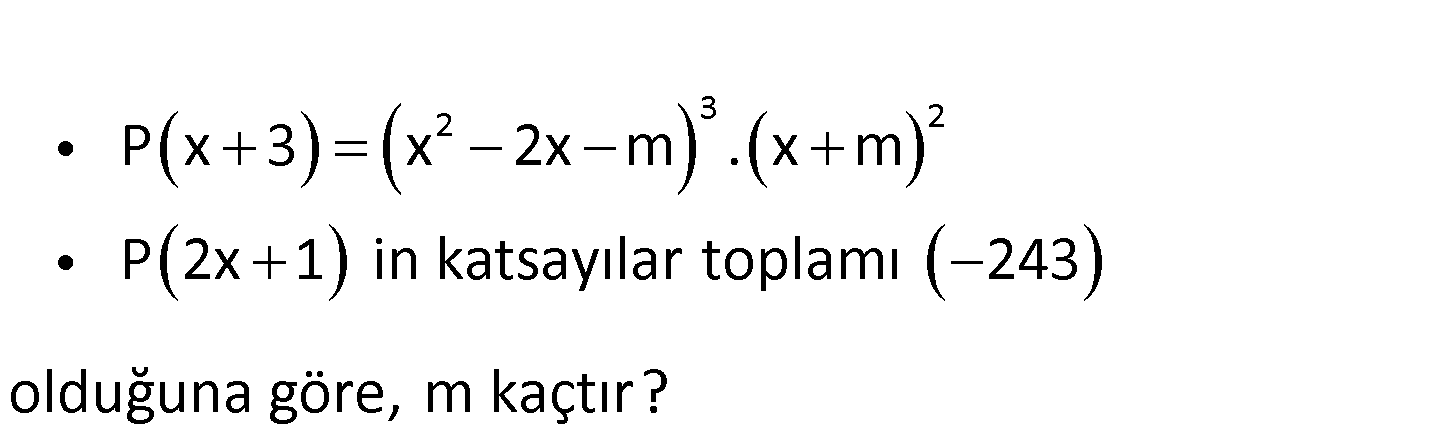

3.SORU
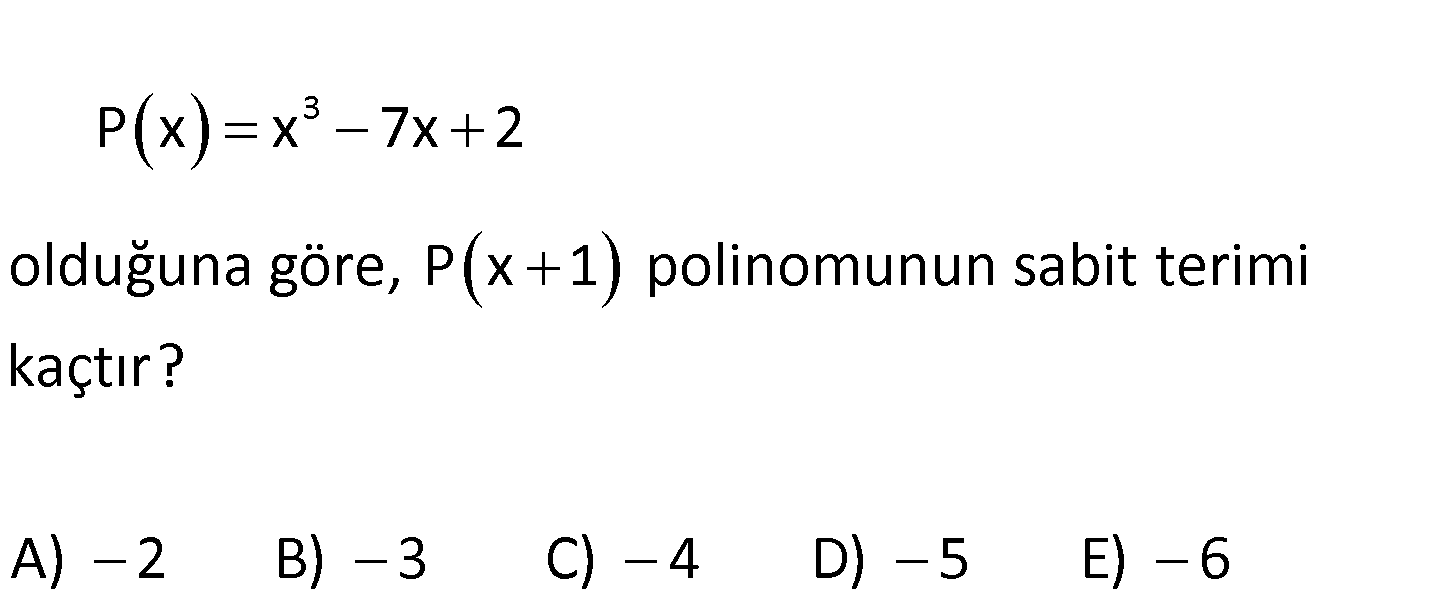

4.SORU


5.SORU


6.SORU
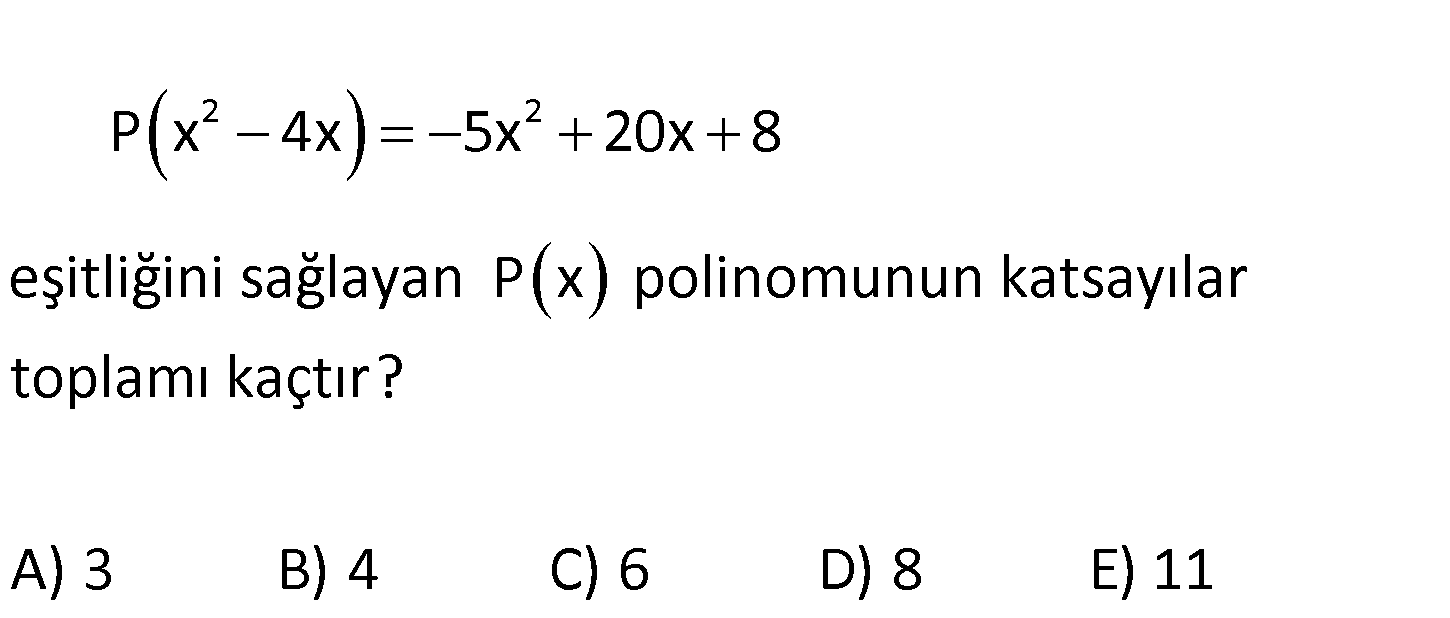

7.SORU

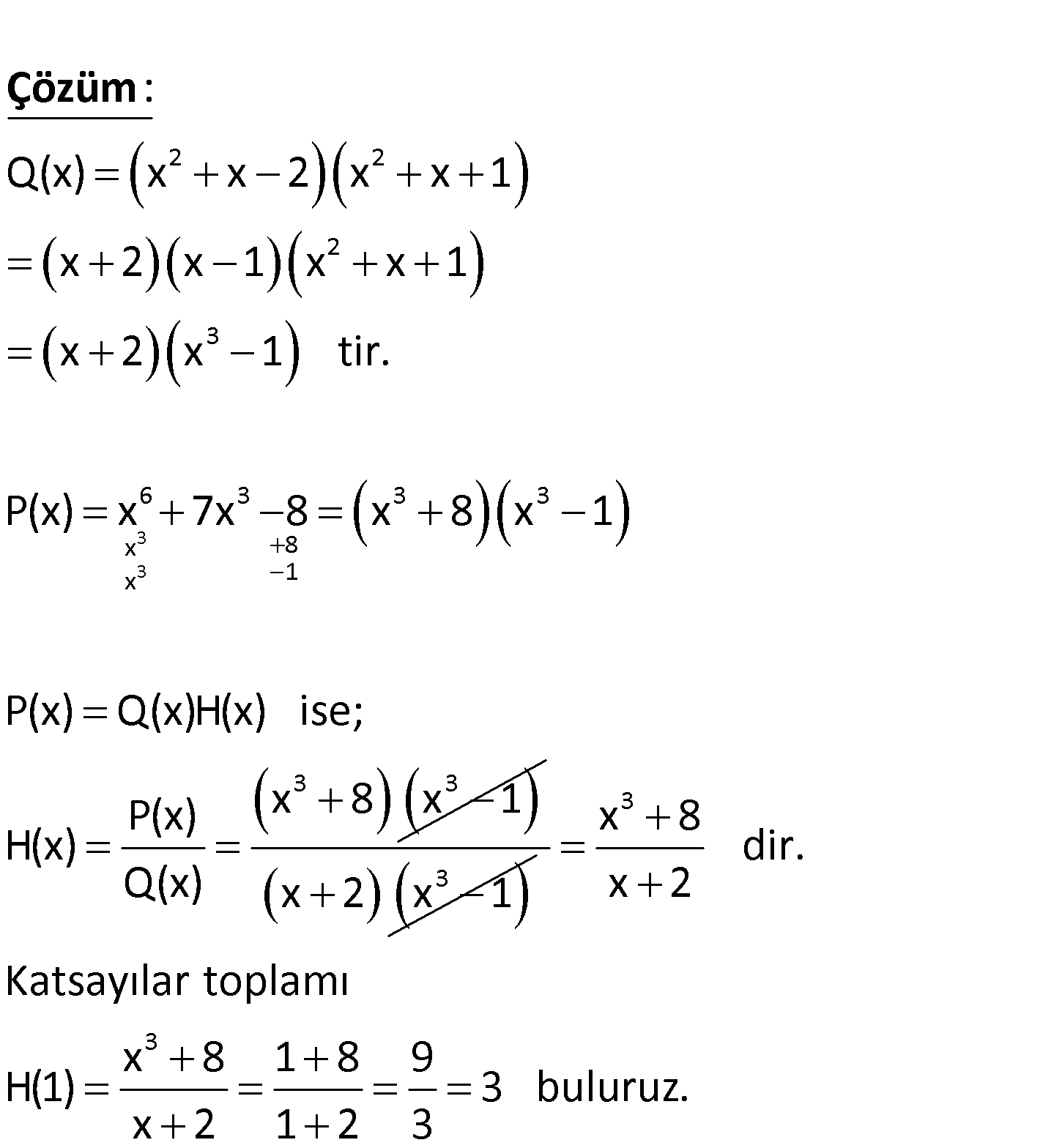
8.SORU


9.SORU

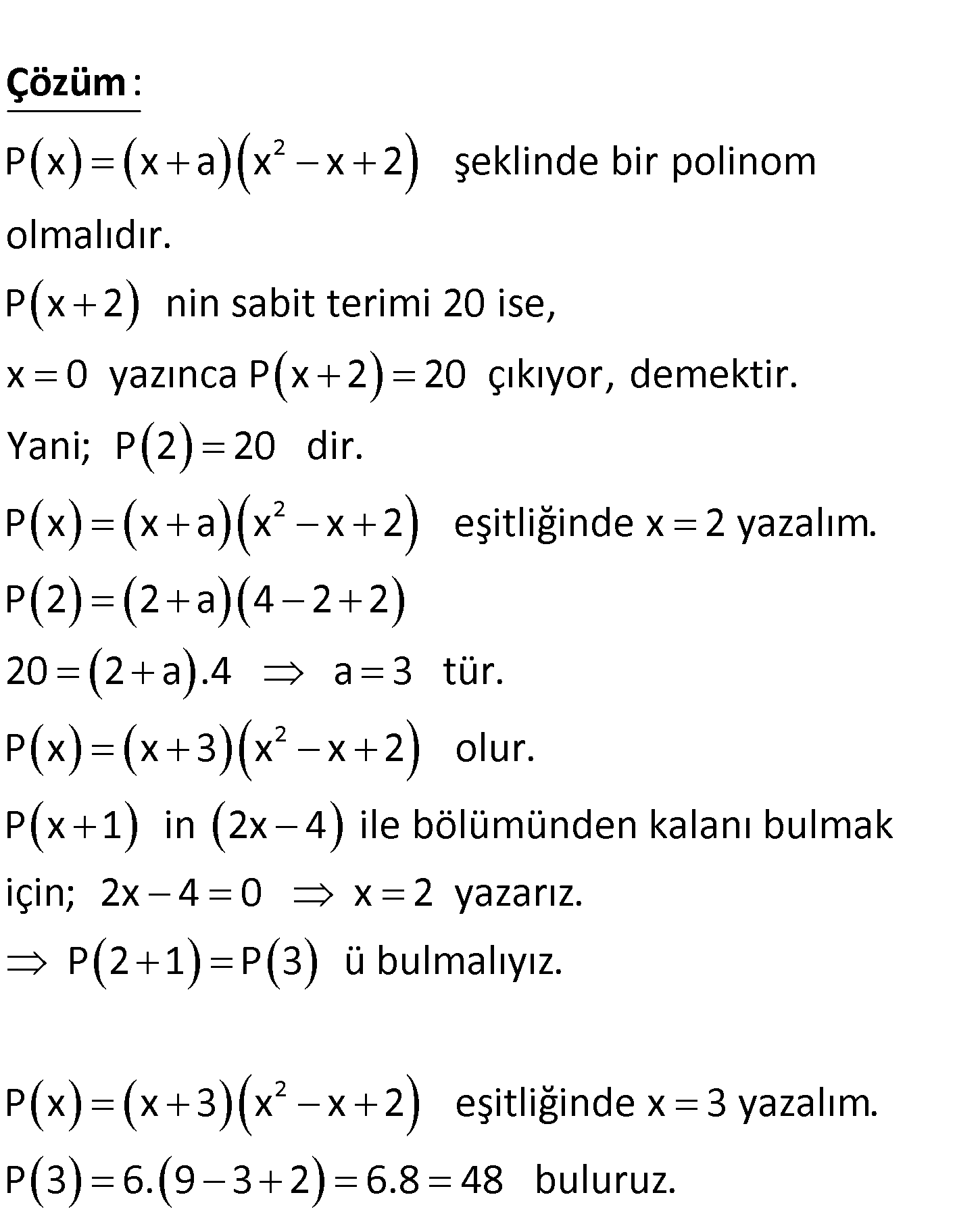
10.SORU
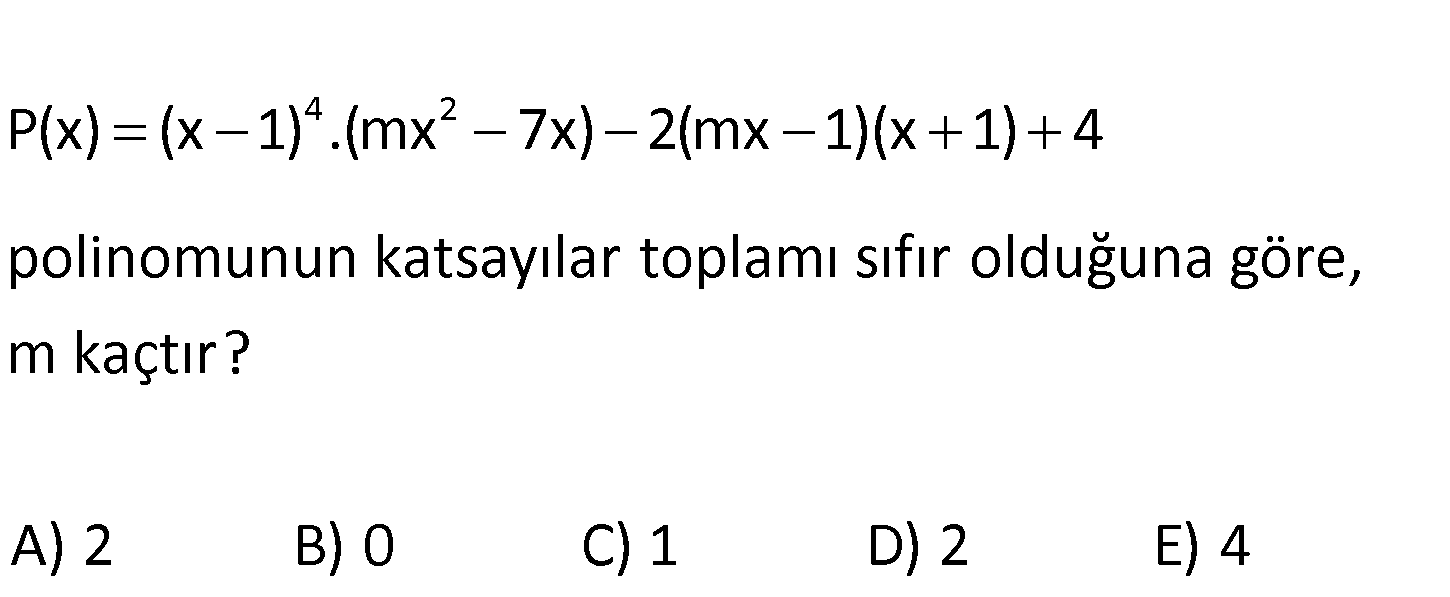

11.SORU

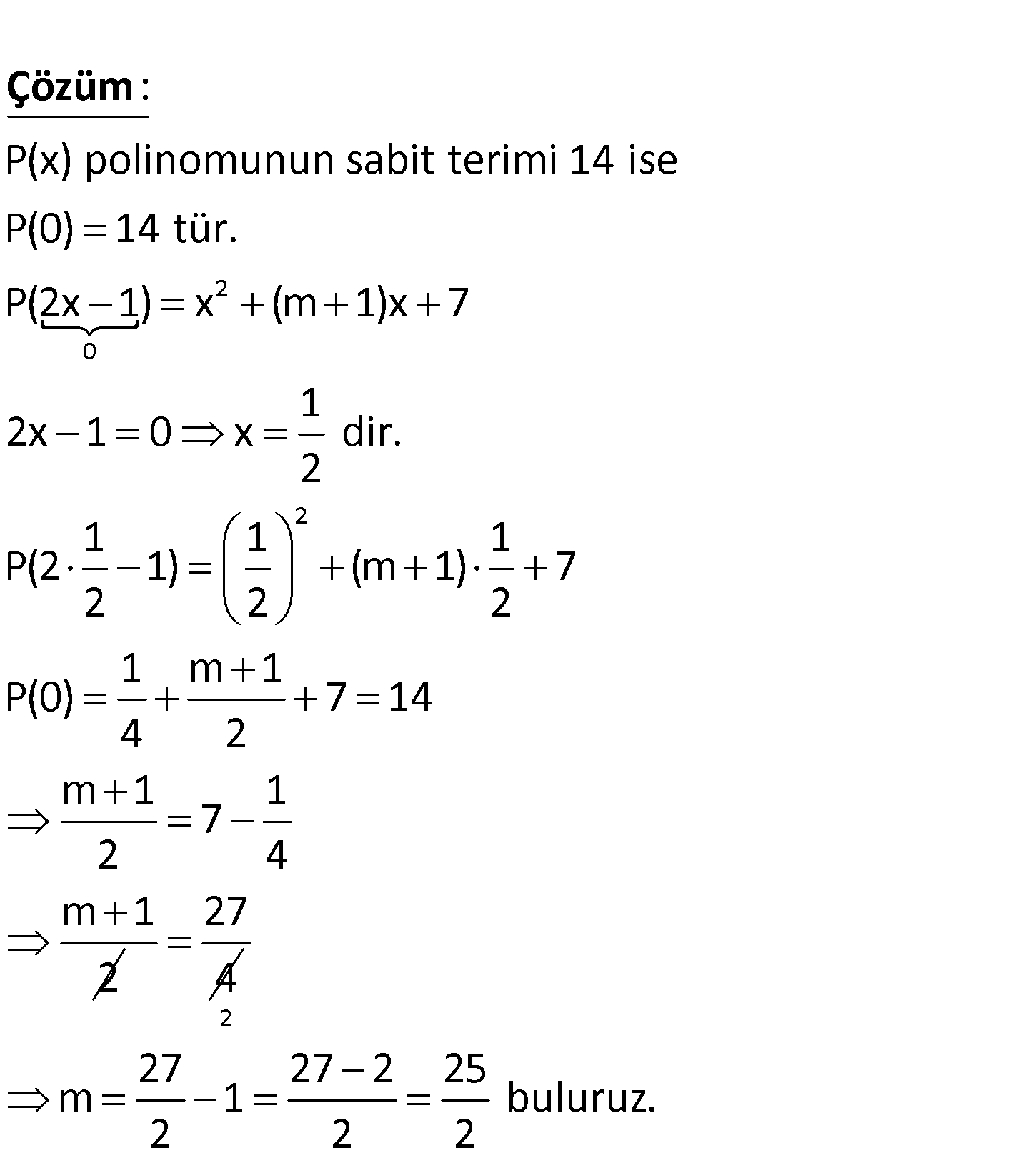
12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 3 2 P x 3 3x 4x k 1 polinomunun katsayılar toplamı 5 olduğuna göre, P 2x 1 polinomunun katsayıla r toplamı kaçtır? A) 14 B) 52 C) 96 D) 120 E) 134 3 2 3 P(x 3) 3x 4x k 1 katsayılar toplamı için x 1 yazılır. 3 4 k 1 5 ise, k 5 t : ir. P(x 3) 3x 4 Çözüm 2 3 2 3 2 3 2 4 x 5 1 P(x 3) 3x 4x 6 dır. P(2x 1)’in katsayılar toplamı için x 1 yazılır. P(2 1) P(1) i bulmalıyız. Aşağıdaki polinomda x 4 yazarsak, P(1) i bulabiliriz. P(x 3) 3x 4x 6 3.4 4.4 6 3.64 4.16 6 192 64 6 128 6 134 buluruz. 23
2 3 2 P x 3 x 2x m . x m P 2x 1 in katsayılar toplamı 243 olduğuna göre, m kaçtır? www.matematikkolay.net Katsayılar toplamını bulmak için x 1 yazılır. P 2x 1 in katsayılar toplamı 243 ise P 2. : 1 1 2 Çözüm 2 3 2 2 3 2 3 2 5 5 43 P 3 243 tür. P x 3 x 2x m x m eşitliğinde x yerine 0 yazarsak; P 0 3 0 0 m 0 m P 3 m .m 243 m 243 m m 3 buluruz. 80
3 P x x 7x 2 olduğuna göre, P x 1 polinomunun sabit terimi kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 3 P(x 1) polinomunun sabit terimi için x 0 yazılır. P(0 1) P(1) değerini bulalım. P(x) x x P( : 7 2 Çözüm 3 1) 1 7.1 2 P(1) 1 7 2 4 buluruz. www.matematikkolay.net 109
m 3 3 P x x 4x 5x m 3 polinomunun sabit terimi 4 olduğuna göre, dere – cesi kaçtır? www.matematikkolay.net m 3 3 sabit terim P(x) x 4x 5x m 3 m 3 4 m 7 m 7 dir. Şimdi m değerini yerine yazalım. P(x : ) Çözüm 7 3 3 4 3 x 4x 5x 7 3 P(x) x 4x 5x 4 derP(x) 4 buluruz. 103
www.matematikkolay.net n 1 2 n Katsayıları birbirinden farklı pozitif tam sayılar olan P x a .x a .x … a x polinomunun Katsayılar toplamı 2A A Katsayılarının aritmetik ortalaması 2 olduğuna göre, P 2 nin alabileceği en küçük değer kaçtır? A) 12 B) 24 C) 36 D) 48 E) 52 1 2 3 4 n 1 2 3 4 n Katsayılar toplamı a a a a … a 2A A Ortalaması ise, 2 a a a a … a : A n 2 2A Çözüm A n 2 3 4 1 2 3 4 4 3 2 1 2 n 2.2 4 tür. 2 Demek ki; P(x) a x a x a x a x tür. Katsayılar birbirinden farklı pozitif tam sayı ise, a 1, a 2, a 3 , a 4 seçelim ki en küçük değeri elde edelim. P(x) 4x 3x 2 3 4 2 3 4 x x olur. P(2) 4.2 3.2 2.2 2 8 12 16 16 52 buluruz. www.matematikkolay.net 69
2 2 P x 4x 5x 20x 8 eşitliğini sağlayan P x polinomunun katsayılar toplamı kaçtır? A) 3 B) 4 C) 6 D ) 8 E) 11 www.matematikkolay.net 2 2 2 2 k k P(x 4x) 5x 20x 8 P(x 4x) 5 x 4x 8 P(k) 5k 8 dir. O halde; P(x) 5x 8 ya : zabi Çözüm liriz. Katsayılar toplamı için x 1 yazalım. P(1) 5 8 3 buluruz. 60
6 3 2 2 P x x 7x 8 Q x x x 2 x x 1 polinomları veriliyor. P x Q x .H x olduğuna göre, H x polinomunun katsayılar top – lamı kaçtır? A) 9 B) 6 C) 3 D) 2 E) 1 3 3 2 2 2 3 6 3 3 3 x 8 x 1 Q(x) x x 2 x x 1 x 2 x 1 x x 1 x 2 x 1 tir. P(x) x 7x 8 : x 8 x 1 P(x) Q(x)H(x) i Çözüm 3 3 se; P(x) x 8 x 1 H(x) Q(x) 3 x 2 x 1 3 3 x 8 dir. x 2 Katsayılar toplamı x 8 1 8 9 H(1) 3 buluruz. x 2 1 2 3 www.matematikkolay.net 43
2 P x polinomunun sabit terimi 2 ve Q x 2 4x 2x 8 P x 2 olduğuna göre Q x 3 polinomunun katsayılar toplam ı kaçtır? A) 10 B) 20 C) 30 D) 40 E) 50 www.matematikkolay.net Sabit terimi 2 ise P(0) 2 dir. Q(x 3)’ün katsayılar toplamı x 1 verilerek bulunur. x 1 içi : n Çözüm 2 2 Q(1 3) Q(4)’ü bulmalıyız. Buna göre; Q(x 2) 4x 2x 8 eşitliğinde x 2 yazarsak P(x 2) Q(4)’ü bulabiliriz. Q(2 2) 4.2 2.2 8 P(2 2) Q(4) 16 4 P(0) Q(4) 8 20 2 Q(4) 40 buluruz. 9
2 Başkatsayısı 1 olan üçüncü dereceden P x polino – mu x x 2 ile tam bölünebilmektedir. P x 2 polinomunu n sabit terimi 20 olduğuna göre, P x 1 polinomunun 2x 4 ile bölümünden elde edilen kalan kaçtır? A) 48 B) 40 C) 36 D) 32 E) 24 www.matematikkolay.net 2 P x x a x x 2 şeklinde bir polinom olmalıdır. P x 2 nin sabit terimi 20 ise, x 0 yazı ca : n P Çözüm 2 2 x 2 20 çıkıyor, demektir. Yani; P 2 20 dir. P x x a x x 2 eşitliğinde x 2 yazalım. P 2 2 a 4 2 2 20 2 a .4 a 3 tür. P x x 3 x x 2 olur. P x 1 in 2x 4 ile bölümünden kalanı bulmak için; 2x 4 0 x 2 2 yazarız. P 2 1 P 3 ü bulmalıyız. P x x 3 x x 2 eşitliğinde x 3 yazalım. P 3 6. 9 3 2 6.8 48 buluruz. 86
4 2 P(x) (x 1) .(mx 7x) 2(mx 1)(x 1) 4 polinomunun katsayılar toplamı sıfır olduğuna göre, m kaçtır? A) 2 B) 0 C) 1 D) 2 E) 4 www.matematikkolay.net 4 2 4 Polinomun katsayılar toplamı 0 ise; P(1) 0 dır. P(x) (x 1) .(mx 7x) 2(mx 1)(x 1) 4 P(1) ( 1 : 1 ) Çözüm 2 0 2 .(m.1 7.1) 2(m.1 1)(1 1) 4 0 4(m 1) 4 4 m 1 1 4 m 1 1 m 2 buluruz. 111
2 P(2x 1) x m 1 x 7 polinomu veriliyor. P x in sabit terimi 14 olduğuna göre, m kaçtır? 25 A) 7 B) 8 C) D 2 27 ) E) 14 2 www.matematikkolay.net 2 0 P(x) polinomunun sabit terimi 14 ise P(0) 14 tür. P(2x 1) x (m 1)x 7 1 2x 1 0 x dir. 2 1 P(2 1 2 : Çözüm 2 1 1 ) (m 1) 7 2 2 1 m 1 P(0) 7 14 4 2 m 1 1 7 2 4 m 1 2 27 4 2 27 27 2 25 m 1 buluruz. 2 2 2 112
P x polinomunun katsayılar toplamı 3, Q x 1 P x 1 olduğuna göre, Q x polinomunun sabit terim i kaçtır? A) 4 B) 3 C) 2 D) 1 E) 1 P(x) polinomunun katsayılar toplamı P(1) 3 Q(x) polinomunun sabit terimi Q(0) dır. Q(x 1 x) : ) P( Çözüm 1 x 1 yazalım. Q(1 1) P(1) 1 Q(0) P(1) 1 Q(0) 3 1 2 buluruz. 127


Nerden soru sorabilirim acaba.
Bir kac tane var da.
Soru almıyoruz şu an.
Peki soru sorabiliyo muyuz
Soru almıyoruz