Soru Sor sayfası kullanılarak Polinomlar konusu altında Kaç tanesi polinomdur, Polinom olabilme, polinom belirtmesi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU
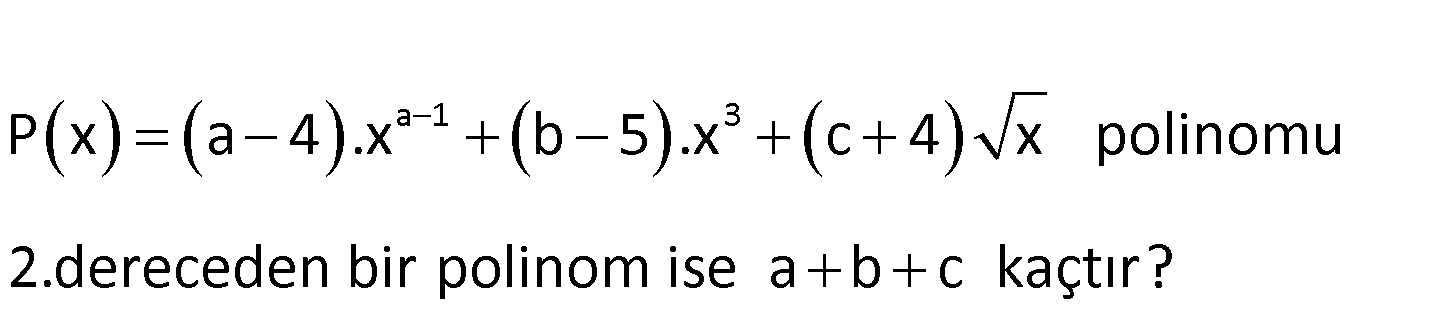

4.SORU
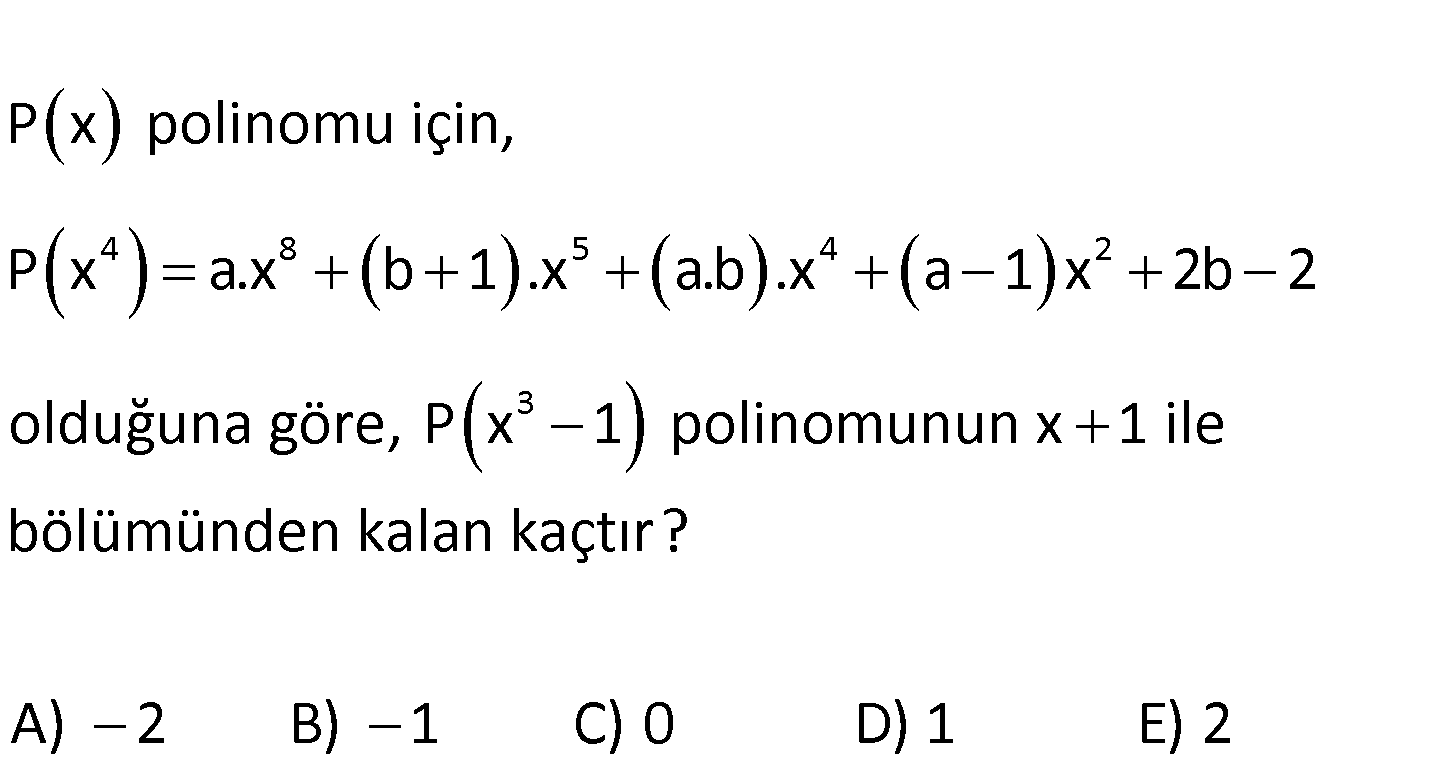

5.SORU


6.SORU


7.SORU


8.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
5 3 2 4 3 5 3 I. P x x x 4 5x 1 II. Q x x x 7 x x 1 III. R x x IV. T x x x 4 5x 1 V. B x 8 Yukarıda verilen ifa delerden kaç tanesi polinomdur? A) 1 B) 2 C) 3 D) 4 E) 5 1 x’in derecesi doğal sayı olmalıdır. 1 III. öncül x sebebiyle polinom olamaz. x IV.öncü : l x Çözüm 1 x2 sebebiyle polinom olamaz. Diğer 3 öncülde polinom olmalarını engelleyecek bir durum olmadığından cevap 3 tür. 2
18 n n n 2 n 7 P(x) 3x 5x 4x 7n ifadesi bir polinom belirttiğine göre n’nin alabileceği değerler to plamı kaçtır? A) 39 B) 38 C) 30 D) 28 E) 27 www.matematikkolay.net 18 n n n 2 n 7 P(x) 3x 5x 4x 7n x’in dereceleri doğal sayı olmalıdır. n 2 0 n 2 dir. n 7 0 : Çözüm n 7 dir. 18 n 18 18 0 1 0 1 olmalıdır. n n n 2 ve 2’den büyük 18’i bölen n sayıları; 2,3,6,9,18 toplamları 38 buluruz. 3
a 1 3 P x a 4 .x b 5 .x c 4 x polinomu 2.dereceden bir polinom ise a b c kaçtır? www.matematikkolay.net 2 a 1 3 0 0 polinom 2. dereceden polinom ise P(x) (a 4)x (b 5)x (c 4) x a 1 2 a 3 olur. b 5 0 b o : 5 Çözüm lur. c 4 0 c 4 olur. a b c 3 5 4 4 bulunur. 12
www.matematikkolay.net 4 8 5 4 2 3 P x polinomu için, P x a.x b 1 .x a.b .x a 1 x 2b 2 olduğuna göre, P x 1 polinomunun x 1 ile bölümün den kalan kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 4 8 5 4 2 4 P x ax b 1 x ab x a 1 x 2b 2 polinomu x e göre verilmiş. Biz bunu x ‘e göre yazmak isterse : k Çözüm 4 5 1 2 4 2 0 olmalı 0 olmalı , x ün üssünü 4’e bölmemiz gerekir. Karşı tarafta da aynı işlemi yapacağız. Yani; P x ax b 1 x ab x a 1 x 2b 2 olur. Polinomda x’lerin üssü doğal sayı şeklinde olmalıydı. Bu s 2 3 3 2 ebeple; b 1 ve a 1 olmalıdır. P x x x 4 olur. P x 1 in x 1 ile bölümünden kalanı bulmak için x 1 yazarız. P 1 1 P 2 yi bulmalıyız. P 2 2 2 4 4 2 4 2 buluruz. 84
www.matematikkolay.net 15 n P x 2.x 3x 4 ifadesini polinom yapan n değerlerini bulunuz. 15 n P(x) 2x 3x 4 ifadesinin polinom olabilmesi için; 15 ifadesinin bir doğal sayı olması ger : e n Çözüm kir. n, 15’i tam bölen doğal sayılar olmalı n {1,3,5,15} buluruz. 123
www.matematikkolay.net 9 n n 4 P x 5x 4x ifadesini polinom yapan n sayılarının en büyüğü ile en küçüğünün toplamı kaçtı r? 9 n n 4 P(x) 5x 4x polinom olması için x ‘in kuvveti en az sıfır olmalı. 9 n 0 : 9 n n 4 0 n 4 n Çözüm ‘nin en küçük değeri 4, en büyük değerini 9 dur. Toplamları da 9 4 5 buluruz. 143
18 n n 3 P x x x 4 polinom ise n’nin alabileceği değerler nedir? 18 n n 3 P(x) x x 4 polinomlarda üsler doğal sayı olmalıdır. n n, 3’ün katı olmalıdır. 3,6,9 : 3 Çözüm ,12,15,18,… 18 n, 18’i bölmelidir. yukarıdakilerden n 3,6,9,18 değerleri olabilir. Cevap: n’in alabileceği değerler 3,6,9,18 www.matematikkolay.net 147
2 6 4 3 2 P x 3x 5x a 2 x 5x 3a olmak üzere P x polinomunun sabit terimi kaçtır? A) 12 B) 6 C) 4 D)2 E) 6 www.matematikkolay.net 2 2 6 4 3 0 P(x ) polinomunda tüm terimler çift dereceli olmak zorunda.Buna göre; P(x ) 3x 5x (a 2 x 5 : ) Çözüm 2 2 6 4 2 3 2 x 3a a 2 0 a 2 dir. P(x ) 3x 5x 5x 6 P(x) 3x 5x 5x 6 P(x) polinomunun sabit terimi 6 bulunur.


Sayfayı çok beğendim soruların altında çözümlerin olması çok hoşuma gitti