Soru Sor sayfası kullanılarak Permütasyon konusu altında Şekilli Kaç farklı yol vardır soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

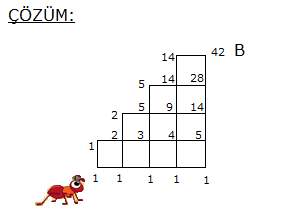

3.SORU



4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
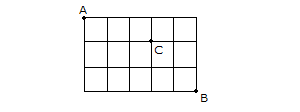
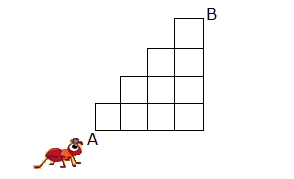
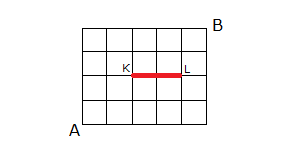
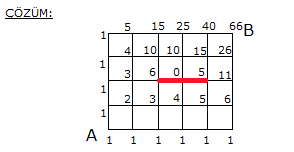
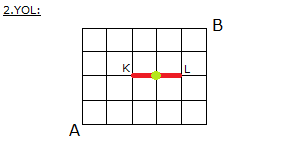
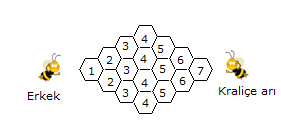
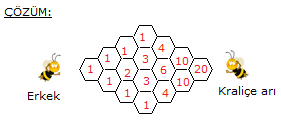
A’dan hareket eden bir kimse, C ye uğrayarak B noktasına en kısa yoldan gitmek istemektedir. Buna göre, bu kişi A dan B ye kaç farklı şekilde gidebilir? A) 36 B) 30 C) 24 D) 18 E) 12 www.matematikkolay.net Çözüm: A’dan C’ye ulaşmak için 1 kere Aşağıya, 3 ker e Sağa gidilmelidir. 4! ASSS Tekrarlı permütasyon 4 farklı yol 3! C’dan B’ye ulaşmak için 2 kere Aşağıya, 2 ker e Sağa gidilmelidir. AASS Tekrarlı permüta 4! syon 6 farklı yol 2!.2! Tüm yol için ise 4.6 24 farklı seçenek vardır. 12 Telden yapılmış ve birbirine özdeş 10 adet kareden oluşan şekildeki yapının A noktasında bulunan bir karınca, yalnız biçiminde yönleri kullanarak en kısa yoldan B noktasına gitmek istiyor. Buna göre, A dan B ye kaç farklı biçimde gidebilir. A) 38 B) 42 C) 47 D) 52 E) 63 www.matematikkolay.net Her köşe noktasına farklı ulaşım sayısı, kendisinden önceki köşelere ulaşım sayısının toplamı kadardır. Yani solundaki ve altındaki noktaları toplayarak ilerleyeceğiz. Şekilde A noktasından 1 yazarak başlarsak, B noktası – na 42 farklı şekilde ulaşıldığını bulabiliriz. 25 www.matematikkolay.net Yukarıdaki şekilde, A şehri ile B şehri arasındaki yollar birim kareler ile gösterilmiştir. K ile L noktaları arasında yol çalışması yapıldığı için kullanılamamaktadır. Buna göre, A şehrinden B şehrine gitmek isteyen bir araç en kısa yoldan kaç farklı şekilde gidebilir? A) 48 B) 54 C) 60 D) 66 E) 72 Her köşe noktasına farklı ulaşım sayısı, kendisinden önceki köşelere ulaşım sayısının toplamı kadardır. Yani solundaki ve altındaki noktaları toplayarak ilerleyeceğiz. Şekilde A noktasından 1 yazarak başlarsak, B noktası – na 66 farklı şekilde ulaşıldığını bulabiliriz. (KL’nin orta noktasını kullanamayız. 0 yazdık. ) www.matematikkolay.net Normalde KL yolunde çalışma olmasaydı; A’dan B’ye gitmek için 5 kere sağ, 4 kere yukarı yön – de gidilecekti. SSSSSYYYY Tekrarlı permütasyonla hesaplayabiliriz. 9! 9.8.7.6. 5! 4!5! 4!. 5! 9 3 . 8 .7.6 04.03.2002 3.7.6 126 dır. .1 Ancak, KL’nin orta noktasını kullanamıyoruz. Bu nokta kullanılarak gidilen farklı yol sayısını çıka – rarak cevabı bulabiliriz. A’dan , KL’nin orta noktasına kadar; 5! SSSYY 10 f 3!2! arklı yol KL’nin orta noktasından B’ ye kadar; 4! SSYY 6 farklı yol var. 2!2! A’dan B’ye bu nokta kullanılarak 10.6 60 farklı şekilde gidilebilir. Tümden çıkaralım 126 60 66 buluruz. 26 www.matematikkolay.net 1 numaralı petekteki erkek arı, 7 numaralı petekteki kraliçe arıya, peteklerin üzerinden komşu petekleri takip ederek aynı numaralı peteği birden fazla kullanmamak kaydıyla kaç farklı şekilde ulaşılabilir? A) 36 B) 20 C) 28 D) 35 E) 15 1 numaralı petekten itibaren her peteğe kaç farklı yoldan gelinebileceğini peteklerin üzerine yazalım. Her peteğe onun solunda kalan ve onunla farklı numaralı olan peteklerin üzerindeki ulaşım yolu sayıları toplamı kadar ulaşma yolu var dır. Örneğin 2 numaralı peteklere ulaşma yolu 1 tanedir. Bundan sonraki ortadaki 3 numaralı peteğe ulaşma yolu 2 numaralı peteklere ulaşma yollarının toplamıdır. Aynı şekilde devam edilirse 7 numaralı peteğe; 6 numaralı peteklere ulaşma yollarını toplamı; Yani ; 10 10 20 farklı yolla ulaşılır. www.matematikkolay.net 27

