Soru Sor sayfası kullanılarak Olasılık konusu altında Şekilli Olasılık ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU

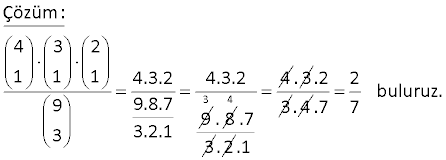
6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
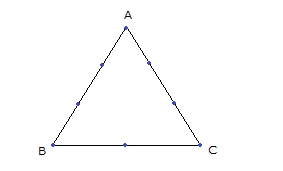
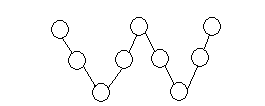
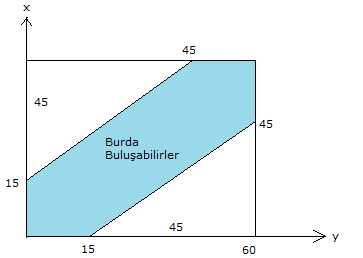
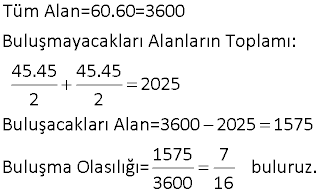
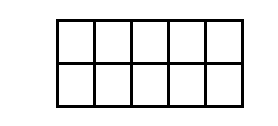
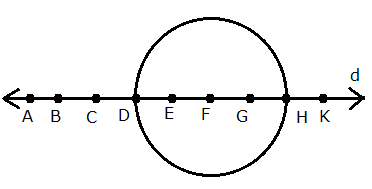
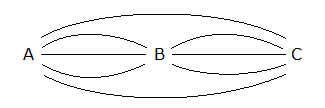
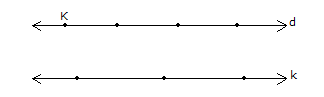
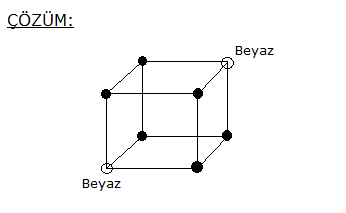
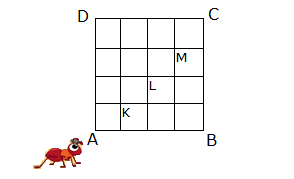
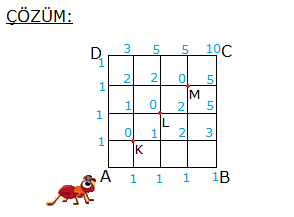
Yukarıdaki üçgen üzerinde 8 nokta veriliyor. Köşeleri bu noktalardan üçü olan üçgenler arasından seçilen bir üçgenin bir kenarının [AB] üzerinde olma olasılığı kaçtır ? 16 18 20 24 2 A) B) C) D) E) 47 47 47 47 5 47 www.matematikkolay.net Çözüm: Bir üçgen için 3 nokta seçilir; ama doğrusal olan noktalardan 3 nokta seçerek üçgen çizilemez. Buna göre çizilebilecek üçgen sayısı; 8 4 4 3 56 4 4 1 47 dir. 3 3 3 3 [AB] kenar lı üçgenler için [AB] üzerinden iki nokta seçilmeli, diğer nokta ise kalan noktalardan biri olmalı. Buna göre; 4 4 6.4 24 üçgen olur. 2 1 24 Olasılık buluruz. 47 7 Üzerinde 9 tane lamba bulunan şekildeki ışıklı uyarı levhasında anahtar kapandığında rastgele iki lamba yanmaktadır. Buna göre, art arda gelen iki lambanın yanma olası – lığı kaçtır? 5 1 2 A) B) C) D) 36 9 9 1 5 E) 3 9 www.matematikkolay.net Çözüm: En uçta 2 lamba, içerde ise 7 lamba vardır. En uçtaki lambalardan biri yandığında, istenen koşulu; kalan 8 lambadan tek bir lamba yanarak sağlayabilir. 2 1 1 9 8 36 İçerdeki lambalardan biri yandığında , istenen koşulu; kalan 8 lambadan 2 lamba yanarak sağlayabilir. 7 2 7 9 8 36 1 7 8 2 Toplam buluruz. 36 36 36 9 13 Ecem ile Ceren 16.00 ile 17.00 arasında buluşacak lardırHer gelen sadece 15 dakika bekleyecek ve 15 dakika içerisinde diğeri gelmez ise buluşmadan gidecektir. Ecem ile Ceren in buluşma olasılığı? Çözüm: 16: 00 ile 17:00 arasında 60 dk var. Ecem’in geldiği zamana x diyelim; 0,……x,……60 Ceren’in geldiği zamana y diyelim; 0,……y,……60 Buluşma’nın gerçekleşmesi için x ile y’nin arasındaki fark, 15 dk’dan küçük olmalıdır. Yani; |x y| 15 olmalıdır. Bu soruyu geometrik olarak ele alalım ve olasılığı bulalım. www.matematikkolay.net Tüm Alan=60.60=3600 Buluşmayacakları Alanların Toplamı: 45.45 45.45 2025 2 2 Buluşacakları Alan=3600 2025 1575 1575 7 Buluşma Olasılığı= buluruz. 3600 16 30 Birbirine eş 10 küçük karenin biraraya gelmesiyle oluşan dikdörtgen şekildeki gibidir. Buna göre, rastgele seçişen bir dikdörtgenin bu 10 eş kareden biri olma olasılığı kaçtır? 2 2 2 1 A) B) C) D) E) 9 7 5 2 1 3 www.matematikkolay.net Çözüm: Şekilde kaç tane dikdörtgen var bulalım. Bir dikdörtgeni oluşturmak için 2 yatay çizgi ve 2 dikey çizgiye ihtiyacımız var dır. 6 6 dikey çizgiden 2’si seçilecek 2 3 yatay çizgiden 2’si deçile 3 cek 2 6 3 Buna göre dikdörgen sayısı 15.3 45 tir. 2 2 10 2 Olasılık da buluruz. 45 9 32 Şekildeki d doğrusu üzerinde 9 nokta verilmiştir. Seçilecek üç noktadan birinin çemberin dışında, birinin çemberin üzerinde, birinin çemberin iç bölgesinde olma olasılığı kaçtır? 4 3 4 A) B) C) D) 5 5 7 3 2 E) 7 7 www.matematikkolay.net Çözüm: 4 3 2 1 1 1 4.3.2 4.3.2 9 9.8.7 9 3 3.2.1 3 . 8 4 .7 03.Şub 4 .1 . 3.2 03.Nis 2 buluruz. .7 7 40 A ve B şehirleri arasında 3 yol, B ve C şehirleri ara – sında 4 yol ve A dan C ye direkt 2 yol vardır. Buna göre, A dan C ye giden bir aracın B ye uğrayıp C ye gitmiş olma olasılığı kaçtır? 2 2 A) B) 9 3 7 6 C) D) E) 7 7 9 7 www.matematikkolay.net Çözüm: B’ye uğrayarak A ‘dan C’ ye 3.4 12 farklı yoldan gidi – lebilir. A’dan C’ye de 2 farklı yol var dır. Yani toplamda 14 farklı yol var dır. 12 12 Buna göre olasılık 14 6 14 7 6 buluruz. 7 43 Şekildeki gibi 3 satır, 3 sütun halinde 9 eş bölmeden oluşan bir kutuya 3 top her bölmeye en çok bir top gelmek şartıyla konuyor. Buna göre, sadece 2 topun aynı satırda olma olasılığı kaçtır? 1 A) B) 7 3 5 1 9 C) D) E) 14 14 2 14 www.matematikkolay.net Çözüm: 1. topu istediğimiz yere koyalım. 2 2. topu bununla aynı satıra koyma olaslığımız dir. 8 6 3. topu aynı satıra koymama olasılığı ise dir. 7 2 6 12 8 7 56 Veya; 1.topu gene rastgele bir y ere koyalım. 6 2. topu bununla aynı satıra koymama olasılığı dir. 8 3. topu da bunlardan biri ile aynı satıra koyma 4 6 4 24 olasılığı dir. 7 8 7 56 12 24 36 9 Olasılıkları toplayalım. buluruz. 56 56 56 14 47 Şekilde d / /k dır. Verilen 7 noktayı köşe kabul eden üçgenler çiziliyor. Çizilen üçgenlerin içerisinden rasgele seçilen bir üçgenin köşelerinden birinin K olma olasılığı kaçtır ? 1 1 2 2 A) B) C) D) 4 3 3 3 E) 5 5 Çözüm: Üçgen çizebilmek için, d doğrusundan 2 nokta, k noktasından 1 nokta 4 3 seçebiliriz. 6.3 18 2 1 veya d doğrusundan 1 nokta, k noktasından 2 4 3 nokta seçebiliriz. 4.3 12 1 2 dir. Toplam 30 tane üçgen çizilebilir. 3 3 Bir köşesi K ise; d’den 1 k ‘dan 1 nokta 9 1 1 3 veya k’dan 2 nokta 3 2 Bir köşesi K olan toplam 3 9 12 üçgen var dır. 12 Olasılık 2 30 5 2 buluruz. 5 www.matematikkolay.net 58 Bir küpün 8 köşesinden 6’sı siyaha, diğer 2’si beyaza rastgele boyanıyor. Bu küpte, iki ucu da beyaza boyalı olan bir ayrıt bulunmama olasılığı kaçtır ? 4 1 3 2 6 A) B) C) D) E) 7 7 7 7 7 www.matematikkolay.net Bir köşeyi beyaza boyayalım. Küpün bundan hariç 7 farklı köşesi var dır. Bu köşeyle komşu olmayan sadece 1 noktası var dır. Diğer 6 köşenin komşusu var dır. Bir ayrıtın iki ucunun da beyaz olmamasını istiyorsak Komşu olmayan köşeyi beyaza boyamak gerekiyor. 1 Bu sebeple olasılık buluruz. 7 64 Yukarıdaki şekilde ABCD karesi 16 eş kareye bölünmüştür. A dan hareket eden bir karınca sağa veya yukarı doğru hareket ederek C noktasına gidecektir. Karıncanın K, L, M noktalarının en az birinden geçme olasılığı kaçtır? 1 2 3 4 6 A) B) C) D) E) 5 5 5 5 7 www.matematikkolay.net KLM noktalarına uğramadan 10 farklı yoldan gidebilir. Tüm durum ise; 8! 8 SSSSYYYY 4!.4! 2 .7. 6 .5 4 . 3.2.1 70 tir. KLM’den hiçbirine uğramadan gitme olasılığı 10 1 dir. 70 7 1 6 En az birinden geçme olasılığı 1 buluruz. 7 7 70


süper sorular