Soru Sor sayfası kullanılarak Olasılık konusu altında Birarada olup olmama olasılıkları, ekip soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU

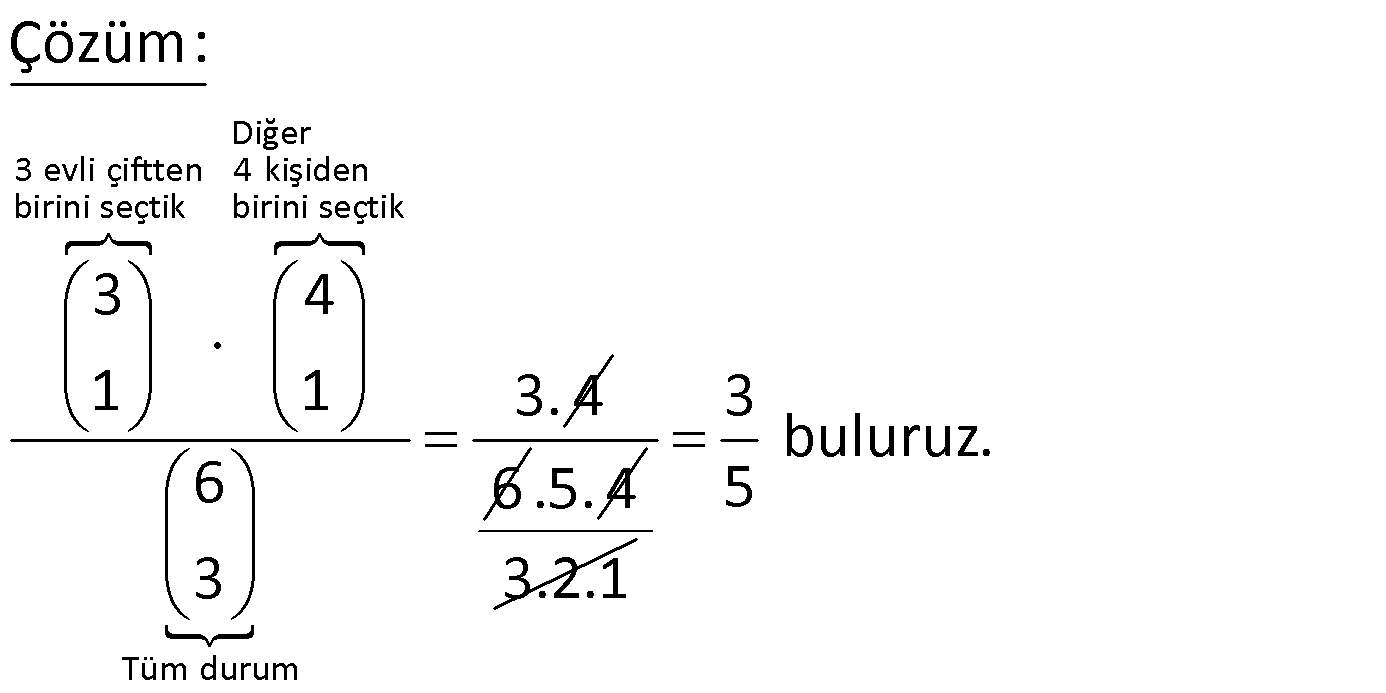
6.SORU


7.SORU

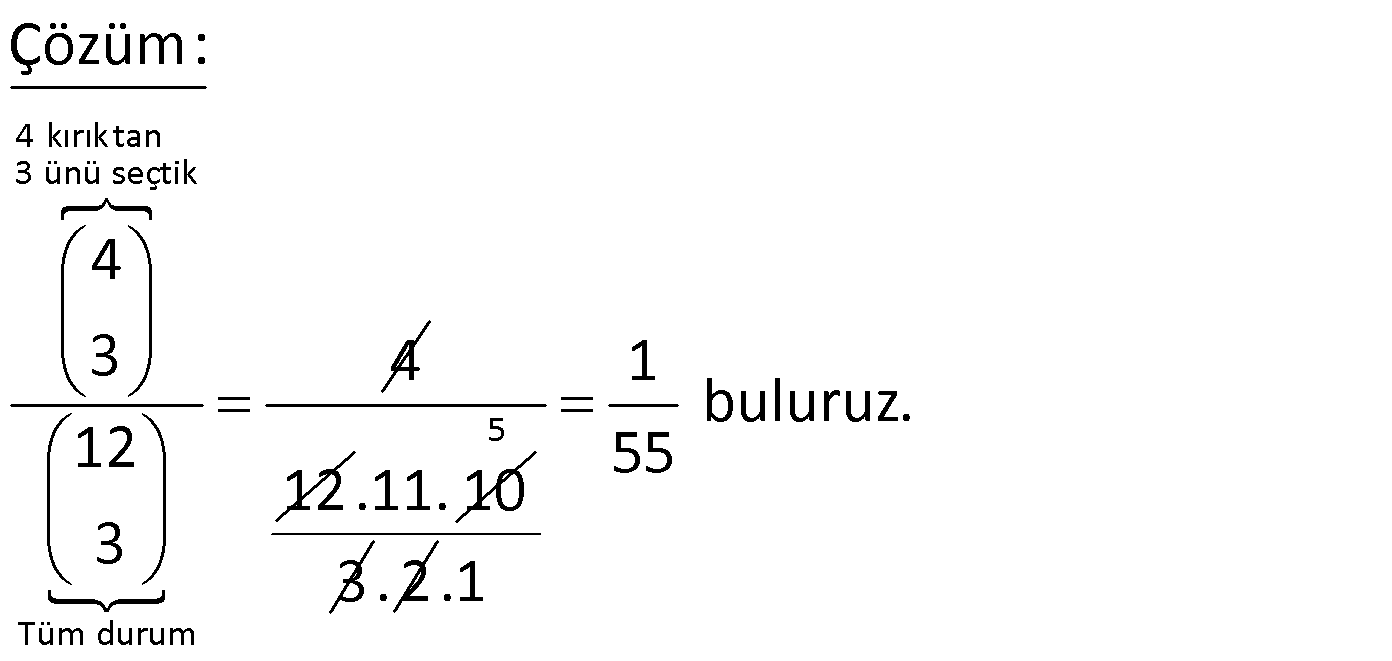
8.SORU


9.SORU


Diğer Soru Tipleri için Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
3 kız, 4 erkek öğrenci yan yana oturuyor. Buna göre, erkek öğrencilerin bir arada olmama olasılığı kaçtır? 3 26 4 6 31 A) B) C) D) E) 7 35 5 7 35 Çözüm: Tüm durumlar 7! dir. Erkeklerin bir arada olma durumu: Erkekleri 1 kişi kabul ederek yapalım. Sonra erkekle – ri kendi arasında sıralayalım. (3 kız erkekler).(Erkekler kendi arasında) 4!.4! duru m vardır. Erkeklerin bir arada olmama durumu ise; 7! 4!.4! durum vardır. 7! 4!.4! 4! Olasılık 7! (7.6.5 4!) 7.6.5. 4! 210 24 31 buluruz. 210 35 2 A {Ali, Mehmet, Sezen, Meral} B {Adem, Mehmet, Meral, Cemil, Nur} kümeleri iki öğrenci grubunu temsil etmektedir. A ve B kümelerinden birer tane öğrenci alınarak iki kişilik ekipler oluş turuluyor. Buna göre, bu ekiplerden seçilen birinin aynı isimli öğrencilerden oluşma olasılığı kaçtır? 1 1 3 2 1 A) B) C) D) E) 10 9 10 5 2 www.matematikkolay.net Çözüm: Tüm ekip sayısı: 4 5 4.5 20 1 1 Aynı isimli durumar : (Mehmet,Mehmet) veya (Meral,Meral) olabilir. 2 durum 2 1 Olasılık buluruz. 20 10 10 Aralarında Seval ile Taner’in de bulunduğu 10 kişilik bir gruptan 4 kişi geziye gönderilecektir. Seval ile Taner’in birlikte geziye gitme olasılığı kaçtır ? 2 7 3 7 2 A) B) C) D) E) 15 20 10 30 3 Çözüm: 10 Tüm durumlar : 4 İstenen durum: Sevil ile Taner birlikte olsun, 8 kalan 8 kişiden de 2 kişi seçelim: 2 8 8.7 2 Olasılık 10 4 02.Oca 10.9. 8.7 4.3.2.1 1 10.Eyl 04.Mar 1 1 2 buluruz. 5.3 15 15 2.1 2 www.matematikkolay.net 17 4 kız ,4 erkek öğrencinin tamamı rastgele A veya B sınıfına yerleştirilecektir.Buna göre,her sınıfa ikişer kız öğrenci gitme olasılığı kaçtır? www.matematikkolay.net Çözüm: Erkeklerin dağılımı bizi ilgilendirmemektedir. Bu yüz – den hesaba katmayacağız. Her kız için 2 sınıf seçeneği var dır. Bu nedenle tüm durum 2.2.2.2 16 dır. 2’şerli gitmeleri için 4 kızdan 2’sini b ir sınıf için, 4 2 diğer ikisini diğer sınıf için seçeceğiz. 2 2 4 2 2 2 6.1 3 Olasılık buluruz. 16 16 8 31 3 evli çift arasından 3 kişi seçiliyor.Seçilen kişilerin arasında evli bir çiftin olma olasılığı kaçtır? Çözüm: Soruyu tersten düşünerek çözelim. İlk öncele rastgele birini seçelim. Geriye 5 kişi kalır. İkinci seçtiğimiz kişinin bunun eşi olmama olasılığı 4 tir. Geriye 4 kişi kalır. 5 Üçüncü seçtiğimiz kişinin de hem birincinin hem de 2 ikincinin eşi olmama olasılığı tür. 4 Buna göre bizden istenen olasılık; 4 1 2 5 4 2 3 1 buluruz. 5 5 www.matematikkolay.net 33 Aralarında Ali ve Veli nin de bulunduğu 10 kişiden 6 sı boş olan yan yana konulmuş 6 sandalyeye rastgele oturmuşlardır.Buna göre, sandalyelere oturanlar içinde hem Ali nin hem de Veli nin olması olasılığı kaçtır? Çözüm: Tüm durum: 10 kişiden 6 kişinin seçilerek rastgele oturması İstenen durum: Ali ve Veli’ yi yerleştirip, kalan 8 kişiden 4’ünün seçilerek rastgele oturması. İki durumda da 6 kişi olup, rastgele dizilim yapıla – cağı için nasıl dizildiklerini hesaplamaya gerek yok. Seçim sayısı arasındaki oran bize olasılığı verir. 8 8.7.6.5 4 4.3.2.1 Olasılık 10 6 10.9.8.7. 6.5 6.5. 4.3.2.1 08.Tem .6.5 10.9. 8.7 30 1 90 3 34 Bir kolideki 12 yumurtadan 4’ü kırıktır. Bu yumurtalardan rastgele seçilen 3 yumurtadan 3 ünün de kırık olma olasılığı kaçtır? 1 1 1 1 1 A) B) C) D) E) 12 22 36 42 55 www.matematikkolay.net Çözüm: 4 İlk yumurtanın kırık olma olasılığı= 12 Bir kırık yumurta azaldı. Toplam 11 yumurta var. 3 İkincinin kırık olma olasılığı= 11 2 Üçüncünün kırık olma olasılığı= dur. O halde; 10 4 Olasılık= 12 3 2 11 10 5 1 buluruz. 55 36 Ali, Burcu ve Can’ın aralarında bulunduğu altı kişi bir sinema salonunda yan yana rastgele oturacak – lardır. Burcu’nun Ali ve Can’a eşit uzaklıkta oturma olasılığı kaçtır? www.matematikkolay.net A ile C yer değiş 3 kişin 4 boşluk tan 3’ünü seçelim Çözüm: Ali Burcu ve Can’ın yan yana olduğu durumları he – sap edelim. ABC ve diğer 3 kişi 4!. 2! 48 durum Aralarında 1’er kişi olduğunda; 4 _ A _B_C_ . 3! 3 in A ile C yer değiş. yer değ. . 2! 4.6.2 48 Aralarda 2 kişinin olduğu bir seçenek olamaz. 7 kişi gerekirdi. Toplam 48 48 96 durum vardır. 96 96 Olasılık 6! 2 6 .5. 4 .3.2 2 buluruz. .1 15 49 4 fizik, 3 kimya ve 2 biyoloji öğretmeni bulunan bir okulda, bu öğretmenler arasından 3 kişilik Fen Bilimleri proje hazırlama ekibi kurulacaktır. Buna göre, bu ekipte her branş tan bir öğretmen bulunma olasılığı kaçtır? 1 2 3 3 5 A) B) C) D) E) 7 7 7 8 8 Çözüm: 9 9.8.7 72 Tüm durum 3 3! 12 .7 6 84 4 3 2 İstenen durum 4.3.2 24 1 1 1 24 Olasılık 2 84 7 2 bulunur. 7 53

