Soru Sor sayfası kullanılarak Mutlak Değer konusu altında Nitelikli Mutlak Değer Problemi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
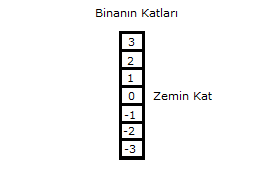
www.matematikkolay.net 7 katlı bir binada; katların 3 ü zemin katın üstünde, 3 ü zemin katın altındadır. A ve B herhangi iki kat , A B ve B A olduğuna göre; I. A katı zemin katın altında olabilir. II. A katı z emin katın üstünde olabilir. III. B katı zemin katın altında olabilir. IV. B katı zemin katın üstünde olabilir. Yargılarından hangileri doğrudur? Çözüm: A B ise A pozitif, B negatif olamaz. Diğer durumlar olabilir. Örneğin; 1 2 ; 2 1 ; 3 2; 2 3 gibi durumlar olabilirken 1 2 olamaz. |B| |A| ise A mutlak değerce daha büyük olmalıd ır. Yani yukarıdaki örnek durumlardan; 1 2 Bunlar olabilir. ; 2 1 ; 3 2; 2 3 Burdan anlıyoruz ki; A katı negatif olabiliyor. pozitif olamaz. B katı negatif veya pozitif olabilir. Bundan dolayı II. öncül hariç gerisi doğrudur. www.matematikkolay.net 27 a ve birer tam sayı olmak üzerei a 2 b 3 2 denklemini sağlayan kaç farklı (a, b) ikilisi vardır? A) 3 B) 6 C) 8 D) 10 E) 12 www.matematikkolay.net 0 2 Çözüm: |a 2| |b 3| 2 Mutlak değerin içi negatif olamaz. Bu sebeple, iki mutlak değerli ifadenin toplamı 2 ediyorsa Bunlar; 0 ve 2 1 ve 1 2 ve 0 olabilir. Şimdi bunları sırasıyla inceleyelim. |a 2| |b 3| 1 1 2 0 2 a 2 b 1 veya 5 2 farklı (a,b) ikilisi |a 2| |b 3| 2 a 1, 3 b 2 , 4 4 farklı (a,b) ikilisi |a 2| |b 3| 2 a 0, 4 b 3 2 farklı (a,b) ikilisi Toplam 8 farklı (a,b) ikilisi vardır. 71

