Soru Sor sayfası kullanılarak Mutlak Değer konusu altında Mutlak Değerli İfadenin en büyük, en küçük değeri, kaç farklı değeri vardır ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU

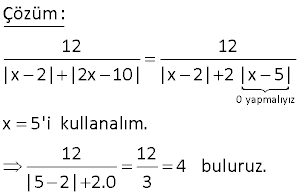
2.SORU


3.SORU


4.SORU
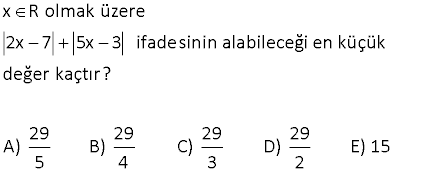

5.SORU


6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


12.SORU
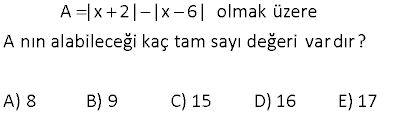

13.SORU
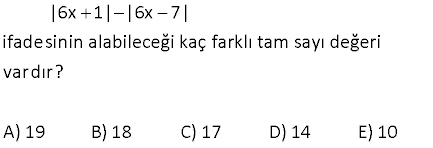

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
12 x 2 2x 10 ifadesinin en büyük değeri kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 0 yapmalıyız Çözüm: 12 12 |x 2| |2x 10| |x 2| 2 |x 5| x 5’i kullanalım. 12 12 4 buluruz. |5 2| 2.0 3 17 www.matematikkolay.net a, b, c, d, e, f sıfırdan farklı gerçek sayılar olmak üzere, a b c d e f a b c d e f ifadesinin alabileceği kaç farklı değer vardır? A) 15 B) 11 C) 8 D) 7 E) 4 Çözüm: a b c d e f |a| |b| |c| |d| |e| |f| ifadesinin alabileceği en büyük değer; 1 1 1 1 1 1 6 dır. Biri 1 olursa 4 olur. İkisi 1 olursa 2 … en küçük değer de 6 olur. Buna göre 6 dan 6’ya kadar çift değerleri alır. 6 ( 6) Terim sayısı 1 6 1 7 buluruz. 2 22 x x olduğuna göre, 8 3x ifadesinin alabileceği üç farklı tam sayı değerinin toplamı en çok kaçtır? A) 15 B) 18 C) 21 D) 24 E) 27 Çözüm: x |x| ise x 0 dır. 8 3x in en büyük değeri x 0 için gerçekleşir. Buna göre; x 0 8 3x 8 dir. x sayısı, bir tam sayı olmak zorunda değil. Bu sebeple 8 3x’in 8’den küçük, en büyük değerleri 7 ve 6 olabilir. Değerler toplamı 8 7 6 21 buluruz. 48 x R olmak üzere 2x 7 5x 3 ifadesinin alabileceği en küçük değer kaçtır? 29 29 29 29 A) B) C) D) E) 15 5 4 3 2 www.matematikkolay.net Çözüm: |2x 7| |5x 3| Mutlak değerin içini 0 yapan x değerlerinden biri bu değerin en küçük değerini sağlar. 7 2x 7 0 ise x için inceleyelim. 2 7 35 35 6 |2x 7| |5x 3| 0 5 3 3 2 2 2 29 dir. 2 5x 3 0 ise 3 x için inceleyelim. 5 3 6 6 35 |2x 7| |5x 3| 2 7 0 7 5 5 5 29 29 dir. Bu değer, diğerinden daha küçük o 5 5 29 olduğundan Cevap : tir. 5 55 www.matematikkolay.net A(x) x 2 x 4 ifadesinin alabileceği kaç fark – lı tam sayı değeri var dır? A) 14 B) 13 C) 12 D) 11 E) 10 0 olsun. Çözüm: A(x) |x 2| |x 4| Mutlak değerin içini 0 yapan değerler kritik noktalardır. Tüm ifadenin alabileceği maksimum ve minimum değerleri buradan bulabiliriz. |x 2| |x 4| x 2 0 x 2 0 2 4 6 0 olsun. 6 (minimum değer) |x 2| |x 4| x 4 0 x 4 4 2 0 6 6 (maksimum değer) A(x) |x 2| |x 4| ifadesi 6 ile 6 arasındaki tüm değerleri de alır. A(x)’in tam sayı değerleri sayısı; 6 ( 6) 1 12 1 1 13 bulunur. 56 |x y| 5 |x| | y| ifadesinin en büyük değeri ile en küçük değerinin toplamı kaçtır? A) 6 B) 10 C) 11 D) 12 E) 13 www.matematikkolay.net Çözüm: |x y| 5 |x| | y| x ve y pozitif olduğunda, en büyük değerini alır. |x y| x y 5 5 5 1 6 buluruz. |x| | y| x y x y olsun, en küçük değerini alır. |x y| 0 5 5 5 0 5 buluruz. |x| | y| |x| | y| Toplaml arı 6 5 11 buluruz. 69 6x 1 6x 7 ifadesinin alabileceği kaç farklı tam sayı değeri vardır? A) 19 B) 18 C) 17 D) 14 E) 10 www.matematikkolay.net Çözüm: Minimum değer; 6x 1 için; |6x 1| |6x 7| 0 | 1 7| 0 8 8 dir. Maksimum değer; 6x 7 için; |6x 1| |6x 7| |7 1| |7 7| 8 0 8 dir. 8’den 8’e kadar terim sayısı; 8 ( 8) 1 16 1 17 dir. 1 70 A x 2015 x 2015 olmak üzere A’nın alabileceği kaç farklı tam sayı değeri var dır? A) 1 B) 2015 C) 4030 D) 8060 E) 8061 www.matematikkolay.net Çözüm: En küçük değerini, x 2015 te alır. Bu değer için; A x 2015 x 2015 4030 dur. En büyük değerini, x 2015 te alır. Bu değer için; A x 2015 x 2015 4030 dur. 4030 dan 4030’a kadar Terim Sayısı 4030 ( 4030)1 8061 buluruz. 76 www.matematikkolay.net 2y 3x 9 x 6 y ifadesinin en büyük değeri kaçtır? 1 2 4 A) B) C) 1 D) E) 3 3 3 3 Çözüm: 2y 3x 2y 3x 9 x 6 y 3 3 x 2 y Not : a b a b dır. Payda küçüldükçe ifade büyür.O halde; 2y 3x 2y 3x 3 3 x 2 y 3 2y 3x 2y 3x 1 bulunur. 3 3 x 2 y 3 1 İfadenin en büyük değeri ‘ tür. 3 78 x R iken, y x 4 x 4 2x olduğuna göre, y’nin alabileceği tamsayı değerlerinin toplamı kaç – tır? A) 10 B)15 C) 21 D) 28 E) 36 www.matematikkolay.net negatif pozitif y Çözüm: 4 x 0 olduğundan; y |x 4| |x 4| 2x x 4 x 4 2x 8 2x tir. 4 x 0 idi. Her tarafı 2 ile çarpalım. 8 2x 0 Her tarafa 8 ekleyelim. 0 8 2x 8 y’nin değerleri 1,2,3,4,5, 6,7 Toplamları 28 dir. 51 a reel sayı olmak üzere, a 3 a 5 ifadesi kaç farklı tamsayı değeri alır? A) 17 B) 10 C) 9 D) 7 E) 2 negatif negatif Çözüm: |a 3| |a 5| ifadesi a’nın 3 farklı durumu için farklı değerler alır. 1.durum: a 5 için |a 3| |a 5| (a 3) ( (a 5)) a 3 a 5 8 dir. 2.durum: 5 a 3 içi negatif pozitif pozitif pozitif n |a 3| |a 5| a 3 (a 5) a 3 a 5 2a 2 dir. 5 a 3 aralığı için 8 ile 7 dahil bu aradaki tam sayı değerlerini alabilir. 3.durum: a 3 için |a 3| |a 5| a 3 (a 5) a 3 a 5 8 dir. Buna göre ifadenin alabileceği değer aralığı, 8 ile 8 dahil aradaki tam sayılardır. 8 ( 8) Terim Sayısı 1 17 buluruz. 1 www.matematikkolay.net 9 A |x 2| |x 6| olmak üzere A nın alabileceği kaç tam sayı değeri vardır? A) 8 B) 9 C) 15 D) 16 E) 17 Çözüm: A |x 2| |x 6| x 2 için; A 0 | 2 6| 0 8 8 dir. x 6 için; A |6 2| |6 6| 8 0 8 dir. 8 ile 8 arasında bunlar dahil; 8 ( 8) terim sayısı 1 17 sayı var dır. 1 37 |6x 1| |6x 7| ifadesinin alabileceği kaç farklı tam sayı değeri vardır? A) 19 B) 18 C) 17 D) 14 E) 10 www.matematikkolay.net 0 olsun Çözüm: |6x 1| |6x 7| Mutlak değerin içini 0 yapan değerler kritik noktalardır. Tüm ifadenin alabileceği maksimum ve mini – mum değerleri buradan bulabiliriz. |6x 1| |6x 7| (6x 1) | 0 olsun 0| | 1 7| 0 8 8 (minimum değer) |6x 1| |6x 7| (6x 7) |7 1| 0 8 0 8 (maksimum değer) 8 ile 8 dahil, aradaki tüm tam sayılar elde edilebilir. Buna göre; 8 ( Terim Sayısı 8) 1 16 1 17 farklı tam sayı 1 vardır. 44


Gerçekten çok faydalı bir içerik olmuş, hazırlayanların ellerine sağlık 👏🏻 Hiç bir yerde bulamadığım bazı soru tarzlarının anlatımlarını buldum sayenizde, teşekkürler!