Soru Sor sayfası kullanılarak Mutlak Değer konusu altında Mutlak değer parantezine alma soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU
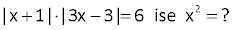

5.SORU
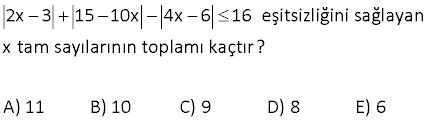
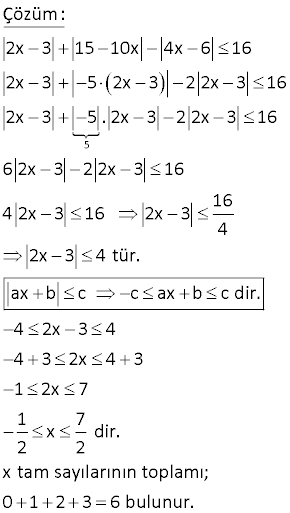
6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
x 2 3x 6 8 denkleminin çözüm kümesi aşağıdakilerden hangisidir? A) B) 0, 4 C) 0, 2 D) 0, 2 E) 2 Çözüm: |x 2| | 3x 6| 8 eşitliğini ortak paranteze almaya çalışalım. |x 2| |( 3)(x 2)| 8 |x 2| |( 3).(x 2)| 8 |x 2| 3.|x 2| 8 4.|x 2| 8 |x 2| 2 x 2 2 veya x 2 2 dir. x 4 x 0 Çözüm Kümesi {0,4} buluruz. 14 2 x 25 x 5 eşitliğini sağlayan x değerlerinin toplamı kaçtır? A) 5 B) 7 C) 8 D) 10 E) 11 www.matematikkolay.net 2 Çözüm: |x 25| x 5 |x 5||x 5| x 5 |x 5| |x 5| x 5 x 5 denklemi sağlar. |x 5| 1 x 5 1 x 4 veya; x 5 1 x 6 Ancak, x 5′ ten küçük olamaz. zorundadır. Çünkü ilk eşitlikte, mutlak değerli ifade pozitif dışarı çık ar. Buna göre tek çözüm x 5 tir. 20 |x 2| |3x 6| |2 x| 25 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisi – dir? A) [ 3, 7] B) [ 3, 5] C) [ 5, 5] D) [5, 7] E) [ 3, 6] Çözüm: |x 2| |3x 6| |2 x| 25 |x 2| ile |2 x| aynı şeydir. Buna göre; |x 2| 3|x 2| |x 2| 25 şeklinde yazabiliriz. 5|x 2| 25 |x 2| 5 5 x 2 5 her tarafa 2 ekleyelim. 3 x 7 Ç.K. [3,7] buluruz. 33 |x 1||3x 3| 6 ise x2 ? 2 2 2 2 2 Çözüm: |x 1| |3x 3| 6 |x 1|.3|x 1| 6 |x 1||x 1| 2 |x 1| 2 x 1 2 x 3 buluruz. (x 1 2 x 1 olamaz.) 38 2x 3 15 10x 4x 6 16 eşitsizliğini sağlayan x tam sayılarının toplamı kaçtır? A) 11 B) 10 C) 9 D) 8 E) 6 www.matematikkolay.net 5 Çözüm: 2x 3 15 10x 4x 6 16 2x 3 5 2x 3 2 2x 3 16 2x 3 5 . 2x 3 2 2x 3 16 6 2x 3 2 2x 3 16 16 4 2x 3 16 2x 3 4 2x 3 4 tür. ax b c c ax b c dir. 4 2x 3 4 4 3 2x 4 3 1 2x 7 1 7 x dir. 2 2 x tam sayılarının toplam ı; 0 12 3 6 bulunur. 79 x 4 x 3 x 4 denklemini sağlayan x değer – lerinin toplamı kaçtır? A) 10 B) 6 C) 4 D) 2 E) 1 www.matematikkolay.net Çözüm: x 4 x 3 x 4 x 4 leri sadeleştirebiliriz. Eşitliğin her iki tarafını 0 yapan x 4 kökünü unutmayalım. x 4 x 3 x 4 x 3 1 dir. x 3 1 x 1 3 4 tür. x 3 1 x 1 3 2 dir. Tüm köklerin toplamı 4 4 2 2 buluruz.

