Soru Sor sayfası kullanılarak Mutlak Değer konusu altında İki mutlak değerin eşitsizliği ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
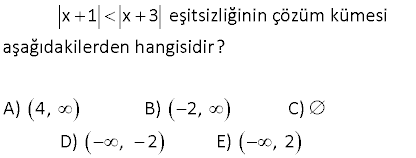

2.SORU
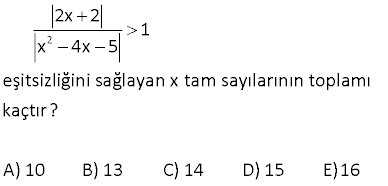

3.SORU
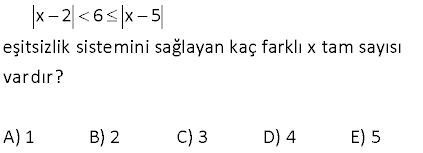
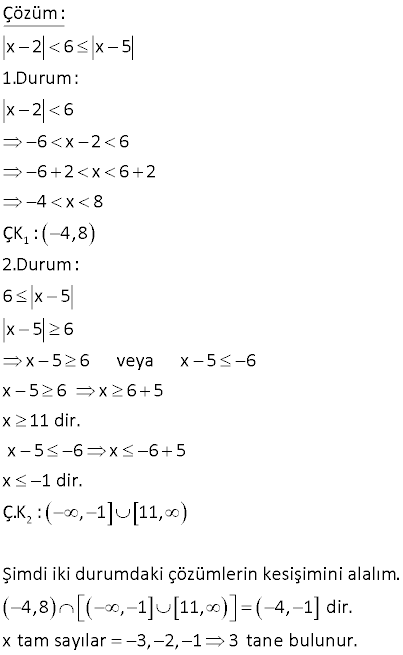
4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
x 1 x 3 eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir? A) 4, B) 2, C) D) , 2 E) , 2 www.matematikkolay.net Çözüm: x’in 3 farklı durumuna göre soruyu inceleyelim. 1.durum: x 3 ise mutlak değerli ifadelerin içi negatif olacaktır. Buna göre; |x 1| |x 3| x 1 x 3 1 3 1, 3′ ten küçük değildir. Burda negatif pozitif çözüm yok. 2.durum: 3 x 1 ise |x 1| |x 3| x 1 x 3 2x 4 iki tarafı da 2′ ye bölelim. Eşitsizliği ile böldüğümüz işin eşitsizlik yön değiş – pozitif pozitif tirir. x 2 buluruz. 3.durum: x 1 ise |x 1| |x 3| x 1 x 3 1 3 her zaman sağlanır. Tüm çözümleri toplarlarsak, 2’den büyük değerler için çözümün sağlandığını görüyoruz. Çözüm Kümesi (2,) buluruz. www.matematikkolay.net 13 2 2x 2 1 x 4x 5 eşitsizliğini sağlayan x tam sayılarının toplamı kaçtır? A) 10 B) 13 C) 14 D) 15 E)16 2 Çözüm: 2x 2 1 x 4x 5 2 x 1 x 5 . x 1 1 2 x 5 2 x 5 2 2 5 x 2 5 3 x 7 Bu aralıktaki 5 dışındaki tüm değerler denklemi sağlar. 5′ paydayı 0 yaptığı için tanımsızlık getireceğinden alınmaz. 4 6 10 bulunur. www.matematikkolay.net 35 x 2 6 x 5 eşitsizlik sistemini sağlayan kaç farklı x tam sayısı vardır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 1 2 Çözüm: x 2 6 x 5 1.Durum: x 2 6 6 x 2 6 6 2 x 6 2 4 x 8 ÇK : 4,8 2.Durum: 6 x 5 x 5 6 x 5 6 veya x 5 6 x 5 6 x 6 5 x 11 dir. x 5 6 x 6 5 x 1 dir. Ç.K : , 1 11, Şimdi iki durumdaki çözümle rin kesişimini alalım. 4,8 , 1 11, 4, 1 dir. x tam sayılar 3, 2, 1 3 tane bulunur. 66 |x| 5 0 eşitsizliğini sağlayan x tam sayıları |x 4| toplamı kaçtır? A) 4 B) 3 C) 0 D) 3 E) 4 Çözüm: |x| 5 0 Payda daima pozitif olacağından, |x 4| pay kısmı negatif olmalıdır. |x| 5 0 5 x 5 x 4, 3, 2, 1, 0, 1, 2, 3, 4 olabilir. Ancak, payda 0 0 olamayacağı için x 4 olamaz. Buna göre; değerler toplamı; 4 3 2 1 0 1 2 3 4 buluruz. 77


Teşekkür ederim yardımınız için.