Soru Sor sayfası kullanılarak Mutlak Değer konusu altında İç içe mutlak değerler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
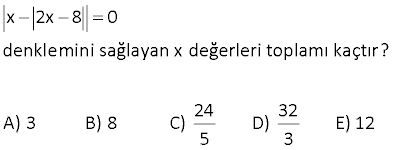

2.SORU


3.SORU
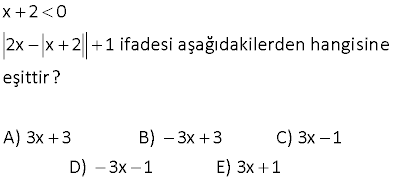
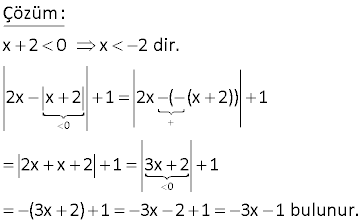
4.SORU
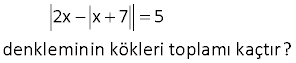

5.SORU


6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net x 2x 8 0 denklemini sağlayan x değerleri toplamı kaçtır? 24 32 A) 3 B) 8 C) D) E) 12 5 3 0 Çözüm: |x |2x 8|| 0 x |2x 8| 0 x |2x 8| x 2x 8 veya x 2x 8 x 8 3x 8 8 x 3 8 32 Değerler toplamı 8 buluruz. 3 3 3 7 x 1 k denkleminin farklı dört gerçel kökünün olması için k nin alabileceği kaç farklı tam sayı değeri var dır? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net Çözüm: 7 |x 21| k ya da 7 |x 21| k olabilir. 7 k |x 21| x 21 7 k x 28 k (1.değer) x 21 k 7 x k 14 (2.değer) 7 |x 21| k 7 k |x 21| 7 k x 21 x 28 k (3.değer) 7 k x 21 x 14 k (4.değer) Bulduğumuz 4 değer birbirine eşit olmamalıdır. k için 28 k k 14 28 k 14 k k 0 için 28 14 28 14 (Aynı var ) k 1 için 27 15 29 13 k 2 için 26 16 30 12 …. k 6 için 22 30 34 8 k 7 için 21 21 35 7 (Aynı var) k’nın 1,2,..,6 değerleri için x farklı değerler alabiliyor. 19 x 2 0 2x x 2 1 ifadesi aşağıdakilerden hangisine eşittir? A) 3x 3 B) 3x 3 C) 3x 1 D) 3x 1 E) 3x 1 0 0 Çözüm: x 2 0 x 2 dir. 2x x 2 1 2x ( (x 2)) 1 2x x 2 1 3x 2 1 (3x 2) 1 3x 2 1 3x 1 bulunur. www.matematikkolay.net 32 2x x 7 5 denkleminin kökleri toplamı kaçtır? www.matematikkolay.net Çözüm: 1.durum: 2x |x 7| 5 2x 5 |x 7| 1.a) 2x 5 x 7 x 12 1.b) (2x 5) x 7 2x 5 x 7 3x 2 2 x 3 2.durum: 2x |x 7| 5 2x 5 |x 7| 2.a) 2x 5 x 7 x 2 2.b) (2x 5) x 7 2x 5 x 7 3x 12 x 4 Toplamda 4 farklı kök bulduk, bunları asıl denklemde tekrar test etmek gerekiyor. |2x |x 7|| 5 12 ve 2 sağlark en; diğer kökler sağlamıyor. Kökler toplamı 12 2 14 buluruz. www.matematikkolay.net 34 x 3 4 a denklemini sağlayan dört farklı x gerçek sayısı olduğuna göre a’nın değer aralığı aşağıdakilerden hangisidir? A) [ 4,0] B) ( 4,2) C) (2,4) D) (0,4) E) [ 4,4] www.matematikkolay.net x 3 4 a Mutlak değerli ifade negatif olamaz. a 0 olsa 4 farklı çözüm olamaz. a 0 dır. x 3 4 a veya x 3 4 a dır. x 3 a 4 veya x 3 a 4 bu iki ifadeden de 2’şer kök gelebilmesi için; a 4 0 a 4 olmalı . a 0 bulmuştuk zaten. ve a 4 0 olmalı a 4 a 4 olur. 0 a 4 a 0,4 bulunur. 42 n, 3’ten büyük doğal sayıdır. x 2x 3x … nx n … 3 2 1 40n 10 denklemini sağlayan kaç farklı x doğal sayısı var dır? A) 10 B) 9 C) 8 D) 7 E) 6 www.matematikkolay.net Çözüm: x 2x 3x … nx n … 3 2 1 40n 10 x 1 2x 2 3x 3 … nx n 40n 10 x 1 2 x 1 3 x 1 … n x 1 40n 10 kaç farklı x doğal sayısı var diye sorduğuna göre; x kesinlikle negatif olamaz.Yani mutlak değer dışına direk çıkar. İfade birden n’e kadar x 1 lerin toplamı olur. n(n 1) (x 1) 40n 10 2 80n 20 60 20 x 1 n(n 1) n 1 n Sorunun bu hali sadece n 4 ve n 5 için sağlanır ve 2 tane x değeri bulunur.biz 40n 10 ifadesinin 40n 40 olabileceğini düşündük. n(n 1) (x 1) 40n 40 2 n(n 1) .(x 1) 80 (n1) 80 n x 1 x 0,1,3,4,7,9,15,19 değerlerini alabilir. 8 tane x değeri bulunur. www.matematikkolay.net 46

