Soru Sor sayfası kullanılarak Limit konusu altında Çarpanlarına ayırarak, eşlenikle çarparak limit bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
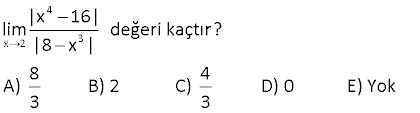

2.SORU
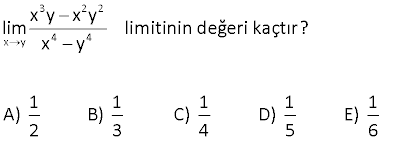
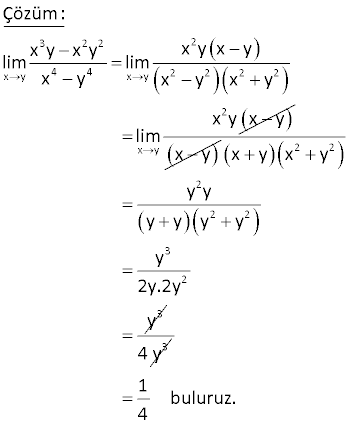
3.SORU
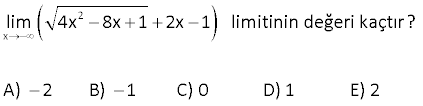
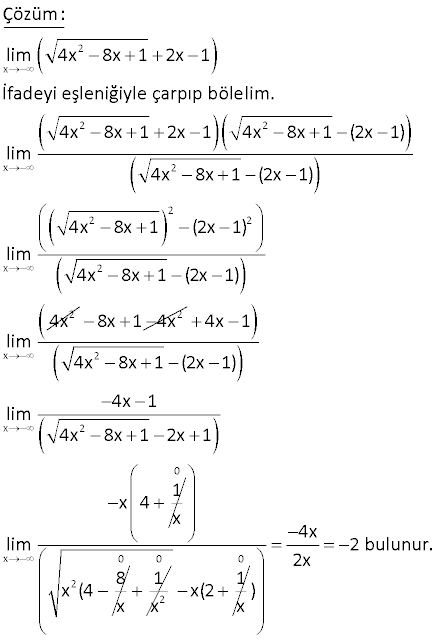
4.SORU
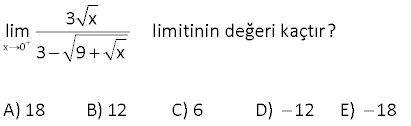
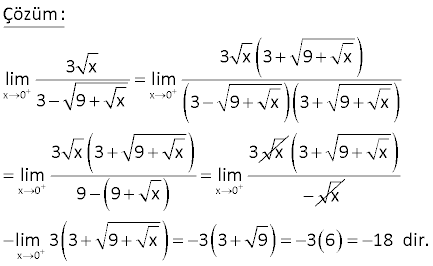
5.SORU
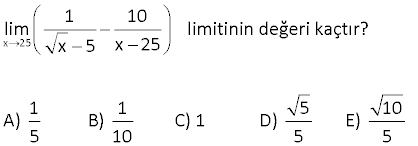
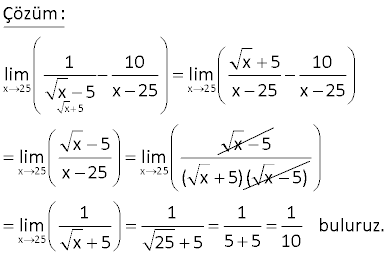
6.SORU
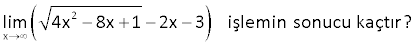
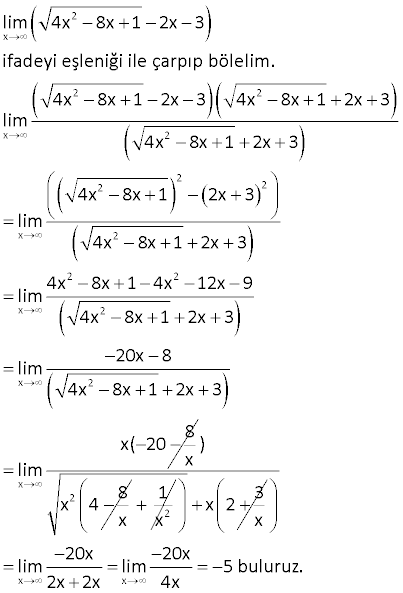
7.SORU
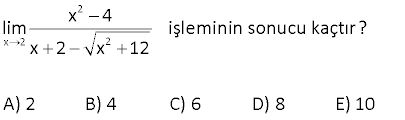
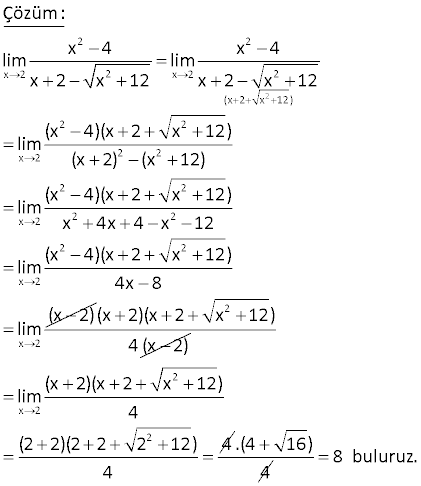
8.SORU
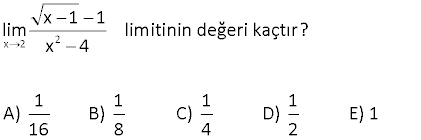
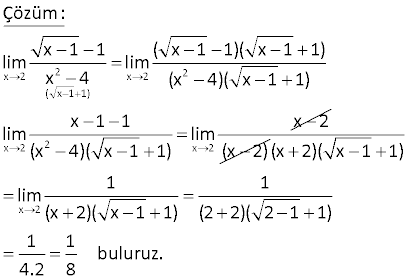
9.SORU
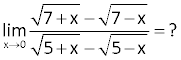
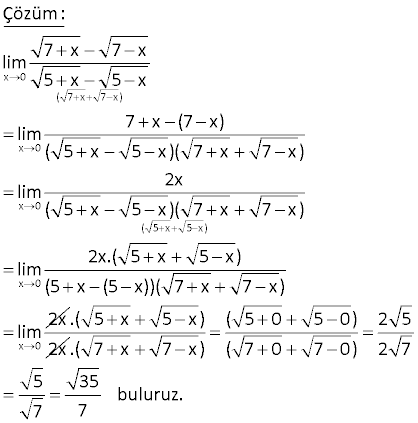
10.SORU
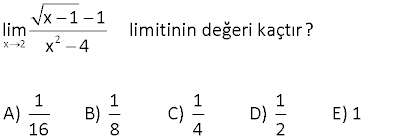
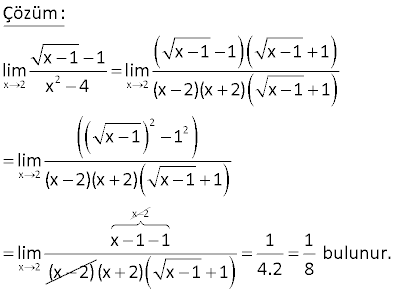
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net 4 x 2 3 |x 16| lim değeri kaçtır? |8 x | 8 4 A) B) 2 C) D) 0 E) Yok 3 3 4 4 x 2 3 x 2 3 3 2 2 x 2 2 x 2 Çözüm: |x 16| |x 16| İki kare farkı lim lim |8 x | |2 x | İki küp farkı |x 4|.|x 4| lim |2 x||4 2x x | |x 2| lim 2 |x 2|.|x 4| |2 x| 2 2 x 2 2 2 2 |x 2| |2 x| |4 2x x | |x 2|.|x 4| lim |4 2x x | |2 2|.|2 4| 4.8 32 |4 2.2 2 | |4 4 4| 8 12 3 8 buluruz. 3 49 www.matematikkolay.net 3 2 2 x y 4 4 x y x y lim limitinin değeri kaçtır? x y 1 1 1 1 1 A) B) C) D) E) 2 3 4 5 6 3 2 2 2 x y 4 4 x y 2 2 2 2 2 x y Çözüm: x y x y x y x y lim lim x y x y x y x y x y lim x y 2 2 2 2 2 3 2 3 x y x y y y y y y y y 2y.2y y 3 4 y 1 buluruz. 4 82 2 x lim 4x 8x 1 2x 1 limitinin değeri kaçtır? A) 2 B) 1 C) 0 D) 1 E) 2 www.matematikkolay.net 2 x 2 2 x 2 2 2 2 x 2 2 x Çözüm: lim 4x 8x 1 2x 1 İfadeyi eşleniğiyle çarpıp bölelim. 4x 8x 1 2x 1 4x 8x 1 (2x 1) lim 4x 8x 1 (2x 1) 4x 8x 1 (2x 1) lim 4x 8x 1 (2x 1) 4x lim 2 8x 1 4x 2 x 2 x 4x 1 4x 8x 1 (2x 1) 4x 1 lim 4x 8x 1 2x 1 1 x 4 x lim 0 2 8 x (4 x 0 2 1 x 0 1 x(2 x 0 4x 2 bulunur. 2x ) 71 www.matematikkolay.net x 0 3 x lim limitinin değeri kaçtır? 3 9 x A) 18 B) 12 C) 6 D) 12 E) 18 x 0 x 0 x 0 x 0 Çözüm: 3 x 3 9 x 3 x lim lim 3 9 x 3 9 x 3 9 x 3 x 3 9 x 3 x lim lim 9 9 x 3 9 x x x 0 lim 3 3 9 x 3 3 9 3 6 18 dir. Buraya kadar siteye yüklendi. SORU www.matematikkolay.net a)Fonskiyonun süreksiz olduğu noktalar limitin olmadığı ve o noktadaki değerinin limite eşit olmadığı noktalardır. Grafiğe bakılırsa; x 1 ve x 2 noktalarında limit yoktur.Fonksiyon bu noktalarda sürek x 0 x 2 2 sizdir. 1 2 1 dir. b)limf(x) 2 dir.Grafikte kopma olmadığı için sağdan soldan bakmaya gerek yok. c) lim(fof)(x) f(f(2 )) f(2) 0 dır. www.matematikkolay.net x 25 1 10 lim limitinin değeri kaçtır? x 5 x 25 1 1 5 10 A) B) C) 1 D) E) 5 10 5 5 x 25 x 25 x 5 x 25 x 25 Çözüm: 1 10 x 5 10 lim lim x 5 x 25 x 25 x 25 x 5 x 5 lim lim x 25 ( x 5) ( x 5) x 25 1 1 1 1 lim buluruz. x 5 25 5 5 5 10 18 2 x lim 4x 8x 1 2x 3 işlemin sonucu kaçtır? www.matematikkolay.net 2 x 2 2 x 2 2 2 2 x 2 2 2 x 2 x 2 lim 4x 8x 1 2x 3 ifadeyi eşleniği ile çarpıp bölelim. 4x 8x 1 2x 3 4x 8x 1 2x 3 lim 4x 8x 1 2x 3 4x 8x 1 2x 3 lim 4x 8x 1 2x 3 4x 8x 1 4x 12x 9 lim 4x 8x 1 2x 3 20x 8 lim 4x 8x x 1 2x 3 8 x( 20 x lim 2 ) 8 x 4 x 2 1 x 3 x 2 x x x 20x 20x lim lim 5 buluruz. 2x 2x 4x 19 2 x 2 2 x 4 lim işleminin sonucu kaçtır? x 2 x 12 A) 2 B) 4 C) 6 D) 8 E) 10 www.matematikkolay.net 2 2 2 x 2 2 x 2 2 (x 2 x 12) 2 2 x 2 2 2 2 2 x 2 2 2 2 2 x 2 x 2 Çözüm: x 4 x 4 lim lim x 2 x 12 x 2 x 12 (x 4)(x 2 x 12) lim (x 2) (x 12) (x 4)(x 2 x 12) lim x 4x 4 x 12 (x 4)(x 2 x 12) lim 4x 8 (x 2) lim 2 (x 2)(x 2 x 12) 4 (x 2) 2 x 2 2 (x 2)(x 2 x 12) lim 4 (2 2)(2 2 2 12) 4 4 .(4 16) 4 8 buluruz. 21 x 2 2 x 1 1 lim limitinin değeri kaçtır? x 4 1 1 1 1 A) B) C) D) E) 1 16 8 4 2 x 2 2 x 2 2 ( x 1 1) x 2 2 x 2 Çözüm: x 1 1 ( x 1 1)( x 1 1) lim lim x 4 (x 4)( x 1 1) x 1 1 x 2 lim lim (x 4)( x 1 1) (x 2) x 2 (x 2)( x 1 1) 1 1 lim (x 2)( x 1 1) (2 2)( 2 1 1) 1 1 buluruz. 4.2 8 www.matematikkolay.net 40 x 0 7 x 7 x lim ? 5 x 5 x www.matematikkolay.net x 0 ( 7 x 7 x ) x 0 x 0 ( 5 x 5 x ) x 0 x 0 Çözüm: 7 x 7 x lim 5 x 5 x 7 x (7 x) lim ( 5 x 5 x)( 7 x 7 x) 2x lim ( 5 x 5 x)( 7 x 7 x) 2x.( 5 x 5 x) lim (5 x (5 x))( 7 x 7 x) 2x lim .( 5 x 5 x) 2x ( 5 0 5 0) 2 5 .( 7 x 7 x) ( 7 0 7 0) 2 7 5 35 buluruz. 7 7 44 x 2 2 x 1 1 lim limitinin değeri kaçtır? x 4 1 1 1 1 A) B) C) D) E) 1 16 8 4 2 www.matematikkolay.net x 2 2 x 2 2 2 x 2 x 2 x 2 Çözüm: x 1 1 x 1 1 x 1 1 lim lim x 4 (x 2)(x 2) x 1 1 x 1 1 lim (x 2)(x 2) x 1 1 x 1 1 lim (x 2) 1 1 bulunur. (x 2) x 1 1 4.2 8 55

