Karşılaşmalı Sorular

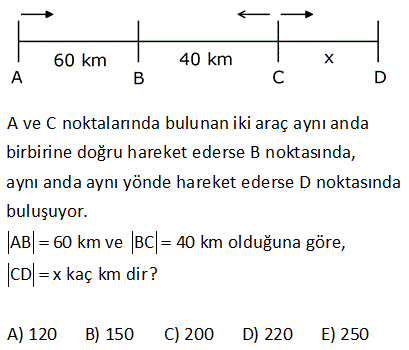
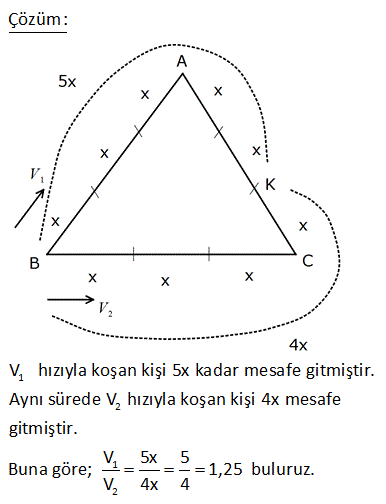
www.matematikkolay.net A kentinden B kentine doğru sabit hızla hareket eden bir otomobilin hızı, B kentinden A kentine doğru aynı anda yola çıkan motosikletlinin hızının 3 katıdır. Bu iki araç karşılaştıklarında otomobil hızını yarıya indirirken motosiklet iki katına çıkarıyor ve otomobil bu karşılaş – madan 60 dakika sonra B kentine varıyor. Motosiklet bu karşılaşmadan kaç dakika sonra A kenti – ne varır? A) 105 B) 120 C) 135 D) 150 E) 180 Çözüm: Motosikletin hızına V dersek, Otomobilin hızı 3V olur. Bu iki hareketli t süre sonra C noktasında karşılaşmış olsunlar. Buna göre; Motosikletin gittiği yol : BC V.t Otomobilin gittiği yol : AC 3.V.t   dir. www.matematikkolay.net Karşılaşmadan sonra Otomobil, hızını yarıya düşürünce 3V yeni hızı: olur. 2 Otomobilin B noktasına varması için Vt kadar yolu kal – mıştır. Bu yolu 60 dakikada aldığına göre; Vt Vt 2 60 60 3V 1 3V 2      Vt 2 1  3V  60 30 t 90 dakika bulunur. Motosikletin hızı iki katına çıkınca, hızı 2V olur. A noktasına varması için gideceği yol 3Vt kadardır. Buna göre; 3Vt 3 V 2V   t 2V 3t (t 90 idi) 2 3t 3.90 3.45 135 dakikada motosiklet A nokta- 2 2 sına varır. Doğru Cevap : C şıkkı      3 www.matematikkolay.net A ve C noktalarında bulunan iki araç aynı anda birbirine doğru hareket ederse B noktasında, aynı anda aynı yönde hareket ederse D noktasında buluşuyor. AB 60 km ve BC 40 km olduğuna göre, CD x kaç km di    r? A) 120 B) 150 C) 200 D) 220 E) 250 A A C C Çözüm: İlk durumda bir araç 60 km giderken, diğeri 40 km gidebilmiş. Burdan hızları oranını bulalım. V 60 3 V 3V , V 2V diyebiliriz. V 40 2 D’ye gittikleri durumda ise C’deki araç x kadar yol, A’da      ki araç ise x 100 km yol gitmiştir. Süreler aynı olduğunundan süreleri eşitleyen bir denklem yazalım. x 100 3V   x 2V  2x 200 3x x 200 km buluruz.    11 www.matematikkolay.net 1 2 ABC eşkenar üçgeninin her kenarı üç eşit parçaya bölünmüştür. İki koşucu A noktasından ters yönde üçgenin çevresi boyunca koşmaya başlamışlardır. İki koşucu K noktasında karşılaştıklarına göre, V or V anı kaçtır? A) 0,8 B) 1 C) 1,25 D) 1,5 E) 1,75 Çözüm: 1 2 1 2 V hızıyla koşan kişi 5x kadar mesafe gitmiştir. Aynı sürede V hızıyla koşan kişi 4x mesafe gitmiştir. V 5x 5 Buna göre; 1,25 buluruz. V 4x 4    www.matematikkolay.net 30 A ve B şehirlerinden hareket eden iki araç C’de karşılaştık tan sonra yollarına devam ediyorlar. A’dan hareket eden karşılaşma anından 4 saat sonra B’ye vardığında, B’den hareket edeni 5 saatlik yolu kalıyor. AB 300 km olduğuna göre, yavaş giden aracın hızı saatte kaç kilometredir? A) 50 B) 40 C) 30 D) 20 E) 15  www.matematikkolay.net 1 1 2 1 2 2 Çözüm: C ile B arasını V ile giden araç 4 saatte alıyorsa; |CB| 4V dir. V ile hareket eden araç ise bu me- 4V safeyi sürede geçip C noktasında 1.araçla kar V şılaşmıştır. A ile C arasını V ile gide  2 1 2 1 1 2 2 1 n araç toplam 9 saatte alıyorsa; |AC| 9V dir. V ile hareket eden araç ise 9V bu mesafeyi sürede geçip C noktasında V 2.araçla karşılaşmıştır. Bu iki süreyi birbirine eşitleyelim. 4V 9V 4 V V    2 2 1 2 1 2 1 2 1 2 3k 2k 2 V 9V V 3k V 2k dır. 4V 9V 300 ise 4V 9V 300 4.3k 9.2k 300 12k 18k 300 30k 300 k 10 dur. V 2k 2.10 20 buluruz.                   31 A ve B noktaları arası 500 m dir. A ve B noktalarından hızları 4v m / dk ve (3v 20) m / dk olan iki hareketli birbirine doğru aynı anda hareket ettikten 5 dakika sonra aralarındaki uzaklık 2400 m oluyor.  Buna göre, bu hareketlilerin hızları farkı kaç m/ dk dır? A) 80 B) 75 C) 70 D) 65 E) 60 www.matematikkolay.net Çözüm: Bu iki hareketli, ilk önce aradaki 500 metre mesafe – yi bitirmişler; daha sonra da birbirlerinden 2400 m mesafe uzaklaşmışlardır. Yani toplamda 2900 metre mesafe gitmişlerdir. Buna göre; 2900  5.(4v  3v 20) 2900 5.(7v 20) 2900 35v 100 2800 35v 2800 v 80 dir. 35 Hızları farkı 4v (3v 20) 320 (240 20) 320 260 60 buluruz.                  36 www.matematikkolay.net Hızı saatte 90 km olan bir hareketli A noktasından, hızı saatte 40 km olan diğer bir hareketli B noktasından aynı anda birbirlerine doğru hareket ediyorlar. AC x km ve BC y km dir. A’dan hareket eden   araç B’ye gidip hiç durmadan geri döndüğünde, diğer araçlar C de karşılaştığına x göre, oranı kaçtır? y 1 4 3 A) B) 1 C) D) E) 2 4 3 2 Çözüm: Bu karşılaşma t süre sonra gerçekleşmiş olsun. Yavaş olan araç 40t yol gitmiştir. y 40t dir. Hızlı olan araç 90t yol gitmiştir. 90t x y y 90t x 40t 40t 90t x 80t x 10t dir. x 10t 1 Buna göre; b y 40t 4             uluruz. 58 İs tanbul’dan Rize’ye aynı yol üzerinden otobüs 18 saatte, kamyon 30 saatte gitmektedir. Otobüs İs tanbul’dan, kamyon Rize’den saatte 07.45 te karşılıklı olarak aynı anda hareket ederlerse saat kaçta karşılaşırlar? A) 17.45 B) 18.00 C) 18.15 D) 18.30 E) 19.00 (5) (3) Çözüm: 1 1 1 5 3 1 8 1 18 30 t 90 90 t 90 t 90 t saat sonra karşılaşırlar. 8 90 Dakika olarak 60 675 dakika eder 8 Yani 11 saat 15 dakika 07: 45 11:15 19: 00 buluruz.               62 www.matematikkolay.net Eşkenar üçgen şeklindeki bir koşu pistinde A noktasından hareket eden koşucu aynı noktaya 1 dakika sonra, C noktasından hareket eden koşucu aynı noktaya 3 dakika sonra gelmektedir. Aynı anda ve aynı yönde şekildeki gibi A ve C den hareket eden koşucular kaç dakika sonra A noktasında ilk kez buluşur? A) 5 B) 4 C) 3 D) 2 E) 1 Çözüm: A koşucusu 1 dakikada bir A noktasından geçer. C koşucusu ilk defa 2.dakikada A noktasından geçer. Dolayısıyla 2.dakikada A’da karşılaşmış olurlar. Cevap: 2 63 www.matematikkolay.net A kentinden ortalama hızı saatte 100 km, B kentinden ortalama hızı saatte 80 km olan iki araç aynı anda birbirine doğru hareket ettikten 4 saat sonra karşılaşıyorlar. A kentinden hareket eden araç B kentine ulaş – tığında B kentinden arkadan araç A kentinden kaç km uzaktadır? A) 120 B) 144 C) 150 D) 164 E) 170 Çözüm: |AB| 4.(100 80) 4.180 720 km dir. 720 A aracı bu yolu 7,2 saatte bitirir. 100 B aracı 7,2 saatte 80.7,2 576 km gider. Geriye kalan yol 720 576 144 km buluruz. Cevap: 144           64 A ve C noktalarındaki iki araç aynı anda birbirle – rine doğru hareket ederlerse B de, aynı yönde hareket ederlerse D de karşılaşıyorlar. AB 30 km ve CD 20 km olduğuna göre, B ile C arası kaç km dir? A) 10   B) 20 C) 30 D) 50 E) 60 www.matematikkolay.net C A C A A C C A A A C C A C A C 10 Çözüm: |BC| x diyelim. 30 30V (V V ) 30 x 30 30 x V V 30V V x x dur. V V 30 20 (V V ). 30 x V 20V 20 30 x V 20V 20.30 x 50 x 50 V x 600 x 50 x 600 x (x 5                                60 0)  x 10 buluruz. 69 Birbirinden 48 km uzaklıkta olan A ve B noktalarından aynı anda ve birbirine doğru harekete 4 başlayan iki araç saat sonra karşılaşıyorlar. 3 Buna göre, iki araç tan yalnızca biri saatteki hızını kaç km arttırırsa karşılaşma araçlarının hareket – lerinden 1 saat sonra gerçekleşir? A) 16 B) 12 C) 10 D) 9 E) 8 www.matematikkolay.net   1 2 t t Çözüm: İki araç birbirlerine doğru geliyorsa hızları toplanır. Yol V V .t 4 48 V . 3 3 V 48 36 km/ sa 4 Araçlardan biri hızını x km artırırsa hızları toplamı 36 x olur Karşılaşma hareketten 1 saat sonra gerçe           kleşiyorsa t 1 olur. 48 36 x .1 x 12 km/ sa bulunur.      71 www.matematikkolay.net 1 2 İki koşucu A noktasından aynı anda koşmaya başlıyor. birisi AB yönünde V hızı ile diğeri AD yönünde V hızı ile ABCD dikdörtgeninin çevresinde koşuyorlar ve ilk kez [BC] nin orta noktasına olan E nokta 1 2 sında karşılaşıyorlar. V AB 2 AD olduğuna göre, oranı kaçtır? V 3 4 5 5 7 A) B) C) D) E) 4 5 7 6 8  1 2 Çözüm: Aynı sürede gidilen yolları oranlamak yeterli olacaktır. Dikdörtgenin uzun kenarına 4 birim, kısa kenarına da 2 birim diyelim. V 4 1 5 buluruz. V 2 4 1 7      84 A ve B noktalarından hızları saatte V 45 km ve V km iki araç birbirlerine doğru aynı anda hareket ediyorlar ve C de karşılaşıyor. AB 5 BC olmak üzere B den hareket eden araç C den A ya 8 saatte gittiğine   göre, A ile B arasın – daki uzaklık kaç km dir? A) 150 B) 140 C) 120 D) 100 E) 80 www.matematikkolay.net Çözüm: |BC| x dersek |AC| 4x olur. V 45 4 x V     x V 45 4V 3V 45 V 15 |AC| 15.8 120 km dir. 4x 120 x 30 |AB| 5x 5.30 150 km dir.                 86 www.matematikkolay.net 1 2 ABC eşkenar üçgendir. Üçgenin A köşesinden hızı saatte V km olan araç B’ye doğru, hızı saatte V km olan araç C ye doğru aynı anda harekete başlıyor ve ilk kez [BC] üzerindeki D noktasında karşılaşıyo 1 2 1 rlar. V V 270 ve BD 2 DC olduğuna göre V kaçtır? A) 170 B) 160 C) 150 D) 120 E) 100    Çözüm: www.matematikkolay.net 1 2 1 2 1 2 1 İki araç D noktasında karşılaştığında V hızlı araç, 5k, V hızlı araç, 4k yol almıştır.Hız ile alınan yol ters orantılı olduğundan; V 5V ve V 4V olur. V V 270 5V 4V 9V 270 V 30 V 5V 5.30              150 bulunur. 91 BD 3x km dir. A ve B deki araçlar birbirine doğru hareket ederlerse C de, aynı yönde hareket ederlerse D de buluştuklarına göre x in eşiti nedir? A) AC 8 4 B 0 km, CB 2x ) 5 C) 8 D) km 10 E , ) 20    www.matematikkolay.net A B Çözüm: Birbirlerine doğru hareket ettiklerinde; 80 2x 80 V V   40 A 2 V  A B B A B A B A x xV V tır. V 40 Aynı yönde hareket ettiklerinde; 80 5x 3x xV V yazalım V V 40 80 5x V             3x  x A V 3 80 5x 80 5x 120 1 40 40 5x 40 x 8 buluruz.           102 Şekilde gösterilen A ve C noktalarından aynı anda hareket eden iki araç birbirine doğru gittiklerinde B de, aynı yönde gittiklerinde ise D de buluşu – yorlar. Şekilde verilen uzunluklara göre, BC x kaç k  m dir? A) 15 B) 16 C) 18 D) 20 E) 22 www.matematikkolay.net A C A C A C A C A Çözüm: Birbirlerine doğru hareket ettiklerinde; 30 x xV V dur. V V 30 Aynı yönde hareket ettiklerinde; 130 x 100 100V V yazalım V V 130 x 100 V              A x V 130 x   2 2 150.( 20) 3000 130x x 30 0 x 130x 3000 0 (x 150)(x 20) x 20 buluruz.               119 1 2 ABCD kare şeklinde bir pist olmak üzere iki bisikletli şekildeki A noktasından aynı anda harekete başlıyorlar. Bisikletlilerin hızları oranı V 2 olmak üzere, hareketliler 2.kez nerede V 3 karşılaşırlar  ? A) B noktası B) C noktası C) A B arası D) A noktası E) D noktası  www.matematikkolay.net 1 2 1 Çözüm: V 2V, V 3v olsun. Pistin uzunluğu 4 br olsun. 4 İlk buluşmaları sonra ikinci buluşmaları da 5V 8 sonra olur.Birbirlerine doğru geldikleri için 5V hızlar toplandı. V hızlı bisikletli bu sürede; 8 5V   2 V 16 br 3,2 br yol gider. 5 Pist 4 br di. Karşılaşma A ile B arasında gerçekleşir.   121 Bir parkta Ali ile Burcu sırasıyla A ve B noktaların – dan birbirine doğru aynı anda koşmaya başlamıştır. Karşılaşmalarından 9 dakika sonra Ali, B noktasına varmıştır. Ali, B’ ye var dık tan 7 dakika sonra da Burcu A noktasına ulaşmıştır. Buna göre, Ali ve Burcu koşuya başladık tan kaç dakika sonra karşılaşmıştır? A) 6 B) 8 C) 10 D) 12 E) 15 www.matematikkolay.net Çözüm: AC arası x m olsun BC arası y m olsun Ali ve Burcu t dakika sonra C noktasında karşılaşsın. Ali t dakikada x m yol alırsa, Burcu t dakikada y m alır. Ali y m yi 9 dakikada gidiyorsa, Burcu x m yi 16 dakik     2 2 ada alır. x Alinin hızı: t y Burcunun hızı t x 9 y I t y 16 x tir. II t İlk denklemde x yerine ikinci denklemdeki eşitini yazalım. y 16.9 y t t 16.9 t 4.3 12 dk bulunur.           135 www.matematikkolay.net A kentinden B kentine doğru sabit hızlı hareket eden bir otomobilin hızı, B kentinden A kentine doğru aynı anda yola çıkan motosikletin hızının 3 katıdır. Bu iki araç karşılaştıklarında otomobil hızının yarıya indirirken motosiklet iki katına çıkarıyor ve otomobil bu karşılaşmadan 60 dakika sonra B kentine varıyor. Motosiklet bu karşılaşmadan kaç dakika sonra A kentine varır? A) 105 B) 120 C) 135 D) 150 E) 180 www.matematikkolay.net Çözüm: Otomobilin hızı 6V olsun. Motosikletin hızı 2V olur. A ile B arası mesade 8x olsun. 8x 8x x sürede karşılaşırlar. 6V 2V 8V v Bu karşılaşma anına kadar, x Otomobil 6V 6x yol gitmiştir. V x Motosiklet 2V V       6x 2x 2x yol gitmiştir. A X B Karşılaştık tan sonra Otomobilin hızı 3V, Motosikletin hızı 4V oluyor. Otomobil 2x’lik mesafeyi 60 dakikada alıyorsa; 2            x 60 3V  30 x 90V dir. Motosiklet 6x’lik mesafeyi ne kadar sürede alır, bulalım. 6x 6.90V 540V 135 dakika buluruz. 4V 4V 4V      140 www.matematikkolay.net A ve B şehirlerinden aynı anda birbirlerine doğru iki araç yola çıkıyor. A şehrinden hareket eden aracın hızı saatte 50 km dir. B şehrinden hareket eden aracın hızı saatte 70 km dir. A ve B şehirleri arasındaki mesafe 480 km dir. Buna göre, bu iki araç arasındaki mesafe kaç saat sonra ikinci kez 120 km olur? A) 4 B) 5 C) 6 D) 7 E) 8 Çözüm: İki araç karşılaşmadan önce aralarındaki mesade bir kere 120 km olur. 2.kez ise; karşılaşmadan sonra 120 km uzaklaşınca olur. Bu ana kadar toplam 480 120 600 km yol gitmiş olurlar. Hızları topl   amı 50 70 120 km / sa dir. Bu ana kadar, toplam 600 5 saat geçmiştir. 120 Cevap: 5     142 www.matematikkolay.net A ve B şehirlerinde bulunan iki hareketli aynı anda 45 km/ sa ve 35 km/ sa hızlarla karşılıklı olarak hareket ediyor. A ve B arasında durmadan tur atan bu iki aracın 3. karşılaşmaları 10 saat sonra olduğuna göre, A ve B arası kaç km dir? A) 160 B) 180 C) 200 D) 220 E) 240 www.matematikkolay.net   Çözüm: AB asası mesafe x olsun. Bu iki araç toplam x kadar mesafe gidince ilk karşılaşmaları gerçekleşir. Bu karşılaşmadan sonra iki araç B ve A ya varacak x kadar yol daha gidecekler , sonra da geri dönü   p tekrar karşılacaklar x kadar yol daha gidecekler Yani, ilk karşılaşmadan sonra 2x mesafe gittikten sonra 2.kez karşılaşırlar. 2.den sonra da 2x kadar yol gidince 3.kez karşılaşırlar. Toplam da x 2x 2x      5x yol gitmiş olurlar. 5x 10. 45 35 ise; 5x 10.80 5x 800 x 160 km buluruz.       143 A ve B şehirlerinden saatteki hızları sırasıyla 60 km ve 80 km olan iki araç birbirlerine doğru aynı anda hareket ediyorlar. Araçların hareket alanı A ve B noktaları arasıdır. www.matematikkolay.net Buna göre, sürekli hareket eden bu iki aracın 3. karşılaşmaları A şehrinden kaç km uzakta olur? A) 20 B) 30 C) 40 D) 50 E) 60 Çözüm: İlk karşılaşmaları için ikisi toplam AB arası kadar yol gider. İkinci karşılaşma için ikisi toplam AB kadar yol gidip, tekrar AB kadar yol dönünce karşılaşırlar. Yani 2 AB kadar yol giderler. Üçüncü karşılaşma için de 2 AB kadar yol giderler. Toplam 5 AB kadar yol gitmiş olacaklar. 5 AB 5.210 1050 km dir. Hızları toplamı 140 km dir. 1050 15 Geçen süre 7,5 saat 140 2 15 7,5 saatte A aracı 60 450 km gid 2          er. 210 km A’dan B’ye 210 km B’den A’ya Geriye 30 km kalır. 30 km A’dan uzakta karşılaşırlar. 151 www.matematikkolay.net A ve B noktalarından saatteki hızları 80 km/ sa ve 60 km/ sa olan iki araç aynı anda harekete başlayıp A ve B arasında durmaksızın tur yapıyorlar. İkinci kez C noktasında karşılaştıklarına göre, AB arası uzaklık kaç km olur? A) 450 B) 500 C) 600 D) 700 E) 850 Çözüm: www.matematikkolay.net 1 İkisi aynı anda yola çıkıp karşılaştıkları için hareket süreleri eşittir.Şimdi 2. buluşmaya kadar ayrı ayrı ne kadar yol almışlar onu bulalım. AB x olsun. ikisi de x km yol aldığında V hızlı B noktasına  2 2 V hızlı A noktasına gelir.Ve bir ker e karşılaşmışlardır. 2. karşılaşmaları dönüşte gerçekleşir.C noktasında karşılaştıklarına göre A noktasındaki V hızlı araç 200 km daha giderek toplam x 200 km gitmiş 1 olur. V hızlı olan ise x 200 km daha yol alarak 2x 200 km yol almış olur. Şimdi zamanlarını eşleyelim. 2x 200 80    4  x 200 60  3 6x 600 4x 800 2x 1400 x 700 km bulunur.         154 Bir kenarı 125 m olan kare şeklinde bir pistin A köşesinden dakikadaki hızları 3V ve 2V olan iki hareketli aynı anda zıt yönde harekete başlıyor ve E noktasında karşılaşıyorlar. www.matematikkolay.net Buna göre, EC kaç metredir? A) 285 B) 300 C) 305 D) 315 E) 325 Çözüm: 2V nin gittiği yol 250 x 3V nin gittiği yol 250 x Bu ikisi aynı sürede gerçekleştiğinden zamanı eşitleyen bir denklem kuralım. 250 x 2V      250 x 3V   250 x.3 250 x.2 750 3x 500 2x 750 500 5x 250 5x x 50 buluruz.           157