Soru Sor sayfası kullanılarak Faktöriyel konusu altında Faktöriyelli İfadelerin Sadeleştirilmesi ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
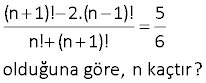
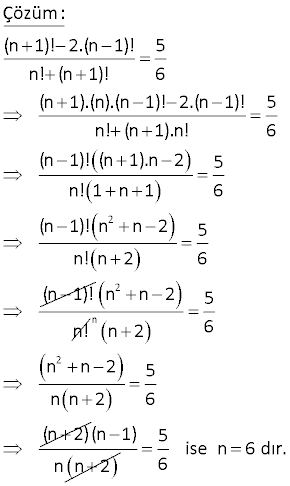
2.SORU


3.SORU
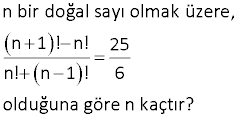
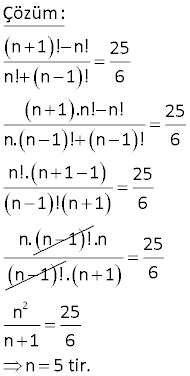
4.SORU


5.SORU


6.SORU


7.SORU


8.SORU
9.SORU

10.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
(n 1)! 2.(n 1)! 5 n! (n 1)! 6 olduğuna göre, n kaçtır? www.matematikkolay.net – 2 Çözüm: (n 1)! 2.(n 1)! 5 n! (n 1)! 6 (n 1).(n).(n 1)! 2.(n 1)! 5 n! (n 1).n! 6 (n 1)! (n 1).n 2 5 n! 1 n 1 6 (n 1)! n n 2 5 n! n 2 6 (n 1)! 2 n n 2 n! n 2 5 n 2 6 n n 2 5 n n 2 6 (n 2) (n 1) n n 2 5 ise n 6 dır. 6 3 www.matematikkolay.net n doğal sayı ve n 1 olmak üzere, n!. n 1 ! n 1 !. n 2 ! ifadesinin en sade şekli aşağıdakilerden hangisidir? n 1 n n A) B) C) n 2 n 2 n 1 1 D) n 1 ! E) n! Çözüm: n!.(n 1)! (n! ve (n 2)! ‘i birer adım açalım) (n 1)!.(n 2)! n. (n 1)!. (n1)! (n1)!. (n2). (n1)! (Sadeleştirelim) n buluruz. n 2 5 n bir doğal sayı olmak üzere, n 1 ! n! 25 n! n 1 ! 6 olduğuna göre n kaçtır? Çözüm: n 1 ! n! 25 n! n 1 ! 6 n 1 .n! n! 25 n. n 1 ! n 1 ! 6 n!. n 1 1 25 n 1 ! n 1 6 n. n 1 ! .n n1 ! 2 25 . n 1 6 n 25 n 1 6 n 5 tir. 16 10! 81.8! aşağıdakilerden hangisine eş ) ) ) ittir? A 6! B 7! C 7! 8! D) 9! E) 8! 9! 10.9! 9.9 9! Çözüm: 10! 81.8! ikisini aynı faktöriyel cinsinden yaz maya çalışalım. 10.9! 9.9.8! 10.9! 9.9! 9! parantezine alabiliriz. 9!.(10 9) 9!.1 9! buluruz. 11 11! ifadesinin eşiti (11 ni ! 10! bul 9 . ) z ! unu www.matematikkolay.net Çözüm: Faktöriyel ifadeleri 9! cinsinden yazalım. 11! 11.10.9! 11! 10! 9! 11.10.9! 10.9! 9! 11.10. 9! 9! 11.Eki (11.10 10 1) 110 10 1 11 .10 121 11 10 buluruz. 11 12 8! 9! 8! ifadesinin eşitini bulunuz. 7! 8! 9! 7! cinsinden 8! cinsinden yazalım. yazalım Çözüm: Faktöriyel ifadeleri 7! cinsinden yazalım. 8! 9! 8! 8.7! 9.8.7! 8! 7! 8! 9! 7! 8.7! 9.8! 7! (8 72) 7! 8! (1 8) 9. 8! 80 1 81 9 buluruz. 9 9 9 13 2 2 10! 9! 11! 10! 9! işleminin sonucu aşağıdakilerden hangisine eşittir? A) 8! B) 9! C) 10! D) 8.8! E) 8.9! 2 2 Çözüm: 10! 9! 10! 9! .(10! 9!) 11! 10! 9! 9!(10.11 10 1) 9! (10 1).9!(10 1) 9! 9!.9.11 9! bulunur. .99 99 18 (n 2)!.(3n 2)! 7 n!.(3n 3)! 3 olduğuna göre n kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 Çözüm: (n 2)!.(3n 2)! 7 n!.(3n 3)! 3 (n 2).(n 1).n! . (3n2)! n!.(3n 3). (3n2)! 7 3 (n 2). (n 1) 3. (n1) 7 3 n 2 7 n 5 bulunur. www.matematikkolay.net 28 www.matematikkolay.net (n 2)! 2(n 4)! (n 3)! (n 4)! ifadesinin eşiti nedir? n 4 A) n 3 B) n 1 C) n 3 n 3 D) n 4 E) n 2 (n 2)! 2(n 4)! (n 4)! e kadar genişletelim. (n 3)! (n 4)! (n 2)(n 3)(n 4)! 2(n 4)! (n 3)(n 4)! (n 4)! (n 4)! (n 2)(n 3) 2 (n 4)! n 3 1 (n 4)! 2 (n 5n 6) 2 (n 4)! 2 ( 4)( 1) n 4 n 5n 4 n 4 (n 4) (n 1) n 4 n1 buluruz. 30 n! 56 n 2 ! olduğuna göre, n kaçtır? A) 4 B) 5 C) 6 D) 7 E) 8 www.matematikkolay.net Çözüm: n! 56 (n 2)! n.(n 1). (n 2)! (n2)! 56 n.(n 1) 56 8.7 56 olduğundan n 8 dir.

