Soru Sor sayfası kullanılarak Faktöriyel konusu altında Faktöriyel İçinde Çarpan Sayısı Arama ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

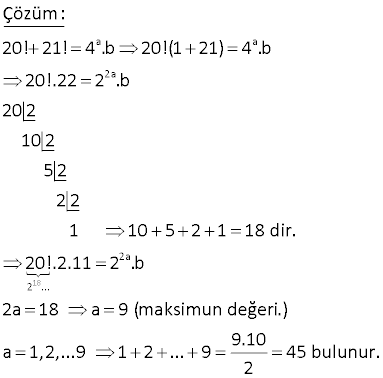
4.SORU
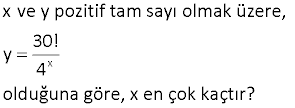

5.SORU


6.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
www.matematikkolay.net n n bir doğal sayı olmak üzere, 74! 14 ifadesi bir tam sayı olduğuna göre, n’nin alabileceği kaç farklı değer vardır? A) 10 B) 11 C) 12 D) 13 E) 14 Çözüm: 14 2 ve 7 asal sayılarının çarpımıdır. 7 daha büyük bir asal sayı olduğu için 74!’in içinde daha azdır. O yüzden 74!’in içinde kaç tane 7 vardır, hesaplayalım. 74 7 10 7 11 1 Bölümleri toplayalım, 10 1 11 dir. En fazla 7 olduğunda 74’ü tam bölebilir. Bu sebeple n en fazla 11 olabilir. Alabileceği tam sayı değerleri; 0,1,….,10,11 12 tane Cevap: C şıkkı 8 www.matematikkolay.net x x ve y birer sayma sayısı olmak üzere, 97! 36 .y eşitliğinde y sayısı 3’ün katı olan bir doğal sayı olduğuna göre, x’in alabileceği en büyük değer kaçtır? A) 22 B) 23 C) 24 D) 25 E) 26 2 2 x 2 2 x 2x 2x 2x 2x 1 Çözüm: 36’yı asal çarpanlarına ayırarak yazalım. 36 4.9 2 .3 dir. y sayısı 3’ün katı bir sayı ise, x ‘in en büyük olması için y ‘ ye 3 diyelim. Buna göre; 97! 36 .3 97! (2 .3 ) .3 97! 2 .3 .3 97! 2 .3 3 daha büyük bir asal sayı olduğu için 97!’in içinde kaç tane 3 vardır, hesaplayalım. 97 3 32 3 10 3 3 3 1 Bölümlerin toplamı 1 3 10 32 46 buluruz. yani 2x 1 en fazla 46 olabilir. 2x 1 46 2x 45 x bir sayma sayısı olduğundan en fazla 22 olabilir. www.matematikkolay.net 9 a a ve b pozitif tam sayılardır. 20!+21!=4 .b olduğuna göre, a’nın alabileceği farklı değerler toplamı kaçtır? A) 36 B) 38 C) 40 D) 42 E) 45 www.matematikkolay.net 18 a a 2a 2a 2 … Çözüm: 20! 21! 4 .b 20!(1 21) 4 .b 20!.22 2 .b 20 2 10 2 5 2 2 2 1 10 5 2 1 18 dir. 20!.2.11 2 .b 2a 18 a 9 (maksimun değeri.) 09.Eki a 1,2,…9 1 2 … 9 45 2 bulunur. 17 x x ve y pozitif tam sayı olmak üzere, 30! y 4 olduğuna göre, x en çok kaçtır? www.matematikkolay.net Çözüm: 30’un için de “2” asal çarpanının kaç tane olduğunu bulalım. 30 2 15 2 7 2 3 2 1 Bölümleri toplarsak; 137 15 2 x 2x 6 dır. 4 2 tir. 2x 26 olabiliyorsa; x 13 olur (en çok) 22 www.matematikkolay.net n a ve n birer doğal sayı olmak üzere, 6! 3 .a olduğuna göre, n’nin alabileceği en büyük değer kaçtır? A) 0 B) 1 C) 2 D) 3 E) 4 n Çözüm: 6! 3 .a n en fazla 6!’in içindeki 3 çarpanı sayısını alabilir. 6 3 6 2 0 n’nin en büyük değeri 2 bulunur. 24 n A çift sayı olmak üzere, 33! A olduğuna göre, n’nin alabileceği değerler 8 toplamı kaçtır? A) 30 B) 35 C) 50 D) 55 E) 60 www.matematikkolay.net n 3n Çözüm: 8 2 dir. 33! içinde kaç tane 2 var, bulalım. 33 2 16 2 8 2 4 2 2 2 1 Bölümlerin toplam 31 30 3n 30 ı 1 2 4 8 16 31 dir. Buna göre 3n en fazla 31 olurdu. Ancak, A çift sayı ise; 2 değil de, 2 olmalı. Bu şekilde A, her durumda 2’nin katı olmaya devam eder. 2 2 n 10 dur. (en fazla) Buna gör e; n’in alacağı değerler toplamı 10.Kas 0 1 2 … 10 55 buluruz. 2 26

