 Bu bölümde Üslü Sayılar Tanım ve Dört İşlem konusu ile ilgili 28 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Bu bölümde Üslü Sayılar Tanım ve Dört İşlem konusu ile ilgili 28 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Konu Anlatımı için Tıkla
Üslü Sayılar Tanım ve Dört İşlem Çözümlü Soruları pdf indir
Kitap Formatında Görmek için Tıkla
ÜSLÜ SAYILAR TANIM VE DÖRT İŞLEM ÇÖZÜMLÜ SORULARI
SORU: 1)
![]() ifadesinin üslü sayılar biçiminde yazılışı aşağıdakilerden hangisidir?
ifadesinin üslü sayılar biçiminde yazılışı aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
n tane a’nın çarpımı ![]() şeklinde ifade edilir. Yani;
şeklinde ifade edilir. Yani; ![]() dir. Buna göre
dir. Buna göre ![]() olarak buluruz. Doğru Cevap: B şıkkı
olarak buluruz. Doğru Cevap: B şıkkı
SORU: 2)
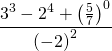
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Not : ![]()
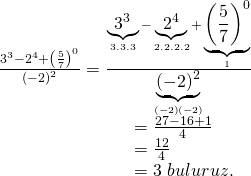
Doğru Cevap : E şıkkı
SORU: 3)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Negatif bir sayının çift kuvvetleri pozitif olup tek kuvvetleri ise negatiftir. Bu soruda ayrıca parantezlere dikkat edilmesi gerekiyor. Mesela ![]() ifadesinde 2’nin 2’nci kuvveti alınıp eksi ile çarpılıyor(yani ( – 2)’nin 2. kuvveti alınmıyor). Buna göre;
ifadesinde 2’nin 2’nci kuvveti alınıp eksi ile çarpılıyor(yani ( – 2)’nin 2. kuvveti alınmıyor). Buna göre;
![]()
![]()
Doğru Cevap : D şıkkı
SORU: 4)
n bir doğal sayı olmak üzere,
![]()
![]()
ÇÖZÜM:
Negatif bir sayının çift kuvvetleri pozitif olup tek kuvvetleri ise negatiftir. Bu soruda ayrıca parantezlere dikkat edilmesi gerekiyor. Mesela ![]() ifadesinde 1’in 2n’nci kuvveti alınıp eksi ile çarpılıyor(yani (-1)’in 2n. kuvveti alınmıyor). Buna göre;
ifadesinde 1’in 2n’nci kuvveti alınıp eksi ile çarpılıyor(yani (-1)’in 2n. kuvveti alınmıyor). Buna göre;
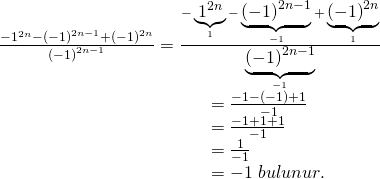
Doğru Cevap : D şıkkı
SORU: 5)
![]() ve
ve ![]() olmak üzere,
olmak üzere,
![]()
ifadesinin değeri kaçtır?
A) 8 B) 9 C) 10 D) 11 E) 12
ÇÖZÜM:
![]() değerlerini yerine yazarsak;
değerlerini yerine yazarsak;
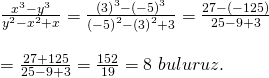
Doğru Cevap : A şıkkı
SORU: 6)
![]() olmak üzere,
olmak üzere,
![]()
ifadesinin değeri aşağıdakilerden hangisidir?
A) 30 B) 32 C) 45 D) 56 E) 67
ÇÖZÜM:
![]() değerlerini yerine yazarsak
değerlerini yerine yazarsak
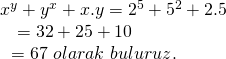
Doğru Cevap: E şıkkı
SORU: 7)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Bir sayının negatif üssü, onun bölme işlemine göre tersini ifade eder.
![]()
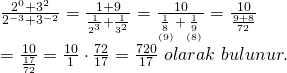
Doğru Cevap : C şıkkı
SORU: 8)
![]()
işleminin sonucu kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6
ÇÖZÜM:
Bir sayının negatif üssü onun bölme işlemine 1 tersini ifade eder.
![]()
Buna göre;
![]()
Doğru Cevap : B şıkkı
SORU: 9)
![]() işleminin sonucu kaçtır?
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Üslü sayılarda toplama ya da çıkarma işlemi yapabilmek için üslü sayıların tabanları ve üslerinin aynı olması gerekir. ![]() ifadesindeki üslü ifadeler aynı olacak şekilde düzenleme yapalım.
ifadesindeki üslü ifadeler aynı olacak şekilde düzenleme yapalım.
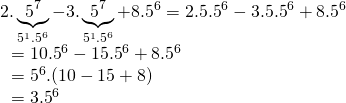
Doğru Cevap: D şıkkı
SORU: 10)
![]()
işleminin sonucu kaçtır?
A) 3 B) 6 C) 9 D) 18 E) 27
ÇÖZÜM:
Tabanları aynı olan iki üslü sayı çarpılırsa sadece üsler toplanır.
![]() bulunur.
bulunur.
Doğru Cevap: C şıkkı
SORU: 11)
![]() işleminin sonucu kaçtır?
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Not :Üsleri aynı olan iki üslü sayı çarpılırsa tabanlar çarpılır.
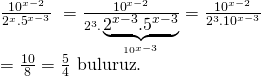
Doğru Cevap : E şıkkı
SORU: 12)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
![]()
Doğru Cevap : A şıkkı
SORU: 13)
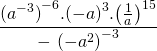
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Not : Üslü sayının kuvveti alınıyorsa üsler çarpılır.
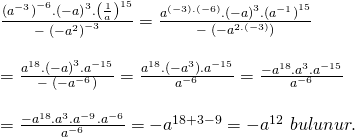
Doğru Cevap : D şıkkı
SORU: 14)
![]()
çarpımının sonucu kaç basamaklıdır?
A) 8 B) 9 C) 10 D) 11 E) 12
ÇÖZÜM:
![]() çarpımının kaç basamaklı olduğunu bulmak için sayıyı 10’un kuvvetleri şeklinde ifade etmeliyiz. İlk önce sayıyı asal çarpanlarına tamamen ayıralım daha sonra; 2 ve 5 asal çarpanlarını kullanarak 10’un kuvveti şeklinde ifade edelim.
çarpımının kaç basamaklı olduğunu bulmak için sayıyı 10’un kuvvetleri şeklinde ifade etmeliyiz. İlk önce sayıyı asal çarpanlarına tamamen ayıralım daha sonra; 2 ve 5 asal çarpanlarını kullanarak 10’un kuvveti şeklinde ifade edelim.
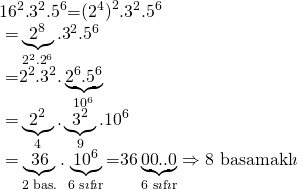
Doğru Cevap: A şıkkı
SORU: 15)
![]()
işleminin sonucu aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
Not : Üslü sayılarda bölme işlemi yaparken tabanlar aynı ise sadece üsler çıkarılır. Buna göre;
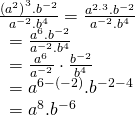
Doğru Cevap: E şıkkı
SORU: 16)
![]() sayısının yarısı kaçtır?
sayısının yarısı kaçtır?
![]()
ÇÖZÜM:
Bir sayının yarısı demek onu 2’ye bölmektir. Yani soruda bizden ![]() nin cevabı isteniyor. Buna göre
nin cevabı isteniyor. Buna göre
![]()
Doğru Cevap: D şıkkı
SORU: 17)
![]()
işleminin sonucu kaçtır?
A) 4 B) 5 C) 6 D) 7 E) 8
ÇÖZÜM:
Üsleri aynı olan sayıları bölerken sadece tabanları böleriz. Buna göre;
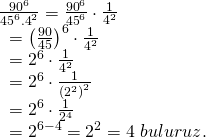
Doğru Cevap : A şıkkı
SORU: 18)
![]()
ifadesinin en sade şekli aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
Üsleri aynı olan sayıları bölerken, sadece tabanlar arası bölme işlemini gerçekleştirebiliriz. Buna göre;
![]()
Burada iki kare farkı formülünden yararlanalım. ![]()
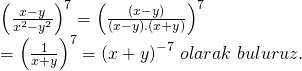
Doğru Cevap : E şıkkı
SORU: 19)
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Tabanları aynı olan üslü sayılar çarpılırken üsler toplanır. Buna göre;
![]()
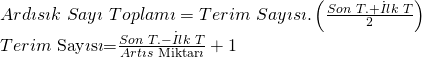
Buna göre;
![]()
Doğru Cevap: C şıkkı
SORU: 20)
![]() olduğuna göre,
olduğuna göre,
![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
Bölme işlemini yaparsak;

Doğru Cevap : C şıkkı
SORU: 21)
![]()
ifadenin en sade şekli aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
Bölme işlemindeki tüm sayıları 3’ün kuvveti şeklinde yazalım;
![]()
üssü en küçük olan sayının ortak çarpanı şeklinde yazalım;
![]()
olarak buluruz.
Doğru Cevap: A şıkkı
SORU: 22)
![]()
işleminin sonucu kaçtır?
A) 0 B) 1 C) 2 D) 3 E) 4
ÇÖZÜM:
![]() yerine
yerine ![]() ifadesini yerleştirerek başlayalım;
ifadesini yerleştirerek başlayalım;
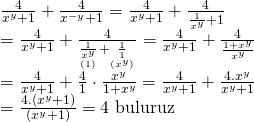
Doğru Cevap : E şıkkı
SORU: 23)
![]() olduğuna göre,
olduğuna göre, ![]() ifadesinin y cinsinden eşiti aşağıdakilerden hangisidir?
ifadesinin y cinsinden eşiti aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
![]()
![]() ifadesini
ifadesini ![]() şeklinde ifade edelim.
şeklinde ifade edelim.
![]()
Doğru Cevap : B şıkkı
SORU: 24)
![]()
olduğuna göre, ![]()
işleminin sonucu kaçtır?
![]()
ÇÖZÜM:
![]()
![]() ifadesini
ifadesini ![]() şeklinde ifade edelim.
şeklinde ifade edelim.
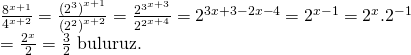
Doğru Cevap : D şıkkı
SORU: 25)
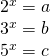
olduğuna göre, ![]() ifadesinin a,b ve c cinsinden eşiti aşağıdakilerden hangisidir?
ifadesinin a,b ve c cinsinden eşiti aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
![]() ifadesini çarpanları 2 ve 5 olacak şekilde ifade edelim;
ifadesini çarpanları 2 ve 5 olacak şekilde ifade edelim;
![]()
Doğru Cevap: E şıkkı
SORU: 26)
![]()
olduğuna göre, ![]() ifadesinin a ve b cinsinden eşiti aşağıdakilerden hangisidir?
ifadesinin a ve b cinsinden eşiti aşağıdakilerden hangisidir?
![]()
ÇÖZÜM:
![]()
Buna göre; ![]() ifadesini 8 ve 9 çarpanları şeklinde ifade edelim;
ifadesini 8 ve 9 çarpanları şeklinde ifade edelim;
![]()
Doğru Cevap : C şıkkı
SORU: 27)
![]()
işleminin sonucu aşağıdakilerden hangisidir?
A) 2 B) 4 C) 6 D) 8 E) 16
ÇÖZÜM:
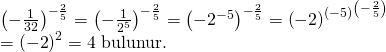
Doğru Cevap: B şıkkı
SORU: 28)
![]() sayısı
sayısı ![]() sayısının kaç katıdır?
sayısının kaç katıdır?
A) 2 B) 3 C) 6 D) 9 E) 27
ÇÖZÜM:
Soruda bizden ![]() in kaç olduğu isteniyor. İki 9 ifadeyi de 3’ün kuvvetleri şeklinde yazarsak;
in kaç olduğu isteniyor. İki 9 ifadeyi de 3’ün kuvvetleri şeklinde yazarsak;
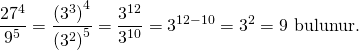
Doğru Cevap: D şıkkı
Kitap Formatında Görmek için Tıkla

