Hareket Problemleri (Latex Formatı)

Bu bölümde Hareket Problemleri ile ilgili 23 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…


SORULAR

SORU 1


Bir otomobil 120 km/sa hızla 6 saatte aldığı yolu 90 km/sa hızla kaç saatte alır?

A) 6 B) 7 C) 8 D) 9 E) 10

Doğru Cevap Çözüm için Tıklayınız

SORU 2

A şehrinden B şehrine 10 saatte giden bir araç, geri dönerken hızını 30 km/sa artırarak 7 saatte A şehrine varmıştır. Buna göre A şehri ile B şehri arasındaki mesafe kaç km dir?

A) 600 B) 700 C) 750 D) 800 E) 850

Doğru Cevap Çözüm için Tıklayınız

SORU 3

A şehrinden aynı anda yola çıkan 2 aracın hızları 80 km/sa ve 50 km/sa olup B şehrine varacaklardır. Hızlı olan araç B şehrine 6 saat önce vardığına göre A şehri ile B şehri arasındaki uzaklık kaç km dir?

A) 600 B) 700 C) 800 D) 900 E) 1000

Doğru Cevap Çözüm için Tıklayınız

SORU 4

Bir araç iki şehir arasında yol gidip gelmiştir. Giderken 72 km/sa hız kullanan bu araç hiç beklemeden dönüş yapmıştır. Dönerken kullanılan hız 60 km/sa olup toplam yolculuk 11 saat sürmüştür. Buna göre iki şehir arasındaki mesafe kaç km dir?

A) 200 B) 220 C) 250 D) 300 E) 360

Doğru Cevap Çözüm için Tıklayınız

SORU 5

Bir araç 300 km lik bir yolun bir kısmını 50 km/sa hızla, bir kısmını ise 30 km/sa hızla gidip; bu yolculuğu 8 saatte tamamlıyor. Buna göre bu araç 50 km/sa hızla kaç km yol gitmiştir?

A) 100 B) 120 C) 140 D) 150 E) 180

Doğru Cevap Çözüm için Tıklayınız

Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU 6

Hızları 90 km/sa ve 60 km/sa olan iki araç 450 km lik bir yolu alacaklardır. Hızlı olan araç yolu bitirdiğinde yavaş olan aracın daha kaç km yolu vardır?

A) 150 B) 200 C) 250 D) 300 E) 350

Doğru Cevap Çözüm için Tıklayınız

SORU 7

Hızı bilinmeyen bir araç ile hızı 60 km/sa olan bir araç aynı noktadan ters yönlerde hareket etmeye başlıyor. 5 saat sonra aralarındaki mesafe 700 km olduğuna göre hızı bilinmeyen aracın hızı kaç km/sa dır?

A) 80 B) 100 C) 120 D) 180 E) 200

Doğru Cevap Çözüm için Tıklayınız

SORU 8

Fatih, gideceği bir yolun yarısını yürüyerek gittikten sonra diğer yarısını hızını 2 katına çıkararak koşarak tamamlamıştır. Tüm yolu 2 saatte tamamlayan Fatih, tüm yolu yürüyerek gitseydi kaç saatte yolculuğu tamamlardı?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }2,5\text{ }} & {B)\text{ }\frac{7}{3}} & {C)\text{ }\frac{8}{3}} & {D)\text{ 3}} & {E)\text{ 3}\text{,5}} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 9

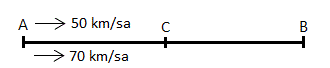
hrkt_prb_s17rl

Hızları 50 km/sa ve 70km/sa olan iki araç aynı anda A şehrinden B şehrine gitmek üzere doğru yola çıkıyor. B’ye erken varan araç, hiç beklemeden geri döndüğünde C şehrinde yavaş olan araçla karşılaşıyor. İki araç yola çıktıktan 4 saat sonra
karşılaştıklarına göre, A ile B şehirleri arası mesafe kaç km dir?

A) 160 B) 180 C) 200 D) 220 E) 240

Doğru Cevap Çözüm için Tıklayınız

SORU 10

Aralarındaki uzaklık 1600 km olan iki şehirden karşılıklı olarak birbirlerine doğru hareket eden iki araç 8 saat sonra karşılaşıyorlar. Araçlardan birinin hızı 70 km/sa olduğuna göre, diğer aracın hızı kaç km/sa dır?

A) 100 B) 110 C) 120 D) 130 E) 140

Doğru Cevap Çözüm için Tıklayınız

SORU 11

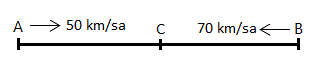
hrkt_prb_s21rl

Hızları 50 km/sa ve 70 km/sa olan iki araç karşılıklı olarak birbirlerine doğru hareket ediyorlar. C noktasında karşılaşan bu araçlardan hızlı olan araç 5 saat sonra A noktasına ulaşıyor. Buna göre A ve B arası mesafe kaç km dir?

A) 800 B) 840 C) 850 D) 900 E) 960

Doğru Cevap Çözüm için Tıklayınız

SORU 12

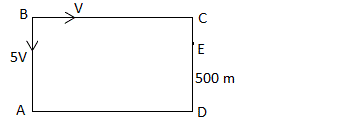
hrkt_prb_s23rl

Hızları verilen iki tavşan dikdörtgen biçimindeki bir tarlanın çevresinde A noktasından ters yönlerde hareket ediyolar. E noktasında bu tavşanlar karşılaştığına göre tarlanın çevresi kaç m dir?

A) 1200 B) 1300 C) 1500 D) 1800 E) 2000

Doğru Cevap Çözüm için Tıklayınız

SORU 13

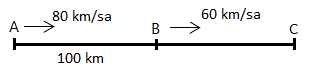
hrkt_prb_s25rl

Aralarında 100 km uzaklık bulunan iki araçtan geride olan aracın hızı 80 km/sa, öndekinin ise 60 km/sa dır. Buna göre, arkadaki araç kaç saat sonra öndeki aracı yakalar?

A) 3 B) 4 C) 5 D) 6 E) 7

Doğru Cevap Çözüm için Tıklayınız

SORU 14

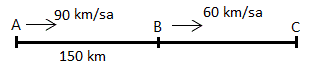
hrkt_prb_s27rl

Şekildeki gibi A noktasından 90 km/sa hızla yola çıkan araç, 150 km ileride 60 km/sa hızla hareket eden aracı C noktasında yakalıyor. Buna göre A ile C arası kaç km dir?

A) 350 B) 450 C) 500 D) 600 E) 650

Doğru Cevap Çözüm için Tıklayınız

SORU 15

Aralarında 360 km mesafe bulunan şehirlerden hareket eden iki araç, birbirlerine doğru hareket ederlerse 2 saatte karşılaşıyorlar. Şayet, bu iki araç aynı yönde hareket ederse hızlı olan araç yavaş olan aracı 18 saatte yakalıyor. Buna göre yavaş olan aracın hızı kaç km/sa dır?

A) 50 B) 60 C) 70 D) 80 E) 100

Doğru Cevap Çözüm için Tıklayınız

SORU 16

Durgun sudaki hızı 25 km/sa olan bir deniz motoru, akıntı hızı 5 km/sa olan bir denizde kıyıdan akıntı yönünde gidecek şekilde hareket ediyor ve hiç durmadan başladığı yere geri dönüyor. Tüm yolculuğu 5 saat süren bu deniz motoru, denizde kaç km yol gitmiştir?

A) 60 B) 80 C) 90 D) 100 E) 120

Doğru Cevap Çözüm için Tıklayınız

SORU 17

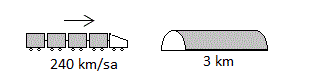
hrkt_prb_s33rl

240 km/ sa hızla giden bir yüksek hızlı tren 3 km ‘lik bir tüneli 48 saniyede geçtiğine göre bu trenin boyu kaç metredir?

A) 200 B) 250 C) 300 D) 350 E) 400

Doğru Cevap Çözüm için Tıklayınız

SORU 18

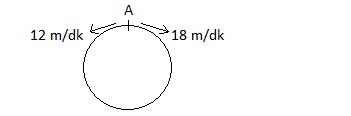
hrkt_prb_s35rl
Çevresi 360 metre olan dairesel bir pistin A noktasından hızları 12 m/dk ve 18 m/dk olan iki araç zıt yönde harekete başlıyorlar. Bu araçlar ilk defa kaç dk sonra karşılaşırlar?

A) 9 B) 10 C) 11 D) 12 E) 15

Doğru Cevap Çözüm için Tıklayınız

SORU 19

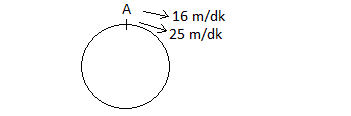
hrkt_prb_s37rl

Çevresi 270 metre olan dairesel bir pistin A noktasından hızları 16 m/dk ve 25 m/dk olan iki araç aynı yönde harekete başlıyorlar. Buna göre hızlı olan araç yavaş olan aracı kaç dakika sonra yakalar?

A) 30 B) 35 C) 40 D) 45 E) 50

Doğru Cevap Çözüm için Tıklayınız

SORU 20

Bir araç 750 km lik yolun 300 km sini 60 km/sa hızla, kalan 450 km lik kısmını ise 45 km/sa hızla gidiyor. Buna göre bu aracın ortalama hızı kaç km/sa dır?

A) 30 B) 35 C) 40 D) 45 E) 50

Doğru Cevap Çözüm için Tıklayınız

SORU 21

Bir araç 40 km/sa hızla gittiği yolu, 60 km/sa hızla geri dönmüştür. Buna göre, bu aracın ortalama hızı kaç km/sa dır?

A) 42 B) 45 C) 48 D) 50 E) 52

Doğru Cevap Çözüm için Tıklayınız

SORU 22

Boyları eşit olan iki mumdan biri 4 saatte, diğeri ise 5 saatte erimektedir. Aynı anda ikisi erimeye başlarsa kaç saat sonra birinin boyu diğerinin yarısı olur?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }3\text{ }} & {B)\text{ }\frac{{10}}{3}} & {C)\text{ }4} & {D)\text{ }\frac{{13}}{3}} & {E)\text{ }\frac{{14}}{3}} \end{array}

Doğru Cevap Çözüm için Tıklayınız

SORU 23

Saat 13:20 te akrep ile yelkovan arasındaki açı kaç derecedir?

A) 50 B) 60 C) 70 D) 80 E) 90

Doğru Cevap Çözüm için Tıklayınız
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

SORU ÇÖZÜMLERİ

ÇÖZÜM 23

Akrep ile yelkovan arasındaki açı şu formülle bulunur :\displaystyle Ac\imath =\frac{{\left| {11.dakika-60.saat} \right|}}{2}Soruda saat 13:20 olduğuna göre bunu formülde ilgili yerlere yerleştirelim,
(Saat 13, 12’lik bir saatte 1’e denktir.)\displaystyle Ac\imath =\frac{{\left| {11.20-60.1} \right|}}{2}=\frac{{\left| {220-60} \right|}}{2}=\frac{{160}}{2}={{80}^{0}}
Doğru Cevap : D şıkkı

Soruyu Gör
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

ÇÖZÜM 22

Mumların boyunu hız cinsinden ifade edersek bu soruyu daha kolay çözeriz. Bir mum 4 saatte diğer mum 5 saatte eridiğine göre bu sayıların ortak katı olan 20 ile mumların boyunu ifade edelim. Buna göre;

Mumların Boyu 20V olsun.
1.mumun erime hızı : 5V
2.mumun erime hızı: 4V olur.

t süre sonra;
\displaystyle \frac{{1.mumun\text{ }boyu}}{{2.mumun\text{ }boyu}}=\frac{{20V-5V.t}}{{20V-4V.t}}=\frac{1}{2}
\displaystyle 40V-10Vt=20V-4Vt
\displaystyle 20V=6Vt
\displaystyle t=\frac{{20}}{6}=\frac{{10}}{3} saat bulunur.
Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 21

Yola x dersek;
40 km/ sa ile geçen süre: \displaystyle {{t}_{1}}=\frac{x}{{40}}
60 km/ sa ile geçen süre: \displaystyle {{t}_{2}}=\frac{x}{{60}}
O halde;
Toplam Yol 2x
\displaystyle {{V}_{{ort}}}=\frac{{Toplam\text{ }Yol}}{{Toplam\text{ }Zaman}}=\frac{{2x}}{{\frac{x}{{40}}+\frac{x}{{60}}}}
\displaystyle =\frac{{2x}}{{\underset{{(3)}}{\mathop{{\frac{x}{{40}}}}}\,+\underset{{(2)}}{\mathop{{\frac{x}{{60}}}}}\,}}=\frac{{2x}}{{\frac{{3x+2x}}{{120}}}}
\displaystyle =\frac{{2x}}{1}\cdot \frac{{120}}{{5x}}
\displaystyle =\frac{{240}}{5}
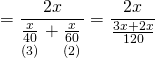
\displaystyle =48\text{ km/sa} buluruz.
Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 20

Ortalama hız, toplam yolun toplam zamana bölünmesi ile bulunur. Soruda toplam yolu biliyoruz ama zamanı bilmiyoruz. Onun için zamanları hesaplayalım
60 km/ sa ile geçen süre: \displaystyle {{t}_{1}}=\frac{{300}}{{60}}=5\text{ }saat
45 km/ sa ile geçen süre: \displaystyle {{t}_{2}}=\frac{{450}}{{45}}=10\text{ }saat
O halde;
\displaystyle {{V}_{{ort}}}=\frac{{Toplam\text{ }Yol}}{{Toplam\text{ }Zaman}}=\frac{{750}}{{15}}=50\text{ }km/sa\text{ } buluruz.
Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 19

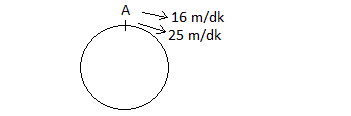
hrkt_prb_s38rl
Araçlar aynı yönde hareket ettikleri için hızları farkı kadar birbirlerine yaklaşırlar.
Hızlı olan aracın kapatacağı yol farkı ise pistin çevresi kadardır. Buna göre;
\displaystyle x=({{V}_{1}}-{{V}_{2}}).t
\displaystyle 270=(25-16).t
\displaystyle 270=9.t
\displaystyle t=30\text{ }dk buluruz.
Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 18

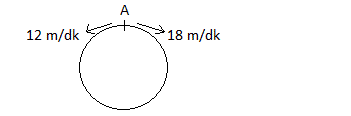
hrkt_prb_s36rl
Araçlar zıt yönde hareket ettikleri için hızları toplamı kadar birbirlerine yaklaşırlar. Buna göre;
\displaystyle x=({{V}_{1}}+{{V}_{2}}).t
\displaystyle 360=(12+18).t
\displaystyle 360=30.t
\displaystyle t=12 dk buluruz.
Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 17

hrkt_prb_s34rl
Tren köprüden tamamen çıkana kadar hem köprünün uzunluğu hem de kendi uzunluğu kadar yol alır. Ayrıca soruda süre sn cinsinden verilmiş.Bunu saate dönüştürelim,
\displaystyle 48\text{ }saniye=48.\frac{1}{{60}}.\frac{1}{{60}}=\frac{1}{{75}}saat
Buna göre;
Trenin uzunluğu + Köprü = Trenin Hızı x Süre
\displaystyle x+3=240.\frac{1}{{75}}
\displaystyle x+3=3,2
\displaystyle x=0,2\text{ }km=200\text{ }metre
Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 16

Akıntı yönünde hız, normal hızla akıntı hızının toplamına eşittir \displaystyle =\text{ }25+5=30 km / sa
Akıntıya karşı hız ise normal hızdan akıntı hızının çıkarılması ile bulunur \displaystyle =\text{ }25-5=20 km / sa
Deniz motorunun akıntı yönünde gidiş süresine t saat dersek, dönüş süresine \displaystyle 5-t diyebiliriz.
Gidilen yol ile Dönülen yol eşit olduğu için;
\displaystyle 30.t=20.(5-t)
\displaystyle 30t=100-20t
\displaystyle 50t=100
\displaystyle t=2\text{ }saat
\displaystyle Toplam\text{ }gidilen\text{ }yol\text{ }=30.t+20.(5-t)
\displaystyle =30.2+20.(5-2)
\displaystyle =60+60=120 km bulunur.
Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 15

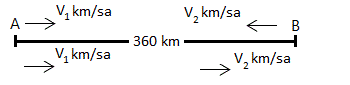
hrkt_prb_s30rl

İki araç birbirlerine doğru hareket ettiğinde hızları toplamına göre işlem yapılır. Buna göre;
\displaystyle x=({{V}_{1}}+{{V}_{2}}).t\text{ }\Rightarrow \text{ }360=({{V}_{1}}+{{V}_{2}}).2
\displaystyle {{V}_{1}}+{{V}_{2}}=180
İki araç birbirlerini yakalamaya uğraşıyorsa hızları farkına göre işlem yapılır.
\displaystyle x=({{V}_{1}}-{{V}_{2}}).t\text{ }\Rightarrow \text{ }360=({{V}_{1}}-{{V}_{2}}).18
\displaystyle {{V}_{1}}-{{V}_{2}}=20
Elde ettiğimiz bu iki denklemi çözelim,
\displaystyle {{V}_{1}}+{{V}_{2}}=180
\displaystyle \underline{{\text{ }+\text{ }{{V}_{1}}-{{V}_{2}}=20\text{ }}}
\displaystyle 2{{V}_{1}}=200\text{ }\Rightarrow \text{ }{{V}_{1}}=100  100 km/ sa bulunur.
Buna göre \displaystyle {{V}_{2}}=180-100=80 km/ sa bulunur.
Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 14

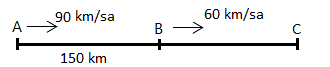
hrkt_prb_s28rl

İki araç aradaki mesafeyi, hızları farkı miktarınca kapatabilir. Buna göre;
Aradaki mesafe = Hız farkı x Süre
\displaystyle 150=(90-60).t
\displaystyle 150=30.t
\displaystyle t=5 saat buluruz.

A’dan hareket eden araç 5 saatte, öndeki aracı yakaladığı gibi; C noktasına ulaşması da 5 saat sürmüştür.
\displaystyle \left| {AC} \right|=90.5=450 km buluruz.
Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 13

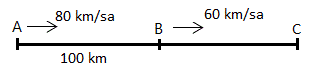
İki araç aradaki mesafeyi, hızları farkı miktarınca kapatabilir. Buna göre;
Aradaki mesafe = Hız farkı x Süre
\displaystyle 100=(80-60).t
\displaystyle 100=20.t
\displaystyle t=5 saat buluruz.
Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 12

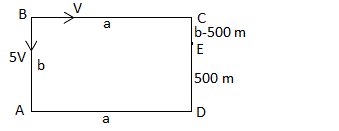
Dikdörtgenin uzun kenarına a, kısa kenarına da b diyelim. Buna göre;

hızı V olan tavşanın gittiği yol = a + b = 500
hızı 5V olan tavşanın gittiği yol = b + a + 500

İkisi aynı anda karşılaştıklarına göre harcanan zaman birbirine eşittir. Biz de bu süreleri eşitleyerek soruyu çözelim,
\displaystyle t=\frac{{{{x}_{1}}}}{{{{v}_{1}}}}=\frac{{{{x}_{2}}}}{{{{v}_{2}}}}\text{ }\Rightarrow \text{ }\frac{{a+b-500}}{V}=\frac{{a+b+500}}{{5V}}
\displaystyle \frac{{a+b-500}}{1}=\frac{{a+b+500}}{5}
\displaystyle 5a+5b-2500=a+b+500
\displaystyle 4a+4b=500+2500
\displaystyle 4(a+b)=3000
\displaystyle a+b=750\text{ }m
Dikdörtgenin çevresi\displaystyle =2(a+b)=2.750=1500 m dir.
Doğru Cevap: C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 11

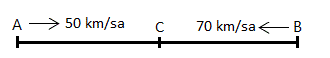
hrkt_prb_s22rl

Hızı 70 km / sa olan araç A ile C arasını 5 saatte tamamladıysa;
\displaystyle \left| {AC} \right|=70.5=350 km dir.
A ile C arasını yavaş olan aracın kaç saatte tamamladığını bulalım,
\displaystyle t=\frac{x}{V}=\frac{{350}}{{50}}=7 saat
Aynı anda bu 7 saatte hızlı olan araç B ile C arasını tamamlamıştır. Buna göre;
\displaystyle \left| {BC} \right|=70.7=490 km dir.
Buna göre mesafeleri toplayalım,
\displaystyle \left| {AB} \right|=\left| {AC} \right|+\left| {BC} \right|=350+490=840 km buluruz.
Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 10

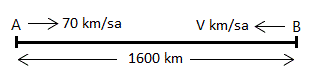
hrkt_prb_s20rl

Karşılıklı birbirlerine doğru hareket eden araçlar hızları toplamınca birbirlerine yaklaşırlar. Buna göre;
\displaystyle x=({{V}_{1}}+{{V}_{2}}).t
\displaystyle 1600=(70+V).8
\displaystyle 200=70+V
\displaystyle V=130\text{ }km/sa bulunur.
Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 9

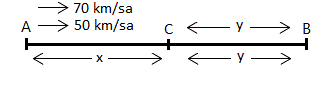
hrkt_prb_s18rl

A ile C şehirleri arası mesafeye x, B ile C şehirleri arası mesafeye y diyelim. Buna göre;
Hızı 50 km / sa olan 4 saatte araç x km gitmiştir.
\displaystyle x=50.4=200\text{ }km dir.
Hızı 70 km / sa olan araç 4 saatte \displaystyle x+y+y gitmiştir.
\displaystyle x+2y=70.4
\displaystyle x+2y=280
\displaystyle 200+2y=280
\displaystyle 2y=80
\displaystyle y=40 bulunur.

A ile B şehrinin arası \displaystyle x+y idi. Buna göre;
\displaystyle x+y=200+40=240 km dir.
Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 8

Yürürken yapılan hıza V, geçen süreye de t dersek, koşu hızı 2V, geçen süre de 2 t saattir.
Yola x dersek,
yolun yarısı \displaystyle =\frac{x}{2}=V.t (yürürken)
yolun yarısı \displaystyle =\frac{x}{2}=2V.(2-t) (koşarken)
Buna göre bu iki denklemi birbirine eşitleyelim,
\displaystyle V.t=2V.(2-t)
\displaystyle Vt=4V-2Vt
\displaystyle 3Vt=4V
\displaystyle t=\frac{{4V}}{{3V}}=\frac{4}{3} saat olarak bulunur.
Yolun yarısı \displaystyle =\frac{x}{2}=V.t\Rightarrow \frac{x}{2}=V.\frac{4}{3}\Rightarrow x=\frac{{8V}}{3}
Tüm yolu yürürse geçen süre \displaystyle =\frac{x}{V}=\frac{{\frac{{8V}}{3}}}{V}=\frac{8}{3} saat bulunur.
Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 7

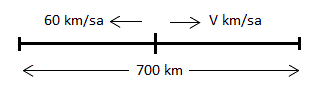
hrkt_prb_s14rl

İki araç zıt yönlerde hareket edince hızları toplamı kadar birbirinden uzaklaşırlar. Buna göre;
\displaystyle x=({{V}_{1}}+{{V}_{2}}).t
\displaystyle 700=(60+V).5
\displaystyle 140=60+V
\displaystyle V=80\text{ }km/sa bulunur.
Doğru Cevap : A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 6

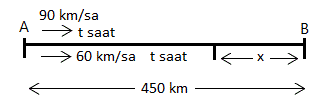
hrkt_prb_s12rl

Hızlı olan aracın yolu kaç saatte bitireceğini bulalım.
\displaystyle x=V.t
\displaystyle 450=90.t\text{ }\Rightarrow t=5 saat
5 saatte yavaş olan aracın ne kadar gideceğini bulalım.
\displaystyle x=V.t
\displaystyle x=60.5=300 km
Kalan yol \displaystyle =\text{ }450-300=150 km olarak bulunur.
Doğru Cevap: A şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 5

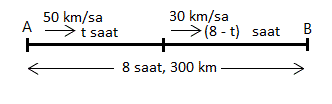
hrkt_prb_s10rl

Yolun 50 km/ sa hızla gidilen bölümü t saat sürmüşse, 30 km / sa hızla gidilen bölümde \displaystyle (8-t)
saat geçmiştir. Buna göre, iki farklı hızla gidilen yol denklemlerini, toplam yola eşitleyerek çözüme gidelim:
\displaystyle 300=50.t+30.(8-t)
\displaystyle 300=50t+240-30t
\displaystyle 300=20t+240
\displaystyle 60=20t
\displaystyle t=3 saat bulunur.
50 km/ sa ile gidilen yol \displaystyle =50.3=150 km dir.
Doğru Cevap : D şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 4

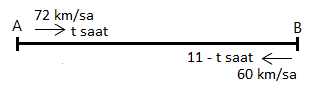
hrkt_prb_s8rl

Giderken geçen süreye t dersek, Dönüşte geçen süre \displaystyle 11-t saat olur.
Gidilen yol ile dönülen yol aynı olduğundan yol denklemlerini birbirine eşitleyelim,
\displaystyle 72.t=60.(11-t)
\displaystyle 72t=660-60t
\displaystyle 132t=660
\displaystyle t=5
İki şehir arası uzaklık \displaystyle =72.5=360 km saattir.
Doğru Cevap : E şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 3

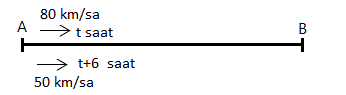
hrkt_prb_s6rl

Hızlı araç t sürede var dıysa, yavaş olan araç t + 6 saat sürede varmıştır.
İki aracın da gittiği yol aynı olduğundan iki yol denklemini birbirine eşitleyelim.
\displaystyle 80.t=50.(t+6)
\displaystyle 80t=50t+300
\displaystyle 30t=300
\displaystyle t=10\text{ }saat
\displaystyle \left| {AB} \right|=80.10=800 km olarak bulunur.
Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 2

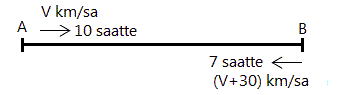
hrkt_prb_s4rl

A’dan B’ye gidilen yol ile geri dönülen yol aynı olduğundan bunları birbirine eşitleyerek çözüme ulaşabiliriz.
Gidilen Hıza V dersek,
Dönülen hız V+30 olur. Buna göre;
Gidilen yol = Dönülen yol
\displaystyle V.10=(V+30).7
\displaystyle 10V=7V+210
\displaystyle 3V=210
\displaystyle V=70\text{ }km/sa\text{ }bulunur.
\displaystyle \left| {AB} \right|=70.10=700\text{ }km olarak bulunur.
Doğru Cevap : B şıkkı

Soruyu Gör Sonraki Soru

ÇÖZÜM 1

Hareket problemlerinde \displaystyle x=V.t formülü kullanırız.
Burda x : gidilen yol, V: hız, t : süreyi ifade eder.
Bu soruda ilk baş yolun uzunluğunu bulalım,
\displaystyle x=V.t
\displaystyle x=120.6
\displaystyle =720 km dir.
Şimdi 90 km / sa hızla bu yolun kaç saatte alınacağını bulalım,
\displaystyle x=V.t
\displaystyle 720=90.t
\displaystyle t=\frac{{720}}{{90}}=8 saat olarak bulunur.
Doğru Cevap : C şıkkı

Soruyu Gör Sonraki Soru
Eğer çözümler konusunda anlaşılmayan bir yer görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.

Yorum yapın