Köklü Sayılar Soru ve Çözümleri 1 (Latex Formatı)

koklu_sayilar_gorseliBu bölümde Köklü Sayılar konusu ile ilgili 23 adet soru ve çözümleri bulunmaktadır. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…

 KÖKLÜ SAYILAR ÇÖZÜMLÜ SORULAR 1

SORU:1)


\displaystyle \text{2}\text{.}\sqrt[6]{{x+3}}+5.\sqrt[3]{{2x-16}}+\sqrt{{8-x}}

toplamının reel sayı olması için x’in alabileceği tam sayı değerlerinin toplamı kaçtır?

A) 23 B) 30 C) 35 D) 47 E) 58

ÇÖZÜM:

Köklü ifadenin derecesi çift ise içerdeki ifade negatif olmamalıdır. Tek derecelerde ise böyle bir sınırlamamız bulunmamaktadır. Buna göre;

\displaystyle 2.\underbrace{{\sqrt[6]{{x+3}}}}_{{\ge 0}}+5.\underbrace{{\sqrt[3]{{2x-16}}}}_{\begin{smallmatrix} s\imath n\imath rlama \\ \ \ \ yok \end{smallmatrix}}+\underbrace{{\sqrt{{8-x}}}}_{{\ge 0}}

Buna göre; \displaystyle x+3\ge 0\text{ }ve\text{ }8-x\ge 0  olmalıdır.

\displaystyle x\ge -3\text{ }ve\text{ }8\ge 0 dır. Yani;

\displaystyle x\text{ }[-3,8] aralığındaki tam sayı değerlerini alabilir.

Değerler toplamı:

\displaystyle \begin{array}{l}=\underbrace{{-3+(-2)+(-1)+0+1+2+3}}_{0}+4+5+6+7+8\\=30\text{ }buluruz.\end{array}

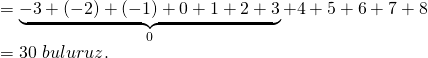
Doğru Cevap : B şıkkı

SORU:2)

\displaystyle \frac{{\sqrt{{2x-8}}+3x+\sqrt{{8-2x}}}}{{x+2}}

reel sayısının değeri kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6

ÇÖZÜM:

\displaystyle \frac{{\sqrt{{2x-8}}+3x+\sqrt{{8-2x}}}}{{x+2}}

ifadesinde köklü ifadelerin derecesi çift olduğundan içleri negatif olmamalıdır.
Buna göre;

\displaystyle \begin{array}{l}2x-8\ge 0\text{ }ve\text{ }8-2x\ge 0\text{ }olmal\imath d\imath r.\\\text{ }2x\ge 8\text{ }ve\text{ }8\ge 2x\text{ }\\\text{ }x\ge 4\text{ }ve\text{ }4\ge x\text{ }\end{array}

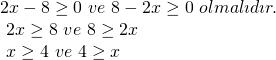
Bu şartlara uyan
tek bir x değeri var dır. O da x=4 tür. Buna
göre ifadenin değerini bulalım;
\displaystyle \begin{array}{l}\frac{{\sqrt{{2x-8}}+3x+\sqrt{{8-2x}}}}{{x+2}}=\frac{{\sqrt{{2.4-8}}+3.4+\sqrt{{8-2.4}}}}{{4+2}}\\=\frac{{0+12+0}}{6}=\frac{{12}}{6}=2\text{ }buluruz.\end{array}

Doğru Cevap : A şıkkı

SORU:3)

\displaystyle {{3}^{{\frac{4}{5}}}}  üslü sayısının köklü ifade olarak yazılmış şekli aşagıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }\sqrt{{{{3}^{4}}}}\text{ }} & {B)\text{ }\sqrt{{{{3}^{{\frac{4}{5}}}}}}} & {C)\text{ }\sqrt[5]{{{{3}^{4}}}}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }\sqrt[4]{{{{3}^{5}}}}} & {E)\text{ }\sqrt[2]{{{{3}^{5}}}}} \end{array}\end{array}

ÇÖZÜM:

Eğer bir sayının üssü kesirli sayı olarak ifade edilmişse paydadaki sayı kökün derecesini ifade eder. Pay ise normal kuvvetini ifade eder.

\displaystyle \begin{array}{l}{{\text{3}}^{{\frac{{4\to say\imath \text{ kuvveti}}}{{5\to k\ddot{o}k\text{ derecesi}}}}}}\text{ O halde;}\\{{\text{3}}^{{\frac{4}{5}}}}=\sqrt[5]{{{{3}^{4}}}}\text{ t }\!\!\ddot{\mathrm{u}}\!\!\text{ r}\text{. }\end{array}

Doğru Cevap: C şıkkı

SORU:4)

\displaystyle \sqrt[5]{{16}} köklü ifadesinin üslü sayı olarak yazılmış
şekli aşagıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }{{\text{2}}^{{\frac{1}{5}}}}\text{ }} & {B)\text{ }{{\text{2}}^{{\frac{2}{5}}}}} & {C)\text{ }{{\text{2}}^{{\frac{5}{4}}}}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }{{\text{2}}^{4}}} & {E)\text{ }{{\text{2}}^{{\frac{4}{5}}}}} \end{array}\end{array}

ÇÖZÜM:

\displaystyle \sqrt[5]{{16}} ifadesindeki 16’yı 2’nin üssü şeklinde yazalım,

\displaystyle \sqrt[5]{{16}}=\sqrt[5]{{{{2}^{4}}}}

Kökün derecesi, kesirli üssün paydasını oluşturur.Buna göre;

\displaystyle \sqrt[5]{{{{2}^{4}}}}={{2}^{{\frac{4}{5}}}} dir.

Doğru Cevap : E şıkkı

SORU:5)

\displaystyle \frac{{\sqrt[3]{{64}}+\sqrt[5]{{-32}}}}{{\sqrt[3]{{-8}}+\sqrt{9}}}

işleminin sonucu kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5

ÇÖZÜM:

Köklü ifadenin içindeki üslü sayının kuvveti ile kökün derecesi aynı olduğunda üslü sayının tabanı dışarıya çıkar. Buna göre; Köklü ifadelerin içini üslü sayı şeklinde ifade edelim;

\displaystyle \begin{array}{l}\frac{{\sqrt[3]{{64}}+\sqrt[5]{{-32}}}}{{\sqrt[3]{{-8}}+\sqrt{9}}}=\frac{{\sqrt[3]{{{{4}^{3}}}}+\sqrt[5]{{{{{(-2)}}^{5}}}}}}{{\sqrt[3]{{{{{(-2)}}^{3}}}}+\sqrt{{{{3}^{2}}}}}}\\\text{ }=\frac{{4+(-2)}}{{-2+3}}=\frac{2}{1}=2\text{ buluruz}\text{.}\end{array}

Doğru Cevap : B şıkkı

SORU:6)

\displaystyle \sqrt{{70-\sqrt{{20+8.\sqrt[3]{8}}}}}

işleminin sonucu kaçtır?
A) 4 B) 5 C) 6 D) 7 E) 8

ÇÖZÜM:

En içteki köklü ifadeyi çözmeye çalışarak en dışa
doğru adım adım gelelim.

\displaystyle \begin{array}{l}\sqrt{{70-\sqrt{{20+8.\sqrt[3]{8}}}}}=\sqrt{{70-\sqrt{{20+8.\sqrt[3]{{{{2}^{3}}}}}}}}\\\text{ }=\sqrt{{70-\sqrt{{20+8.2}}}}\\\text{ }=\sqrt{{70-\sqrt{{20+16}}}}\\\text{ }=\sqrt{{70-\sqrt{{36}}}}\\\text{ }=\sqrt{{70-6}}\\\text{ }=\sqrt{{64}}=8\text{ buluruz}\text{.}\end{array}

Doğru Cevap : E şıkkı

SORU:7)

\displaystyle \begin{array}{l}a<0<b\text{ }olmak\text{ }\ddot{u}zere,\\\text{ }\sqrt{{{{{(a-b)}}^{2}}}}+\sqrt[4]{{{{b}^{4}}}}+\sqrt[3]{{{{{(a-b)}}^{3}}}}\text{ }\end{array}

ifadesinin eşiti aşagıdakilerden hangisidir?
\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }a-b\text{ }} & {B)\text{ }a+b} & {C)\text{ }b} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }b-2a} & {\text{ }E)\text{ b}-a} \end{array}\end{array}

ÇÖZÜM:

Derecesi çift olan köklü ifadeler dışarıya mutlaka pozitif çıkar. Bunun için çift dereceli köklü sayıları dışarı çıkartırken mutlak değer içerisine almamız isabet olacaktır. Buna göre;

\displaystyle \begin{array}{l}\sqrt{{{{{(a-b)}}^{2}}}}+\sqrt[4]{{{{b}^{4}}}}+\sqrt[3]{{{{{(a-b)}}^{3}}}}=\left| {a-b} \right|+\left| b \right|+(a-b)\\\\\left| {a-b} \right|\Rightarrow a<0<b\text{ }\end{array}

olduğundan içerisi negatiftir. Bunun için mutlak değerden çıkarırken – ile çarparak çıkarmalıyız ki pozitif olsun.Buna göre;

\displaystyle \underbrace{{\left| {a-b} \right|}}_{{ici\text{ }negatif}}+\underbrace{{\left| b \right|}}_{{poz.}}+(a-b)=-a+b+b+a-b=b\text{ bulunur}

Doğru Cevap: C şıkkı

SORU:8)

3<x<5 olmak üzere,

\displaystyle \sqrt{{{{x}^{2}}-6x+9}}+\sqrt{{{{x}^{2}}-10x+25}}\text{ }

ifadesinin eşiti aşagıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ x}-3\text{ }} & {B)\text{ }2} & {C)\text{ }x-5} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }2x+2} & {\text{ }E)\text{ }2x-8} \end{array}\end{array}

ÇÖZÜM:

Derecesi çift olan köklü ifadeler dışarıya mutlaka pozitif çıkar. Bunun için çift dereceli köklü sayıları dışarı çıkartırken mutlak değer içerisine almamız isabet olacaktır.
Ayrıca soruda köklü ifade içerisinde verilen denklemlerin tam kare ifadeler olduğunu görüyoruz.

\displaystyle \begin{array}{l}{{x}^{2}}-6x+9={{(x-3)}^{2}}\\{{x}^{2}}-10x+25={{(x-5)}^{2}}\text{ O halde;}\\\\\sqrt{{{{x}^{2}}-6x+9}}+\sqrt{{{{x}^{2}}-10x+25}}=\sqrt{{{{{(x-3)}}^{2}}}}+\sqrt{{{{{(x-5)}}^{2}}}}\\=\underbrace{{\left| {x-3} \right|}}_{{ici\text{ pozitif}}}+\underbrace{{\left| {x-5} \right|}}_{\begin{smallmatrix} ici\text{ negatif} \\ -\text{ ile carp}\text{.} \end{smallmatrix}}=x-3-x+5=2\text{ buluruz}\text{.}\end{array}

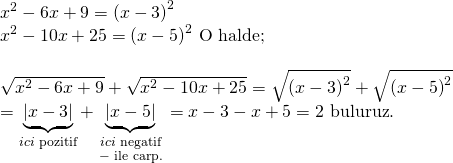
Doğru Cevap : B şıkkı

SORU:9)

\displaystyle \sqrt{{{{{\left( {2-\sqrt{5}} \right)}}^{2}}}}+\sqrt[3]{{{{{\left( {2-\sqrt{5}} \right)}}^{3}}}}+\sqrt[4]{{{{{\left( {2-\sqrt{9}} \right)}}^{4}}}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }1\text{ }} & {B)\text{ 3}-2\sqrt{5}} & {C)\text{ 4}-\sqrt{5}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }2\sqrt{5}} & {E)\text{ }6} \end{array}\end{array}

ÇÖZÜM:

Kök derecesi çift olan ifadeleri mutlak değer içerisinde; diğerlerini olduğu gibi dışarı çıkaralım. Buna göre;

\displaystyle \begin{array}{l}=\sqrt{{{{{\left( {2-\sqrt{5}} \right)}}^{2}}}}+\sqrt[3]{{{{{\left( {2-\sqrt{5}} \right)}}^{3}}}}+\sqrt[4]{{{{{\left( {2-\sqrt{9}} \right)}}^{4}}}}\\=\underbrace{{\left| {2-\sqrt{5}} \right|}}_{\begin{smallmatrix} ici\text{ negatif} \\ -\text{ ile carp} \end{smallmatrix}}+2-\sqrt{5}+\left| {2-\sqrt{9}} \right|\\=-2+\sqrt{5}+2-\sqrt{5}+\left| {2-3} \right|\\=0+\left| {-1} \right|\\=1\end{array}

Doğru Cevap: A şıkkı

SORU:10)

\displaystyle \sqrt{{81.{{{(x-5)}}^{2}}}}=27

denklemini sağlayan x değerlerinin çarpımı kaçtır?
A) 10 B) 12 C) 15 D) 16 E) 27

ÇÖZÜM:

Köklü ifadenin derecesi çift olduğu için dışarıya mutlak değer içerisinde çıkacaktır. Ama öncelikle köklü ifadenin içerisini tam kare olacak şekilde düzenleyelim.

\displaystyle \begin{array}{l}\sqrt{{81.{{{(x-5)}}^{2}}}}=27\text{ }\Rightarrow \sqrt{{{{9}^{2}}.{{{(x-5)}}^{2}}}}=27\\\text{ }\sqrt{{{{{\left[ {9.(x-5)} \right]}}^{2}}}}=27\\\text{ }\left| {9.(x-5)} \right|=27\\\text{ }9.\left| {(x-5)} \right|=27\\\text{ }\left| {(x-5)} \right|=3\text{ }\end{array}

Buna göre denklemin iki çözümü vardır

\displaystyle \begin{array}{l}Ya\text{ }x-5=3\text{ }ya\text{ }da\text{ }x-5=-3\text{ }t\ddot{u}r.\text{ }Buna\text{ }g\ddot{o}re\\\text{ }x=8\text{ }ya\text{ }da\text{ }x=2\text{ }dir.\end{array}

Köklerin çarpımı: 8.2 = 16 olarak bulunur.
Doğru Cevap : D şıkkı

SORU:11)

\displaystyle \sqrt[3]{{{{{(2x+7)}}^{3}}}}=9

denkleminin çözüm kümesi nedir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }\varnothing \text{ }} & {B)\text{ }\{-8\}} & {C)\text{ }\{1\}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }\{8,\text{ }1\}} & {E)\text{ }\{-8,\text{ }1\}} \end{array}\end{array}

ÇÖZÜM:

\displaystyle \sqrt[3]{{{{{(2x+7)}}^{3}}}}=9

eşitliğindeki köklü ifadenin dere –
cesi tek olduğundan kök içerisindeki ifade işare –
tine bakılmaksızın direkt dışarıya çıkar. Buna göre;

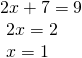\displaystyle \begin{array}{l}2x+7=9\\\text{ }2x=2\\\text{ }x=1\text{ }\end{array} bulunur.

O halde Ç.K.= {1} dir.

Doğru Cevap : C şıkkı

SORU:12)

\displaystyle \sqrt[4]{{{{{27}}^{{2x+1}}}}}=\sqrt[3]{{{{9}^{{x+7}}}}}

olduğuna göre, x kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }\frac{8}{7}\text{ }} & {B)\text{ }\frac{{47}}{{10}}} & {C)\text{ }\frac{{17}}{{10}}} & {D)\text{ }\frac{1}{2}} & {E)\text{ }\frac{3}{4}} \end{array}

ÇÖZÜM:

\displaystyle \sqrt[4]{{{{{27}}^{{2x+1}}}}}=\sqrt[3]{{{{9}^{{x+7}}}}}

eşitliğinde iki tarafı da üslü sayılar halinde gösterebiliriz.

\displaystyle \sqrt[4]{{{{{27}}^{{2x+1}}}}}=\sqrt[3]{{{{9}^{{x+7}}}}}\text{ }\Rightarrow \text{ }{{27}^{{\frac{{2x+1}}{4}}}}={{9}^{{\frac{{x+7}}{3}}}}

Daha sonra bu iki üslü sayıyı, aynı tabanın üslü sayısı olarak yazalım. \displaystyle 27\text{ }say\imath s\imath \text{ }{{3}^{3}}\text{ }ve\text{ }9\text{ }da\text{ }{{3}^{2}} olduğundan iki tarafı da 3 tabanında ifade edebiliriz.

\displaystyle \begin{array}{l}{{27}^{{\frac{{2x+1}}{4}}}}={{9}^{{\frac{{x+7}}{3}}}}\text{ }\Rightarrow \text{ }{{\left( {{{3}^{3}}} \right)}^{{\frac{{2x+1}}{4}}}}={{\left( {{{3}^{2}}} \right)}^{{\frac{{x+7}}{3}}}}\\\text{ }{{3}^{{3.\left( {\frac{{2x+1}}{4}} \right)}}}={{3}^{{2.\left( {\frac{{x+7}}{3}} \right)}}}\\\text{ }{{3}^{{\frac{{6x+3}}{4}}}}={{3}^{{\frac{{2x+14}}{3}}}}\\\text{ }\frac{{6x+3}}{4}=\frac{{2x+14}}{3}\\\text{ }18x+9=8x+56\\\text{ }10x=47\\\text{ }x=\frac{{47}}{{10}}\text{ }olarak\text{ }bulunur.\end{array}

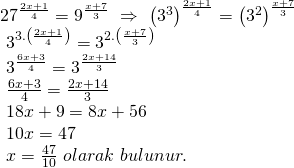
Doğru Cevap : B şıkkı

SORU:13)

\displaystyle \sqrt{{2+\frac{{14}}{{25}}}}-\sqrt{{1-\frac{7}{{16}}}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }0\text{ }} & {B)\text{ }1} & {C)\text{ }\frac{3}{4}} & {D)\text{ }\frac{9}{{10}}} & {E)\text{ }\frac{{\text{17}}}{{20}}} \end{array}

ÇÖZÜM:

İlk önce köklü ifadelerin içerisinde düzenleme yapalım,

\displaystyle \begin{array}{l}\sqrt{{2+\frac{{14}}{{25}}}}-\sqrt{{1-\frac{7}{{16}}}}=\sqrt{{\underset{{(25)}}{\mathop{{\frac{2}{1}}}}\,+\underset{{(1)}}{\mathop{{\frac{{14}}{{25}}}}}\,}}-\sqrt{{\underset{{(16)}}{\mathop{{\frac{1}{1}}}}\,-\underset{{(1)}}{\mathop{{\frac{7}{{16}}}}}\,}}\\\text{ }=\sqrt{{\frac{{50+14}}{{25}}}}-\sqrt{{\frac{{16-7}}{{16}}}}\\\text{ }=\sqrt{{\frac{{64}}{{25}}}}-\sqrt{{\frac{9}{{16}}}}\\\text{ }=\underset{{(4)}}{\mathop{{\frac{8}{5}}}}\,-\underset{{(5)}}{\mathop{{\frac{3}{4}}}}\,\\\text{ }=\frac{{32}}{{20}}-\frac{{15}}{{20}}=\frac{{17}}{{20}}\text{ olarak bulunur}\end{array}

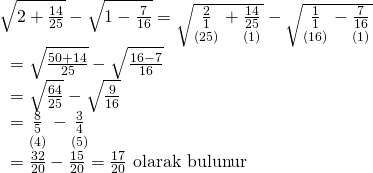
Doğru Cevap : E şıkkı

SORU:14)

\displaystyle \sqrt{{0,81}}-\sqrt{{0,04}}+\sqrt[3]{{0,001}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{*{20}{l}} {A)\text{ }\frac{3}{5}\text{ }} & {B)\text{ }\frac{4}{5}} & {C)\text{ }\frac{9}{{10}}} & {D)\text{ }1} & {E)\text{ }\frac{6}{5}} \end{array}

ÇÖZÜM:

Ondalık kesirleri rasyonel sayılara çevirerek çözüme başlayalım,

\displaystyle \begin{array}{l}\sqrt{{0,81}}-\sqrt{{0,04}}+\sqrt[3]{{0,001}}=\sqrt{{\frac{{81}}{{100}}}}-\sqrt{{\frac{4}{{100}}}}+\sqrt[3]{{\frac{1}{{1000}}}}\\\text{ }=\sqrt{{{{{\left( {\frac{9}{{10}}} \right)}}^{2}}}}-\sqrt{{{{{\left( {\frac{2}{{10}}} \right)}}^{2}}}}+\sqrt[3]{{{{{\left( {\frac{1}{{10}}} \right)}}^{3}}}}\\\text{ }=\frac{9}{{10}}-\frac{2}{{10}}+\frac{1}{{10}}\\\text{ }=\frac{{9-2+1}}{{10}}\\\text{ }=\frac{8}{{10}}=\frac{4}{5}\text{ }olarak\text{ }bulunur.\end{array}

Doğru Cevap : B şıkkı

SORU:15)

\displaystyle \left. \begin{array}{l}\sqrt{{108}}=a\sqrt{3}\\\sqrt{{32}}=b\sqrt{2}\end{array} \right\}

olduğuna göre a + b kaçtır?

A) 4 B) 5 C) 6 D) 8 E) 10

ÇÖZÜM:

Köklü ifadeleri çarpanlarına ayırarak yazalım,

\displaystyle \begin{array}{l}\sqrt{{108}}=a\sqrt{3}\text{ }\Rightarrow \sqrt{{36.3}}=a\sqrt{3}\text{ }\Rightarrow \sqrt{{{{6}^{2}}.3}}=a\sqrt{3}\\\text{ }\Rightarrow 6\sqrt{3}=a\sqrt{3}\text{ }\Rightarrow \text{ a=6 bulunur}\text{. }\\\sqrt{{32}}=b\sqrt{2}\text{ }\Rightarrow \sqrt{{16.2}}=b\sqrt{2}\text{ }\Rightarrow \sqrt{{{{4}^{2}}.2}}=b\sqrt{2}\\\text{ }\Rightarrow 4\sqrt{2}=b\sqrt{2}\text{ }\Rightarrow \text{ b=4 bulunur}\text{. }\end{array}

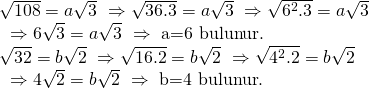
Buna göre;
a + b = 6 + 4 = 10 buluruz..
Doğru Cevap : E şıkkı

SORU:16)

\displaystyle \begin{array}{*{20}{l}} {a=\sqrt{{10}}} \\ {b=\sqrt[3]{{20}}} \\ {c=\sqrt[4]{{30}}} \end{array}

olduğuna göre, aşağıdaki sıralamalardan hangisi doğrudur?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }a<b<c\text{ }} & {B)\text{ }a<c<b} & {C)\text{ }b<a<c} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }c<a<b} & {E)\text{ }c<b<a} \end{array}\end{array}

ÇÖZÜM:

Köklü ifadeleri birbiriyle kıyas edebilmemiz için kök derecelerinin aynı olması gerekiyor. Bunun için köklü ifadeleri genişletip sadeleştirebiliriz. Buradaki köklü ifadelerin dereceleri sırasıyla 2,3 ve 4 olarak gözüküyor. Hepsinin derecesini 12
yapacak şekilde genişletelim.

\displaystyle \begin{array}{*{20}{l}} {a=\sqrt{{10}}=\sqrt[{2.6}]{{{{{10}}^{6}}}}=\sqrt[{12}]{{{{{10}}^{6}}}}=\sqrt[{12}]{{{{{10}}^{6}}}}=\sqrt[{12}]{{{{{1000.10}}^{3}}}}} \\ {b=\sqrt[3]{{20}}=\sqrt[{3.4}]{{{{{20}}^{4}}}}=\sqrt[{12}]{{{{{20}}^{4}}}}=\sqrt[{12}]{{{{2}^{4}}{{{.10}}^{4}}}}=\sqrt[{12}]{{{{{160.10}}^{3}}}}} \\ {c=\sqrt[4]{{30}}=\sqrt[{4.3}]{{{{{30}}^{3}}}}=\sqrt[{12}]{{{{{30}}^{3}}}}=\sqrt[{12}]{{{{3}^{3}}{{{.10}}^{3}}}}=\sqrt[{12}]{{{{{27.10}}^{3}}}}} \end{array}

Dereceler eşit olduğunda kökün içerisindeki ifade büyükse o sayı daha büyüktür. Buna göre;

\displaystyle \sqrt[{12}]{{{{{27.10}}^{3}}}}<\sqrt[{12}]{{{{{160.10}}^{3}}}}<\sqrt[{12}]{{{{{1000.10}}^{3}}}}\text{ }\Rightarrow \text{ }c<b<a\text{ }

Doğru Cevap : E şıkkı

SORU:17)

\displaystyle \sqrt{{108}}+\sqrt{{75}}-\sqrt{{12}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ 5}\sqrt{3}\text{ }} & {B)\text{ 7}\sqrt{3}} & {C)\text{ 9}\sqrt{3}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ 11}\sqrt{3}} & {E)\text{ 13}\sqrt{3}} \end{array}\end{array}

ÇÖZÜM:

Köklü sayılarda toplama çıkarma yapabilmek için köklü ifadelerin dereceleri ve içerisindeki değerler aynı olmalı. Bu soruda dereceler aynı ancak; kök içerindeki değerler birbirinden farklıdır. Bunun için kökün içerisini aynı yapmaya çalışalım. 108 , 75 ve 12 sayıları 3’ün katı olduğu için bu sayıları \displaystyle \sqrt{3} ‘lü olarak ifade edebiliriz. Şöyle ki;

\displaystyle \begin{array}{l}\sqrt{{108}}=\sqrt{{36.3}}=6\sqrt{3}\\\sqrt{{75}}=\sqrt{{25.3}}=5\sqrt{3}\\\sqrt{{12}}=\sqrt{{4.3}}=2\sqrt{3}\text{ Buna g }\!\!\ddot{\mathrm{o}}\!\!\text{ re;}\\\sqrt{{108}}+\sqrt{{75}}-\sqrt{{12}}=6\sqrt{3}+5\sqrt{3}-2\sqrt{3}\\\text{ }=(6+5-2).\sqrt{3}\\\text{ }=9\sqrt{3}\text{ olarak bulunur}\text{.}\end{array}

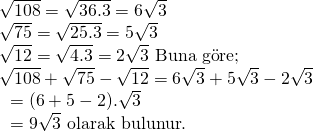
Doğru Cevap : C şıkkı

SORU:18)

\displaystyle \sqrt{{22,5}}-\sqrt{{8,1}}-\sqrt{{0,9}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ 3}\sqrt{{0,1}}\text{ }} & {B)\text{ 6}\sqrt{{0,1}}} & {C)\text{ 9}\sqrt{{0,1}}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ 11}\sqrt{{0,1}}} & {E)\text{ 13}\sqrt{{0,1}}} \end{array}\end{array}

ÇÖZÜM:

\displaystyle \sqrt{{22,5}}-\sqrt{{8,1}}-\sqrt{{0,9}}\text{ }

köklü ifadeler içerisindeki değerleri 0,1’in çarpanı olarak ifade edersek sayıların diğer çarpanlarını kökten kurtarabiliriz. Şöyle ki;

\displaystyle \begin{array}{l}=\sqrt{{22,5}}-\sqrt{{8,1}}-\sqrt{{0,9}}\\=\sqrt{{225x0,1}}-\sqrt{{81x0,}}1-\sqrt{{9x0,1}}\\=\sqrt{{{{{15}}^{2}}x0,1}}-\sqrt{{{{9}^{2}}x0,}}1-\sqrt{{{{3}^{2}}x0,1}}\\=15\sqrt{{0,1}}-9\sqrt{{0,1}}-3\sqrt{{0,1}}\\=(15-9-3).\sqrt{{0,1}}\\=3\sqrt{{0,1}}\text{ }olarak\text{ }bulunur.\text{ }\end{array}

Doğru Cevap : A şıkkı

SORU:19)

\displaystyle \sqrt{5}.\sqrt{6}.\sqrt{{15}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ 75}\sqrt{6}\text{ }} & {B)\text{ 25}\sqrt{3}} & {C)\text{ 10}\sqrt{6}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ 15}\sqrt{6}} & {E)\text{ 15}\sqrt{2}} \end{array}\end{array}

ÇÖZÜM:

Köklü ifadelerin dereceleri eşit ise içerideki değerleri aynı kökün içerisinde çarpabiliriz. Buna göre;

\displaystyle \begin{array}{l}\sqrt{5}.\sqrt{6}.\sqrt{{15}}=\sqrt{{5.6.15}}\\\text{ }=\sqrt{{450}}\\\text{ }=\sqrt{{225.2}}\\\text{ }=15\sqrt{2}\text{ olarak bulunur}\text{.}\end{array}

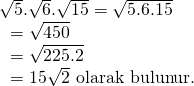
Doğru Cevap : E şıkkı

SORU:20)

\displaystyle \sqrt[4]{{{{2}^{3}}}}.\sqrt[3]{{{{2}^{4}}}}

işleminin sonucu kaçtır?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }\sqrt[{12}]{{{{2}^{7}}}}\text{ }} & {B)\text{ }\sqrt[{12}]{{{{2}^{{12}}}}}} & {C)\text{ }4\sqrt[{12}]{2}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }4\sqrt[{12}]{{{{2}^{5}}}}} & {E)\text{ }2\sqrt[{12}]{2}} \end{array}\end{array}

ÇÖZÜM:

Köklü ifadelerin dereceleri aynı olmadığı için direkt çarpamayız. Bunun için köklü ifadelerin derecelerini genişletelim. 3. ve 4. dereceden köklü ifadeleri dereceleri 12 olacak şekilde genişletebiliriz. Buna göre;

\displaystyle \begin{array}{l}\sqrt[4]{{{{2}^{3}}}}.\sqrt[3]{{{{2}^{4}}}}=\sqrt[{4.3}]{{{{2}^{{3.3}}}}}.\sqrt[{3.4}]{{{{2}^{{4.4}}}}}\\\text{ }=\sqrt[{12}]{{{{2}^{9}}}}.\sqrt[{12}]{{{{2}^{{16}}}}}\\\text{ }=\sqrt[{12}]{{{{2}^{{25}}}}}=\sqrt[{12}]{{{{2}^{{24}}}.2}}\\\text{ }={{2}^{2}}.\sqrt[{12}]{2}=4\sqrt[{12}]{2}\text{ olarak buluruz}\text{.}\end{array}

Doğru Cevap : C şıkkı

SORU:21)

\displaystyle \text{ }{{\left( {\sqrt{2}+\sqrt{5}} \right)}^{2}}

ifadesinin eşiti aşağıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }2\sqrt{{10}}\text{ }} & {B)\text{ }7+2\sqrt{{10}}} & {C)\text{ }10+2\sqrt{{10}}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }25+\sqrt{{10}}} & {E)\text{ }25+2\sqrt{{10}}} \end{array}\end{array}

ÇÖZÜM:

Tam kareyi açıp, bütün çarpanları birbiriyle teker teker çarpalım;

\displaystyle \begin{array}{l}{{\left( {\sqrt{2}+\sqrt{5}} \right)}^{2}}=(\sqrt{2}+\sqrt{5}).(\sqrt{2}+\sqrt{5})\\\text{ }=\sqrt{2}.\sqrt{2}+\sqrt{2}.\sqrt{5}+\sqrt{5}.\sqrt{2}+\sqrt{5}.\sqrt{5}\\\text{ }=2+\sqrt{{10}}+\sqrt{{10}}+5\\\text{ }=7+2\sqrt{{10}}\text{ olarak bulunur}\text{.}\end{array}

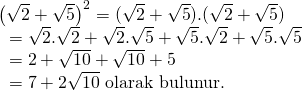
Doğru Cevap: B şıkkı

SORU:22)

\displaystyle \frac{{\sqrt{{24}}}}{{\sqrt{6}}}-\frac{{\sqrt{{75}}}}{{\sqrt{3}}}

işleminin sonucu aşağıdakilerden hangisidir?
A) 5 B) 3 C) 2 D) 2 E) 5

ÇÖZÜM:

Köklü ifadelerin dereceleri eşit ise direkt bölme işlemini kökün içerisinde gerçekleştirebiliriz. Buna göre;

\displaystyle \begin{array}{l}\frac{{\sqrt{{24}}}}{{\sqrt{6}}}-\frac{{\sqrt{{75}}}}{{\sqrt{3}}}=\sqrt{{\frac{{24}}{6}}}-\sqrt{{\frac{{75}}{3}}}\\\text{ }=\sqrt{4}-\sqrt{{25}}\\\text{ }=2-5=-3\text{ olarak bulunur}\text{.}\end{array}

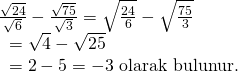
Doğru Cevap: B şıkkı

SORU:23)

\displaystyle \frac{{\sqrt[3]{4}.\sqrt{2}}}{{\sqrt[6]{{64}}}}

işleminin sonucu aşağıdakilerden hangisidir?

\displaystyle \begin{array}{l}\begin{array}{*{20}{l}} {A)\text{ }\sqrt[6]{2}\text{ }} & {B)\text{ }\sqrt[6]{8}} & {C)\text{ }\sqrt[6]{{16}}} \end{array}\\\begin{array}{*{20}{c}} {\text{ }D)\text{ }\sqrt[6]{{32}}} & {E)\text{ }\sqrt[6]{{48}}} \end{array}\end{array}

ÇÖZÜM:

Bölme işlemini yapabilmek için köklü ifadelerin derecelerinin birbirine eşit olması gerekir. Bu soruda köklerin derecelerini 6 yapacak şekilde genişletelim;

\displaystyle \begin{array}{l}\frac{{\sqrt[3]{4}.\sqrt{2}}}{{\sqrt[6]{{64}}}}=\frac{{\sqrt[{3.2}]{{{{4}^{2}}}}.\sqrt[{2.3}]{{{{2}^{3}}}}}}{{\sqrt[6]{{64}}}}\\\text{ }=\sqrt[6]{{\frac{{{{4}^{2}}{{{.2}}^{3}}}}{{64}}}}\\\text{ }=\sqrt[6]{{\frac{{16.8}}{{64}}}}\\\text{ }=\sqrt[6]{{\frac{{128}}{{64}}}}\\\text{ }=\sqrt[6]{2}\text{ olarak bulunur}\text{.}\end{array}

Doğru Cevap : A şıkkı

Yorum yapın