 Bu bölümde 1.Dereceden Denklemler ile ilgili 30 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
Bu bölümde 1.Dereceden Denklemler ile ilgili 30 adet soru bulunmaktadır. Sorularınızı çözdükten sonra “Doğru Cevap” seçeneğine tıklayarak doğru şıkkı görebilirsiniz. Eğer soruları çözmekte zorlanırsanız; kolay anlaşılır detaylı çözümlere “Çözüm için Tıklayınız” seçeneği ile ulaşabilirsiniz. Sorular Latex formatında hazırlanarak görünüm iyileştirilmiştir. İyi Çalışmalar…
SORULAR
SORU 1
![]()
denklemi x değişkenine bağlı birinci dereceden bir bilinmeyenli bir denklem olduğuna göre, bu denklemi sağlayan x değeri kaçtır?
A) -1 B) -2 C) -3 D) -4 E) -5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 2
a bir reel sayı olmak üzere, x değişkenine bağlı birinci dereceden bir bilinmeyenli ![]() denkleminin çözüm kümesi aşağıdakilerden hangisidir?
denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) {1} B) {2} C) {3} D) {4} E) {5}
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 3
![]()
denklemini sağlayan x değeri kaçtır?
A) -1 B) -2 C) -3 D) -4 E) -5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 4
![]()
olduğuna göre, x kaçtır?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 5
![]()
olduğuna göre, x kaçtır?
A) 5 B) 10 C) 15 D) 16 E) 20
| Doğru Cevap | Çözüm için Tıklayınız |
Eğer sorular ya da çözümler konusunda bir problem görür veyahut da bir tavsiye de bulunmak isterseniz; sayfanın en altında yer alan “Yorum Yap” seçeneği ile bunları anlık olarak iletebilirsiniz.
SORU 6
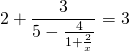
eşitliğine göre x kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 7
![]()
x değişkenine bağlı yukarıdaki denklemin kökü 2 olduğuna göre, a kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 8
![]() olmak üzere,
olmak üzere,
![]()
denklemini sağlayan x değeri kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 9
m ve n birer gerçel sayı olmak üzere,
![]()
denkleminin x e bağlı sonsuz çözümü olduğuna göre, m + n kaçtır?
A) 3 B) 1 C) 1 D) 2 E) 3
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 10
![]()
denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) { 1} B) {1} C) {0} D) Ø E) R
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 11
![]()
denkleminin çözüm kümesi aşağıdakilerden hangisidir?
A) { 1} B) {1} C) {0} D) Ø E) R
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 12
a bir gerçel sayıdır.
![]()
denkleminin çözüm kümesi boş küme olduğuna göre, a kaçtır?
A) 2 B) 3 C) 4 D) 5 E) 6
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 13
x değişkenine bağlı
![]()
denkleminin çözüm kümesi tek elemanlı olduğuna göre, a kaç olamaz ?
![]()
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 14
x + 3y = 12
2x + y = 24
denklem sistemine göre, x kaçtır?
A) 10 B) 12 C) 13 D) 14 E) 15
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 15
![]()
![]()
olduğuna göre, x kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 16
Sırasıyla x ve y değişkenlerine bağlı
ax + by = 5
2bx – ay = 7
denklem sisteminin çözüm kümesi {( 2,1)} olduğuna göre, a + b kaçtır?
A) -5 B) -4 C) -3 D) -2 E) -1
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 17
ax – 2y + 1 = 0
9x + by + 3 = 0
denklem sistemi x ve y değişkenlerine bağlı sonsuz çözümü olduğuna göre, a – b kaçtır?
A) 3 B) 6 C) 9 D) 12 E) 15
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 18
3x – 2y + 5 = 0
6x – 4y + a = 0
denklem sisteminin çözüm kümesi boş küme olduğuna göre, a kaç olamaz ?
A) 2 B) 4 C) 6 D) 8 E) 10
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 19
3x – 2y + 5 = 0
6x + ay + 9 = 0
denklem sisteminin çözüm kümesi tek olduğuna göre, a kaç olamaz ?
A) 4 B) 2 C) 0 D) 2 E) 4
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 20
x = 2t + 1
y = 1 – 3t
parametreleriyle verilen x ve y değişkenlerine bağlı birinci dereceden iki bilinmeyenli denklem aşağıdakilerden hangisidir?
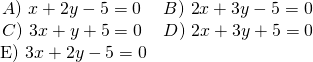
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 21
![]()
eşitliğine göre, x in y cinsinden eşiti aşağıdakilerden hangisidir?
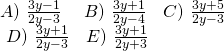
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 22
![]()
eşitliğine göre, y nin hangi değeri için x tanımsızdır?
A) -4 B) -1 C) 0 D) 2 E) 4
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 23
![]()
denklemi ∀ x, y R için sağlanıyorsa b kaçtır?
A) 3 B) 4 C) 7 D) 8 E) 9
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 24
![]()
denklemine göre, a.b çarpımı kaçtır?
A) 3 B) 4 C) 5 D) 7 E) 9
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 25
a + b = 5
a + c = 6
b + c = 7
olduğuna göre, a.b.c çarpımı kaçtır?
A) 24 B) 28 C) 32 D) 36 E) 40
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 26
![]()
![]()
![]()
olduğuna göre, a kaçtır?
A) 1 B) 2 C) 3 D) 4 E) 5
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 27
![]()
![]()
![]()
olduğuna göre, x.y.z çarpımı kaçtır?
A) 3 B) 4 C) 5 D) 6 E) 7
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 28
a + b = 3
olduğuna göre, a² + ab + 3b ifadesinin değeri kaçtır?
A) 3 B) 4 C) 5 D) 7 E) 9
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 29
x – 3y + 2z = 12
x – 7y + 3z = 5
olduğuna göre, x + y + z kaçtır?
A) 19 B) 22 C) 23 D) 25 E) 29
| Doğru Cevap | Çözüm için Tıklayınız |
SORU 30
2x – 3y + 2z = 12
x – 5y + 3z = 10
x – 8y + 5z = 14
olduğuna göre, x kaçtır?
A) 2 B) 3 C) 4 D) 6 E) 8
| Doğru Cevap | Çözüm için Tıklayınız |
SORU ÇÖZÜMLERİ
ÇÖZÜM 30
Denklem sistemini uygun katsayılarla genişletip x’i yalnız bırakmaya çalışalım.
![]()
![]()
![]()
![]()
![]()
![]()
![]() buluruz.
buluruz.
Doğru Cevap : C şıkkı
| Soruyu Gör |
ÇÖZÜM 29
3 bilinmeyenin olduğu denklem sisteminde bilinmeyenleri tek tek bulabilmek için en az 3 denkleme ihtiyaç vardır. Burada 2 denklem olduğundan tek tek bulmak mümkün değildir.
Bu soruda bizden istenen ifadeyi, verilen eşitlikleri uygun katsayılarla genişletip, taraf tarafa toplarsak bulabiliriz.
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 28
![]() ifadesinde a’lı terimleri ortak paranteze alalım.
ifadesinde a’lı terimleri ortak paranteze alalım.
![]()
![]() 9 buluruz.
9 buluruz.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 27
Bu denklem sistemini taraf tarafa çarpalım.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 26
Bu denklem sistemini taraf tarafa toplayalım.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 25
Bu denklem sistemini taraf tarafa toplayalım.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Buna göre; a.b.c = 2.3.4 = 24 bulunur.
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 24
![]()
İki terimin kareleri toplamının 0 olabilmesi için bu iki terimin de 0 olması lazımdır. Çünkü bir terim pozitif olursa diğer terim negatif olamaz. (Bir sayının karesi negatif
olamaz.)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bu durumda a.b = 1.7 = 7 bulunur.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 23
∀ işareti “Her” demektir.
∀ x, y R : Her x,y reel sayı değerleri için sağlanıyor demektir.
![]() denklemi her x,y için
denklemi her x,y için
sağlanıyor olması, x ve y nin önündeki katsayıların 0 olması ile sağlanır.
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : C şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 22
Eşitlikteki x’li terimleri biraraya getirelim.
![]()
![]()
![]()
![]()
![]()
Kesirli ifadenin paydası 0 olursa bu kesir tanımsız olur. Buna göre;
![]() olursa bu kesir tanımsızdır.
olursa bu kesir tanımsızdır.
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 21
Eşitlikteki x’li terimleri biraraya getirelim.
![]()
![]()
![]()
![]()
![]() buluruz.
buluruz.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 20
İki eşitlikte de t’leri yalnız bırakalım.
![]()
![]()
Şimdi iki t eşitliğini, birbirine eşitleyelim,
![]()
![]()
![]()
![]() denklemini buluruz.
denklemini buluruz.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 19
İki bilinmeyenli denklemlerde çözüm kümesinin tek olması için x’in önündeki katsayıların oranı, y’nin önündeki katsayıların oranına eşit olmamalıdır.
Buna göre;
![]()
![]()
![]()
O halde; a, -4’e eşit olamaz.
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 18
İki bilinmeyenli denklemlerde çözüm kümesinin boş küme olması için x’in önündeki katsayıların oranı, y’nin önündeki katsayıları oranına eşit olurken; sabit terimlerin oranına eşit olmamalıdır.
Buna göre;
![]()
![]()
![]()
O halde; a, 10’a eşit olamaz.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 17
İki bilinmeyenli denklemlerde sonsuz çözüm olması için x’in önündeki katsayıların oranı, y’nin önündeki katsayıları oranına; o da sabit terimlerin oranına eşit olmalıdır.
Buna göre;
![]()
![]()
![]()
![]()
O halde; ![]() buluruz.
buluruz.
Doğru Cevap : C şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 16
Çözüm kümesi {( 2,1)} olduğundan denklem sistemi x 2 ve y 1 için sağlanır. Bu değerleri denklem sisteminde yerlerine yazalım.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() idi.
idi. ![]()
![]() bulunur.
bulunur.
O halde; ![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 15
Bu denklemi çözmek için yerine koyma metodunu kullanalım.
y’yi x cinsinden ifade edip, y’nin yerine yazalım.
![]()
![]()
![]()
![]()
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 14
Denklem sistemindeki x’i, yok etme metodunu kullanarak bulmaya çalışalım. Bunun için y’yi yok etmeliyiz.
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 13
Denklemin çözüm kümesi tek elemanlı ise, x’in katsayısı 0 olamaz. Buna göre;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 12
Bir denklemin çözüm kümesi boş küme ise, bu denklemde x’in katsayısı 0 olmalı, diğer terimler ise 0’a eşit olmamalıdır. Buna göre;
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 11
İlk önce parantezleri açalım.
![]()
![]()
x’leri bir tarafta, diğerlerini bir tarafta toplayalım.
![]()
![]()
Buna göre; x’in hiç bir değeri için bu eşitlik sağlanamaz. Dolayısıyla çözim kümesi boş kümedir ve Ø ile gösterilir.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 10
İlk önce parantezleri açalım.
![]()
![]()
x’leri bir tarafta, diğerlerini bir tarafta toplayalım.
![]()
![]()
Buna göre; x’in her değeri için bu eşitlik sağlanır.Dolayısıyla çözim kümesi Reel sayılar kümesidir ve R ile gösterilir.
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 9
Denklemin çözüm kümesinin sonsuz olması için; denklemi düzenledikten sonra x’in önündeki katsayı 0 olmalı, ayrıca diğer terimler de 0 olmalıdır.
Buna göre denklemi düzenleyelim;
![]()
![]()
![]()
![]()
![]()
Buna göre; ![]() buluruz.
buluruz.
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 8
Eşitliğin iki tarafında da aynı çarpan varsa, bunları sadeleştirerek kolayca çözüme gidebiliriz.
![]()
(3x 7). (x 3)
![]()
![]()
![]() buluruz.
buluruz.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 7
Denklemin kökü 2 ise bu denklem x 2 için sağlanır. Bu sebeple x yerine 2 yazıp, a’yı bulabiliriz.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 6
Merdiven tipi kesirli sorularda adım adım geriye doğru gitmek gerekir.
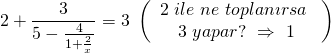
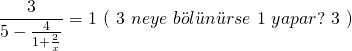
![]()
![]()
![]()
![]()
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 5
İlk önce paydaları eşitleyelim.
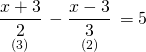
![]()
![]()
(Burada – yi yanlış dağıtmak en fazla yapılan hatalardandır. Buna dikkat edelim.)
![]()
![]()
![]()
![]() buluruz.
buluruz.
Doğru Cevap : C şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 4
Denklemi içler dışlar çarpımı yaparak çözeriz.
![]()
![]()
![]()
![]()
![]()
![]()
Doğru Cevap : A şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 3
Denklemde, ilk önce parantezlerden kurtulalım.
![]()
![]()
Sonra x’leri bir tarafta, Sayıları diğer tarafta toplayalım.
![]()
![]()
![]()
![]()
Doğru Cevap : E şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 2
Denklem, bir bilinmeyenli ve bu bilinmeyen x olduğuna göre; y’nin önündeki katsayı 0 olmalı.
![]()
![]()
Buna göre, yeni denklem;
![]()
![]()
![]()
![]()
Çözüm Kümesi: {2}
Doğru Cevap : B şıkkı
| Soruyu Gör | Sonraki Soru |
ÇÖZÜM 1
Denklem , birinci derence bir denklem olduğu için, x³ ve x² gibi birden yüksek dereceleri terimlerin katsayıları 0 olmalıdır.
![]()
![]()
![]()
Bu durumda yeni denklem;
![]()
![]()
![]()
![]()
![]()
![]() buluruz.
buluruz.
Doğru Cevap : D şıkkı
| Soruyu Gör | Sonraki Soru |


12 . soruda bı sorun olabilirmi a = 5 1.tarafta ama 2. tarafa 5 koyunca denklem aynı olmuyor yanlıs olabilirmi
Zaten eşit olmaması gerekiyor. Bu sebeple çözüm kümesi boş oluyor.
YAW BU NE bıcım sorular be