Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Zor çarpanlarına ayırma soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU

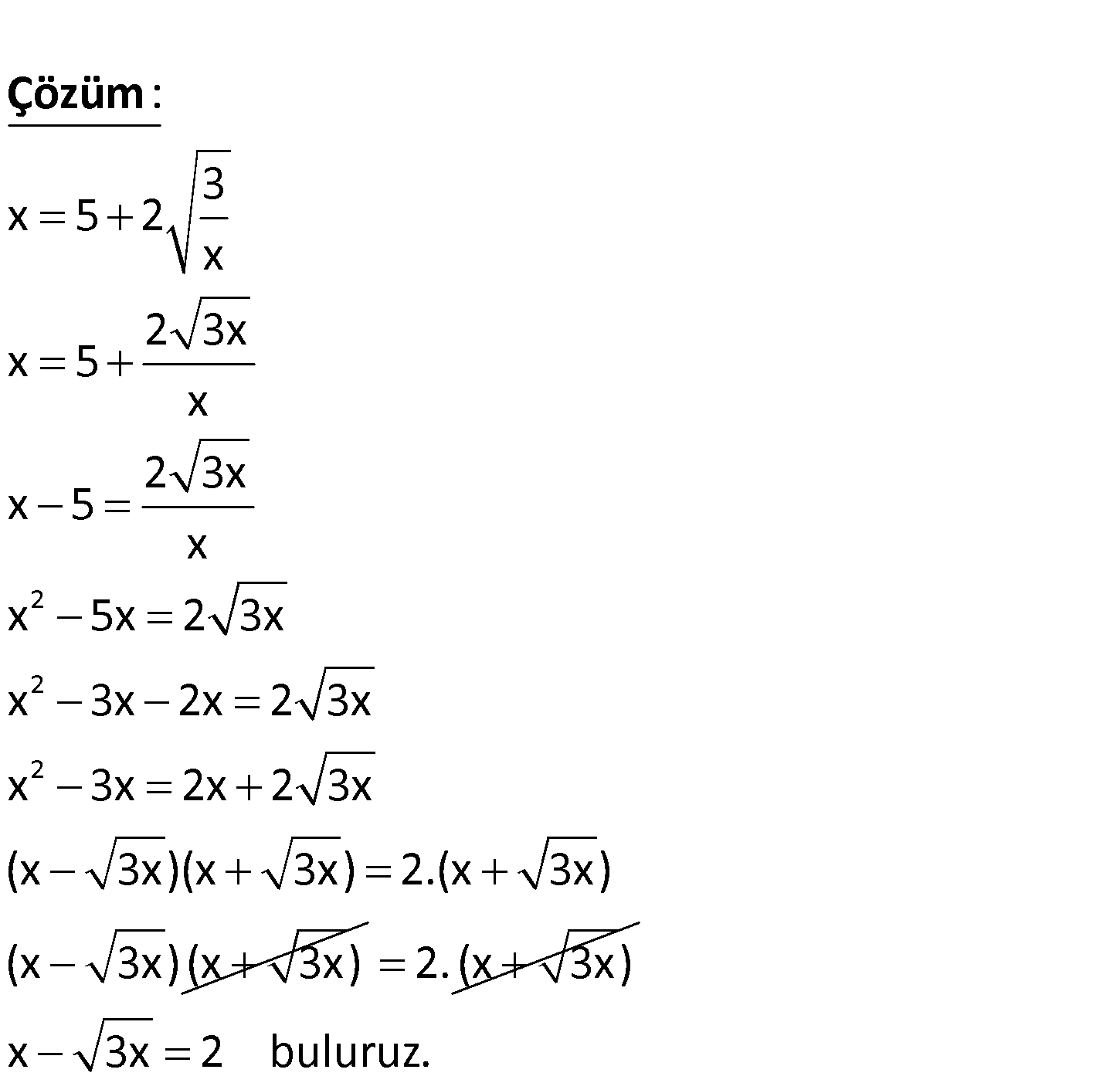
3.SORU


4.SORU
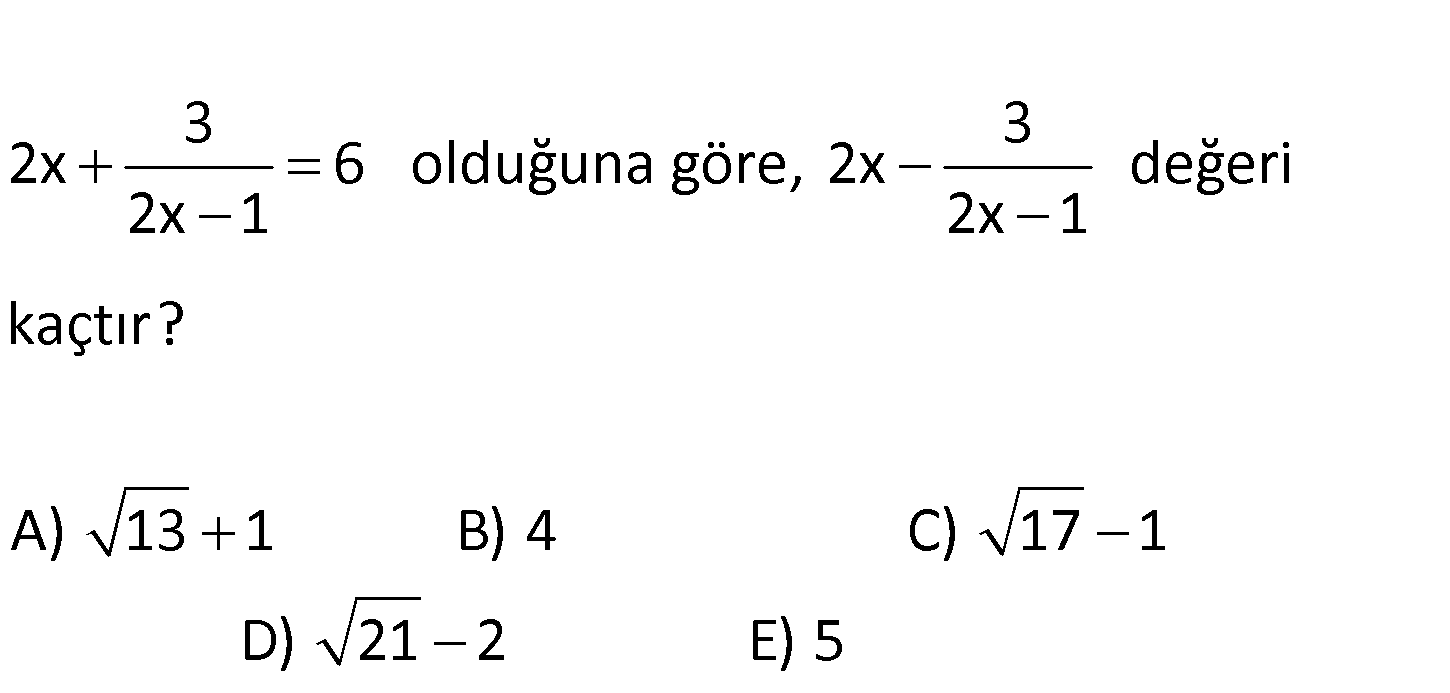
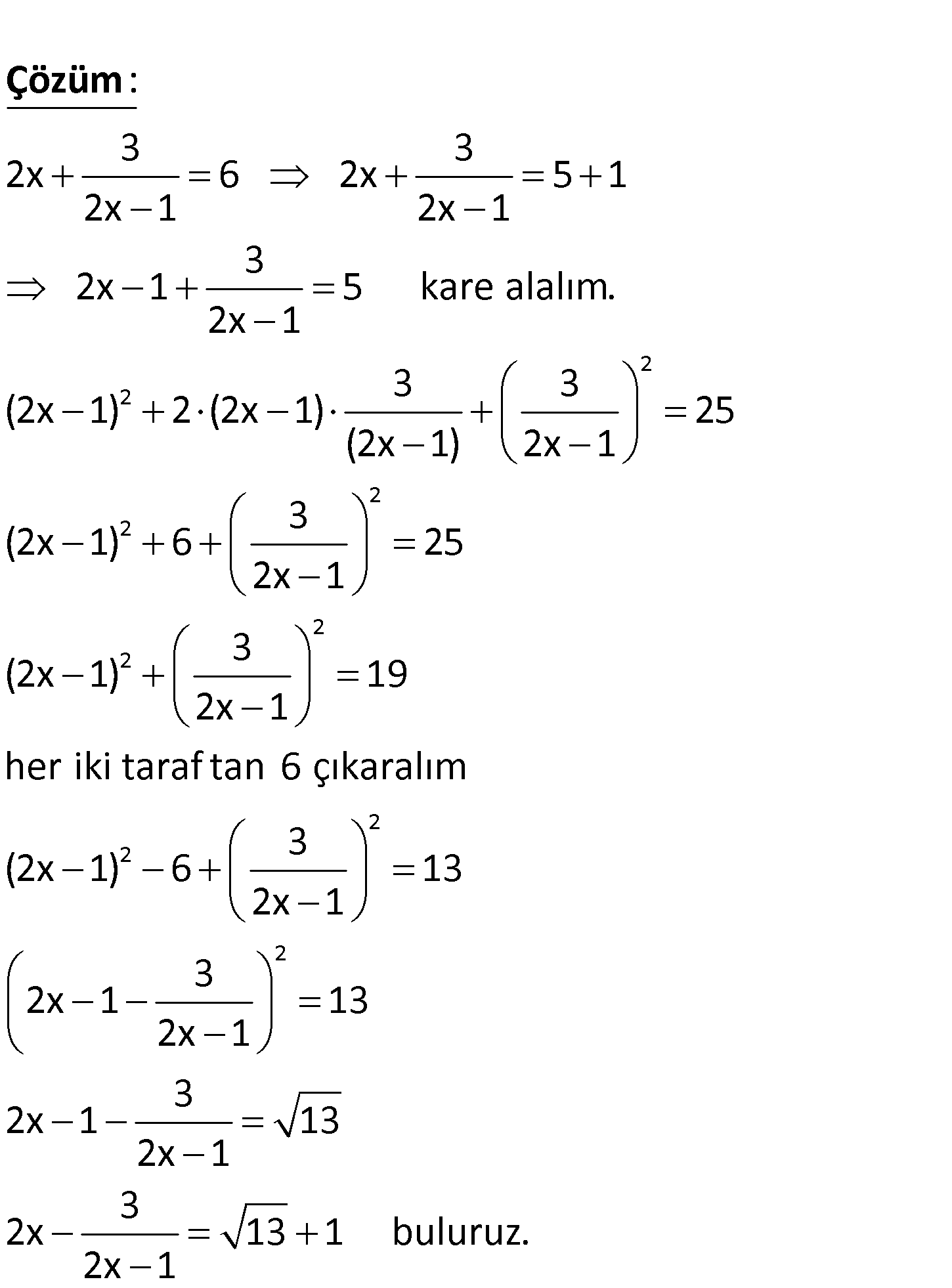
5.SORU
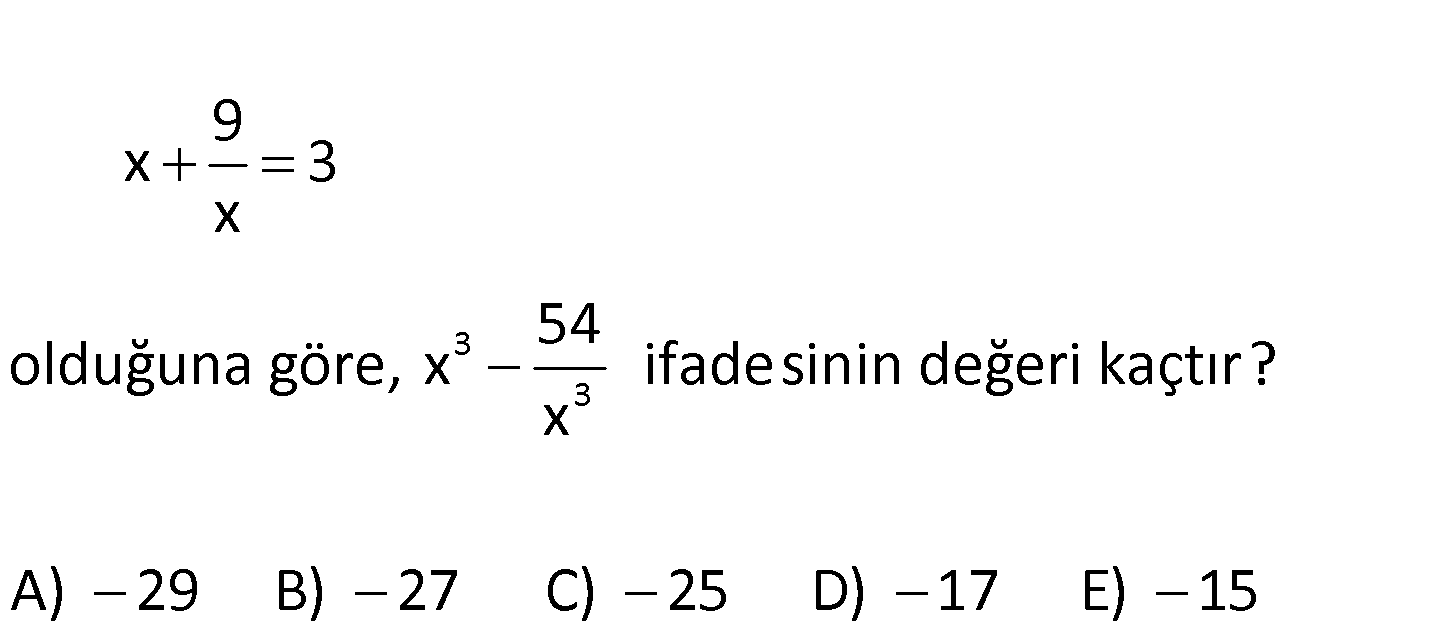
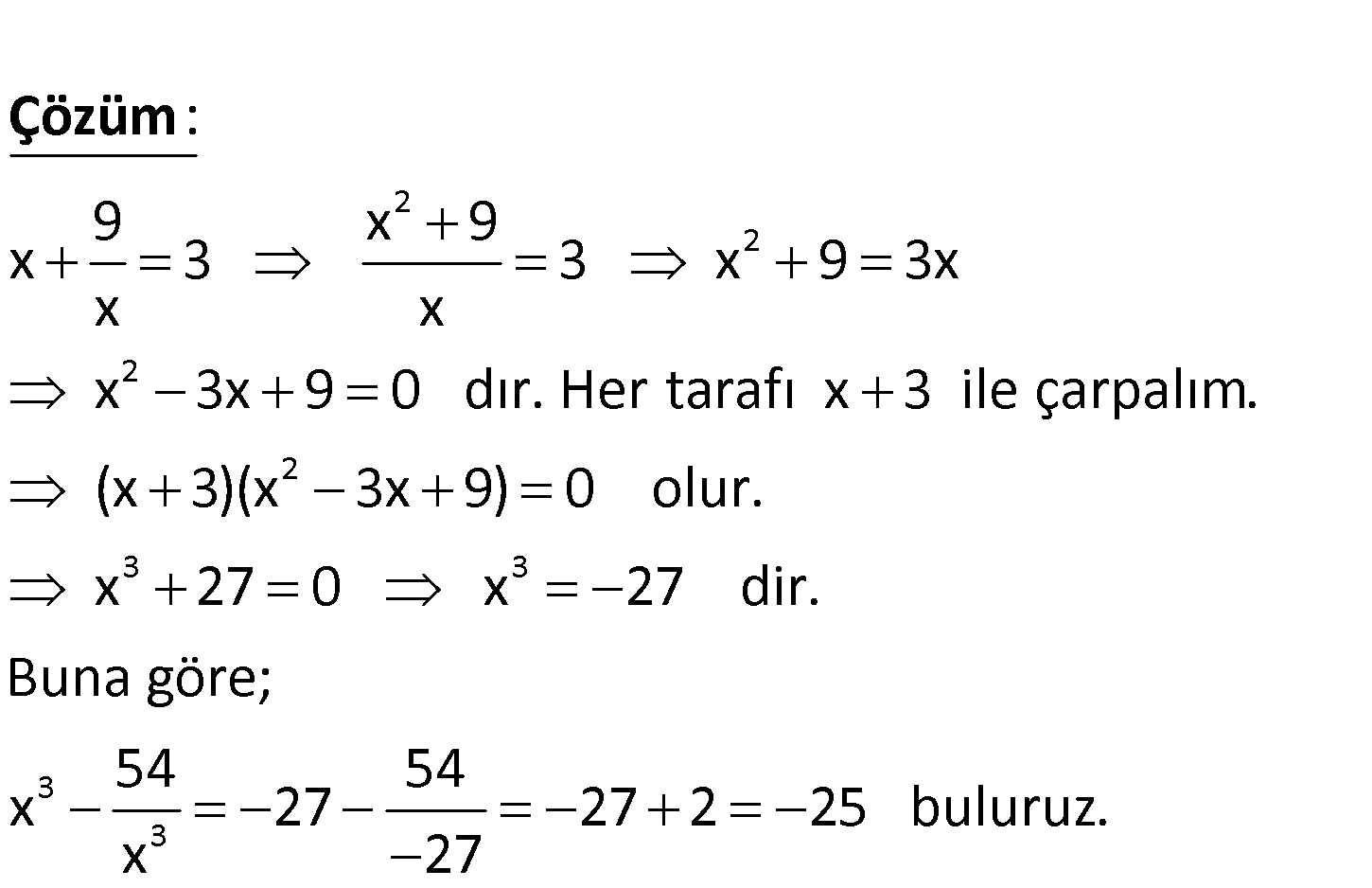
6.SORU


7.SORU


8.SORU

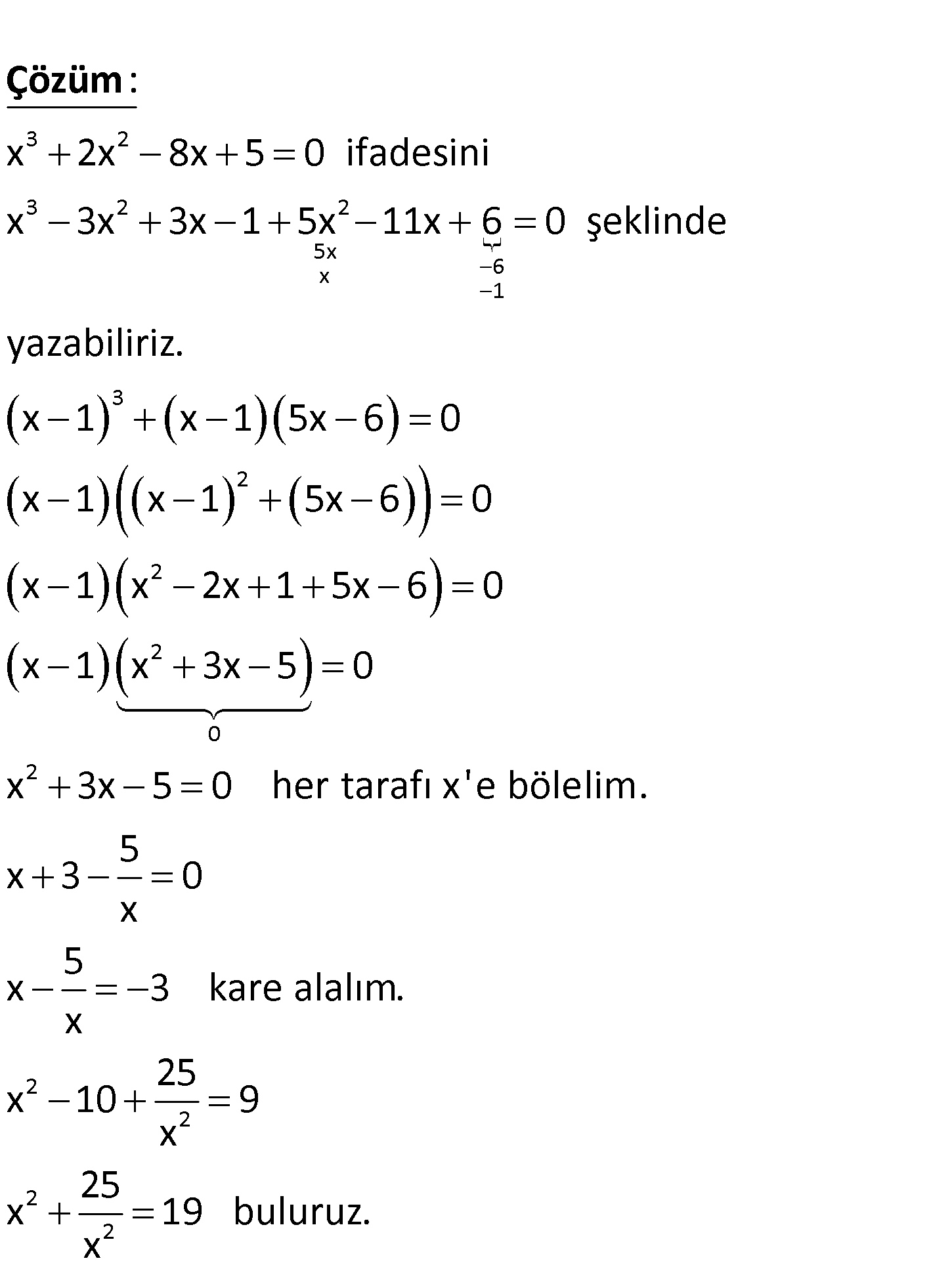
9.SORU
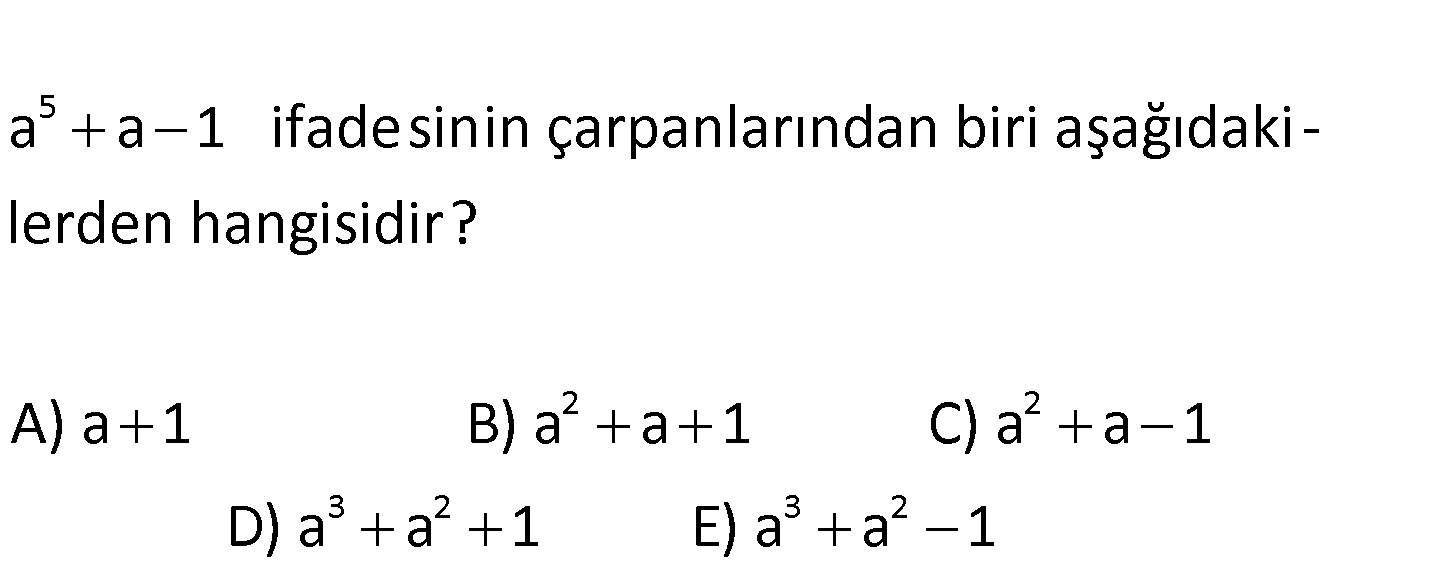

10.SORU

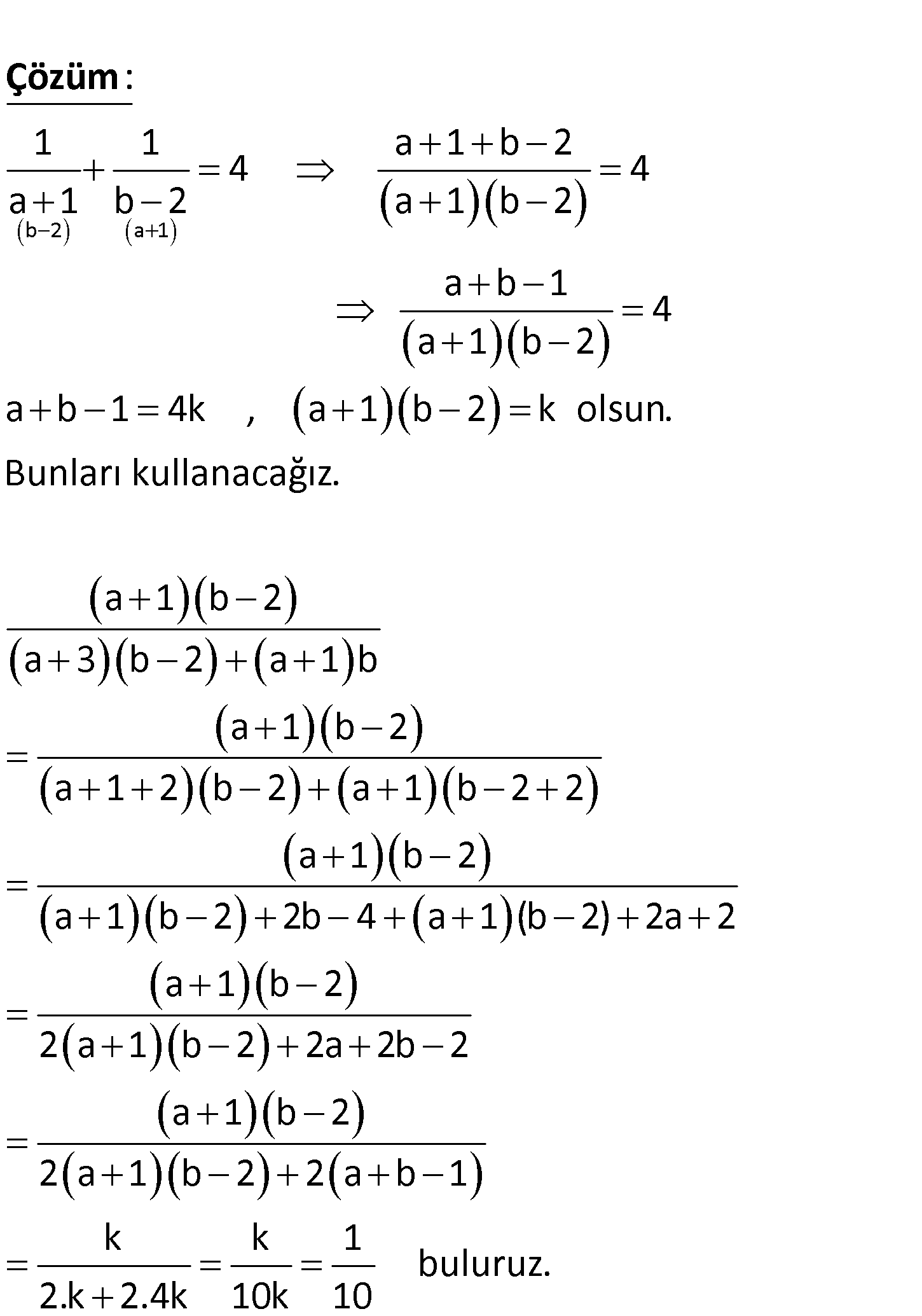
11.SORU
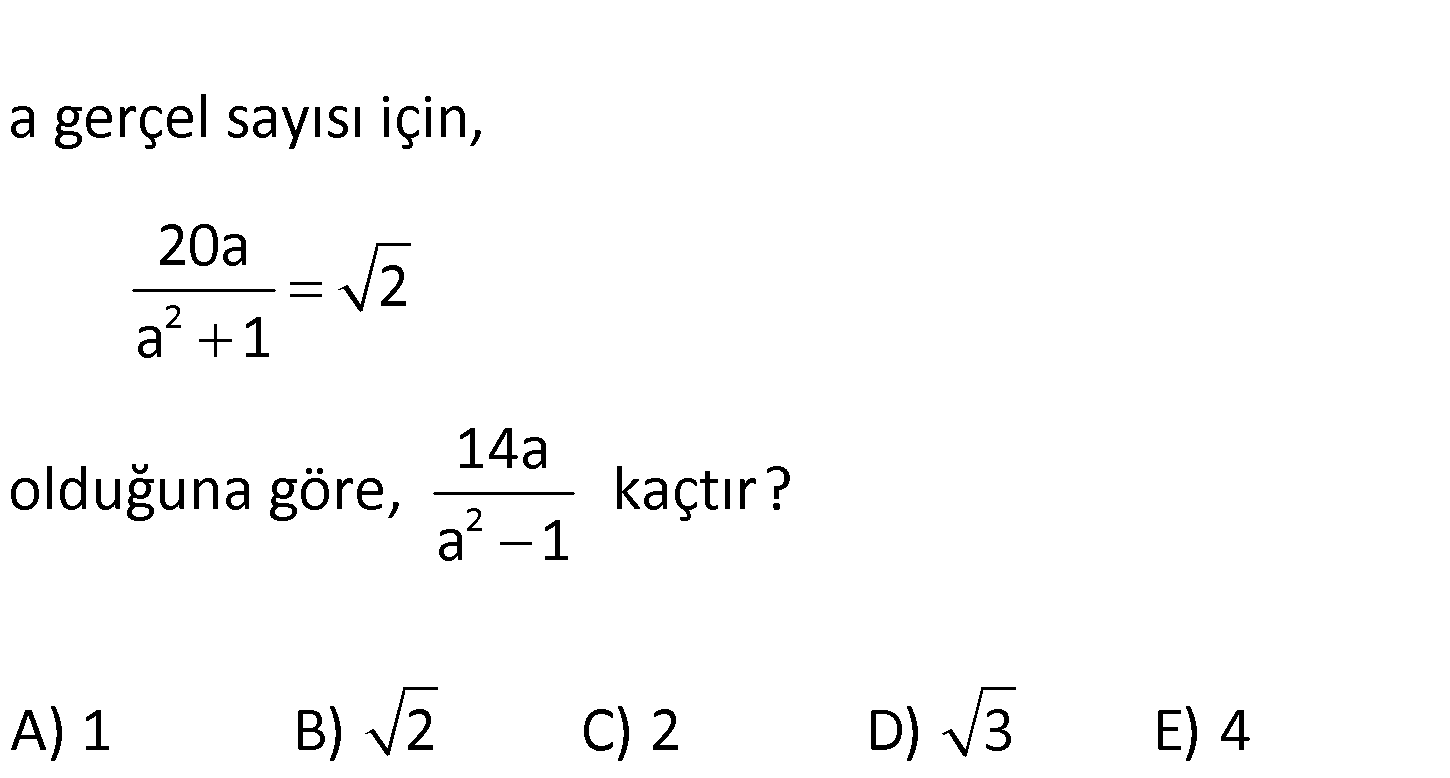

12.SORU
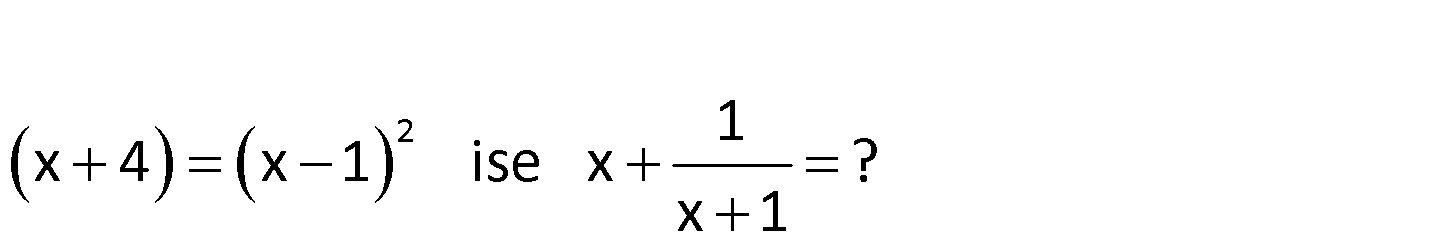
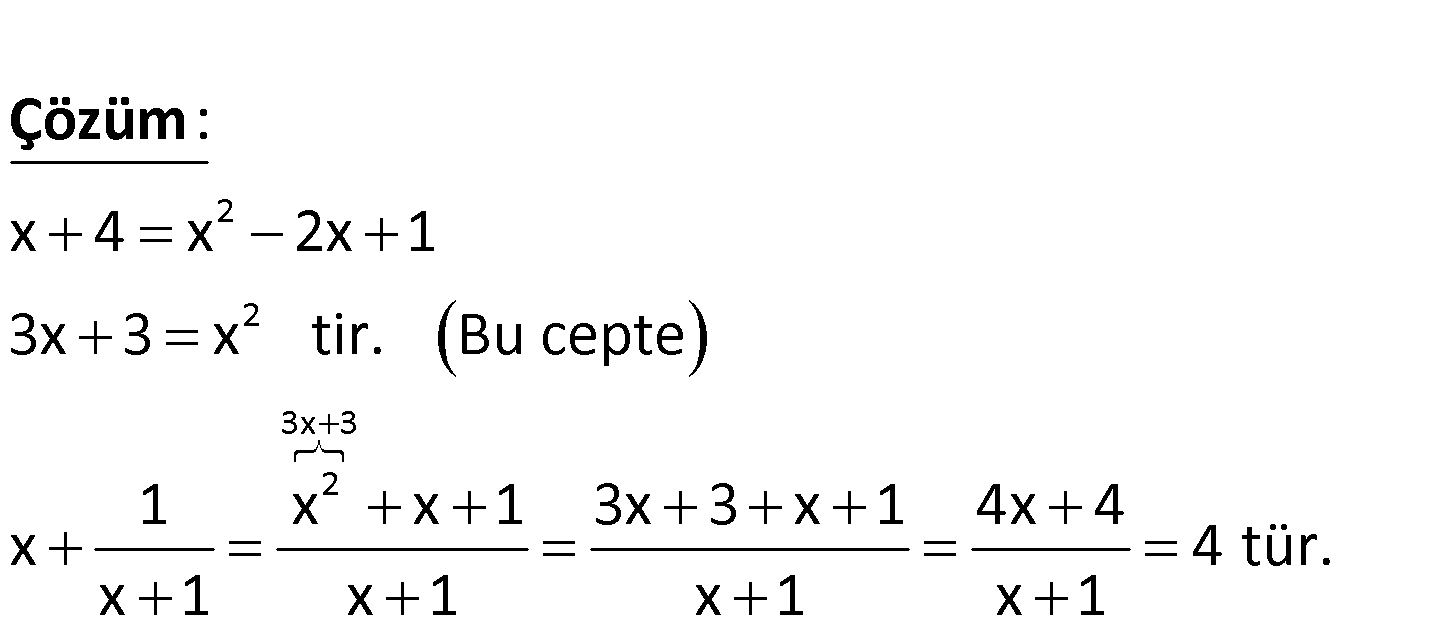
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 4 2 x 2x 33 0 ise x 4 ifadesinin değeri kaçtır? 5 x 2x 2 2 2 4 2 2 2 2 x 2x 33 0 x 33 2x tir. Kare alalım. x 33 132x 4x 33 132x 4(33 2x) 33 132 4 : x Çözüm 2 4 2 .33 8x 33 140x 132 1089 140x 132 1221 140x (x 4) (1221 140x 4) 5(x 2x 2) 5(33 2x 2x 2) 1225 140x 35(35 4x) 5(35 4x) 5(35 4x) 7 buluruz. www.matematikkolay.net 35
3 x 5 2 ise x x 3x ifadesi nin de ğeri ka ı çt r? www.matematikkolay.net 2 2 2 3 x 5 2 x 2 3x x 5 x 2 3x x 5 x x 5x 2 3x x 3x 2x 2 3x x 3x 2x 2 3x (x 3x)(x 3x) : 2.(x 3x) (x 3x) (x 3x) Çözüm 2. (x 3x) x 3x 2 buluruz. 37
2 2 a 2a 6 0 olduğuna göre, 12 a ifadesinin değeri kaçtır? a A) 10 B) 8 C) 6 D) 4 E) 2 2 2 2 a 2a 6 0 a 2a 6 (ifadeyi 2 ile genişletelim) 2a 4a 12 dir. Şimdi bulduğumuz ifadeyi bizd : Çözüm 2 2 2 2 6 en istenen ifadede 12 yerine yazalım. 12 2a 4a a a a 2a 4 10 buluruz. a a www.matematikkolay.net 41
www.matematikkolay.net 3 3 2x 6 olduğuna göre, 2x değeri 2x 1 2x 1 kaçtır? A) 13 1 B) 4 C) 17 1 D) 2 1 2 E) 5 2 3 3 2x 6 2x 5 1 2x 1 2x 1 3 2x 1 5 kare alalım. 2x 1 3 3 (2x 1) 2 (2x 1) (2x 1 1 : ) 2x Çözüm 2 2 2 2 2 2 2 2 25 3 (2x 1) 6 25 2x 1 3 (2x 1) 19 2x 1 her iki taraf tan 6 çıkaralım 3 (2x 1) 6 13 2x 1 3 2x 1 13 2x 1 3 2x 1 13 2x 1 3 2x 13 1 buluruz. 2x 1 75
3 3 9 x 3 x 54 olduğuna göre, x ifadesinin değeri kaçtır? x A) 29 B) 27 C) 25 D) 17 E) 15 www.matematikkolay.net 2 2 2 2 9 x 9 x 3 3 x 9 3x x x x 3x 9 0 dır. Her tarafı x 3 ile çarpalım. (x 3) : (x 3 Çözüm 3 3 3 3 x 9) 0 olur. x 27 0 x 27 dir. Buna göre; 54 54 x 27 27 2 25 buluruz. x 27 90
a a 3 olduğuna göre, 4a a a 1 ifadesinin sonucu kaçtır? A) 10 B) 12 C) 13 D) 15 E) 16 www.matematikkolay.net 2 2 2 a a 3 (I.eşitlik) a 3 a kare alalım. a 6a 9 a a 7a 9 0 a 7a 9 dur. (IIeşi : . Çözüm 2 2 2 9 tlik) 4a a a 1 i bulalım. 4a a a 3 1 ( a a 3 idi. ) 4a a 3a 1 a 7a 1 (a 7a 9) 10 buluruz. 113
2 2 a ve b gerçel sayılar olmak üzere, a b 10 ve 2a 6b sayılarının aritmetik ortalaması geometri 2 k ortalamasına eşit ise, a b kaçtır? www.matematikkolay.net 2 2 2 2 2 2 2 2 2 2 2 2 a b 10 2a 6b (a b 10)( 2a 6b), 2 a 2a 1 b 6b 9 (a b 10)( 2a 6b) 2 (a 1) (b 3) (a b 2 : Çözüm 2 2 2 2 2 2 2 2 2 2 2 2 10)( 2a 6b) (a 1) (b 3) (a 1) 2a (b 3) 6b ( 2a 6b) 2 x (a 1) (b 3) ve y 2a 6b olsun. x (x y)( y) olur. 2 x 4(x y)( y) x 4xy 4y x 4xy 4y 0 (x 2y) 0 x 2y dir. a ve b olarak yerine yazalım 2 2 2 2 2 2 2 . a 2a 1 b 6b 9 4a 12b a 2a 1 b 6b 9 0 (a 1) (b 3) 0 a 1 ve b 3 buluruz. Buna göre; a b 1 3 2 buluruz. 143
3 2 2 2 x 1 olmak üzere x 2x 8x 5 0 25 olduğuna göre, x işleminin sonucu kaçtır? x A) 19 B) 21 C) 23 D) 2 5 E) 27 3 2 3 2 2 5x x 6 1 3 x 2x 8x 5 0 ifadesini x 3x 3x 1 5x 11x 6 0 şeklinde yazabiliriz. x 1 x 1 5 0 : x 6 Çözüm 2 2 2 0 2 2 2 2 2 x 1 x 1 5x 6 0 x 1 x 2x 1 5x 6 0 x 1 x 3x 5 0 x 3x 5 0 her tarafı x ‘e bölelim. 5 x 3 0 x 5 x 3 kare alalım. x 25 x 10 9 x 25 x 19 buluruz. x www.matematikkolay.net 171
www.matematikkolay.net 5 2 2 a a 1 ifadesinin çarpanlarından biri aşağıdaki – lerden hangisidir? A) a 1 B) a a 1 C) a a 1 3 2 3 2 D) a a 1 E) a a 1 5 2 5 2 2 2 3 2 a a 1 ifadeye a ekleyip çıkarınca bir sonuç elde ediliyor. a a a a 1 a 1 a : a Çözüm 2 2 2 2 2 2 3 2 a 1 a a 1 a a 1 a a 1 a a 1 a a 1 1 a a 1 a a 1 elde ederiz. Cevap: E 181
1 1 olduğuna göre, a 1 b 2 a 1 . b 2 ifadesinin değeri kaçtır? a 3 . b 2 a 1 .b tır? 1 1 1 1 A) B) C) D) 4 6 8 1 E) 10 12 www.matematikkolay.net b 2 a 1 1 1 a 1 b 2 4 4 a 1 b 2 a 1 b 2 a b 1 a 1 b 2 : Çözüm 4 a b 1 4k , a 1 b 2 k olsun. Bunları kullanacağız. a 1 b 2 a 3 b 2 a 1 b a 1 b 2 a 1 2 b 2 a 1 b 2 2 a 1 b 2 a 1 b 2 2b 4 a 1 (b 2) 2a 2 a 1 b 2 2 a 1 b 2 2a 2b 2 a 1 b 2 2 a 1 b 2 2 a b 1 k k 1 buluru 2.k 2.4k 10k 10 z. 183
2 2 a gerçel sayısı için, 20a 2 a 1 14a olduğuna göre, kaçtır? a 1 A) 1 B) 2 C) 2 D) 3 E) 4 www.matematikkolay.net 2 2 4 2 2 4 2 2 4 20a 2 iki tarafın karesini alalım. a 1 400a 2 a 2a 1 400a 2a 4a 2 396a 2a 2 : Çözüm 2 4 2 2 4 2 2 2 2 2 2 2’ye bölelim. 198a a 1 iki taraf tan da 2a çıkaralım. 196a a 2a 1 14a a 1 olur. 14a a 1 diyebiliriz. 14a 1 buluruz. a 1 203
www.matematikkolay.net 2 1 x 4 x 1 ise x ? x 1 2 2 3x 3 2 x 4 x 2x 1 3x 3 x tir. Bu cepte 1 x x 1 3x 3 : x 1 4x 4 x 4 tür. x 1 x 1 x 1 x 1 Çözüm 223


çoooooooooooook zor hiçbirini çözemedim
7.soruyu neden o kadar zorlaştırdınız ki iki sayının aritmetik ortalaması ile geometrik ortalaması eşit olunca sayılar birbirine eşit olmuyor mu ?a^2+b^2+10=-2a-6b yapıp hepsini aynı tarafta toplarsak sonuç yine (a+1)^2+(b+3)^2=0 çıkıyor
Uyarınız için teşekkürler. Eşit olduklarını kanıtlayarak gitmişiz, biraz gereksiz olmuş. Şimdi çözüm yenilendi.