Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Ortak paranteze alma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU

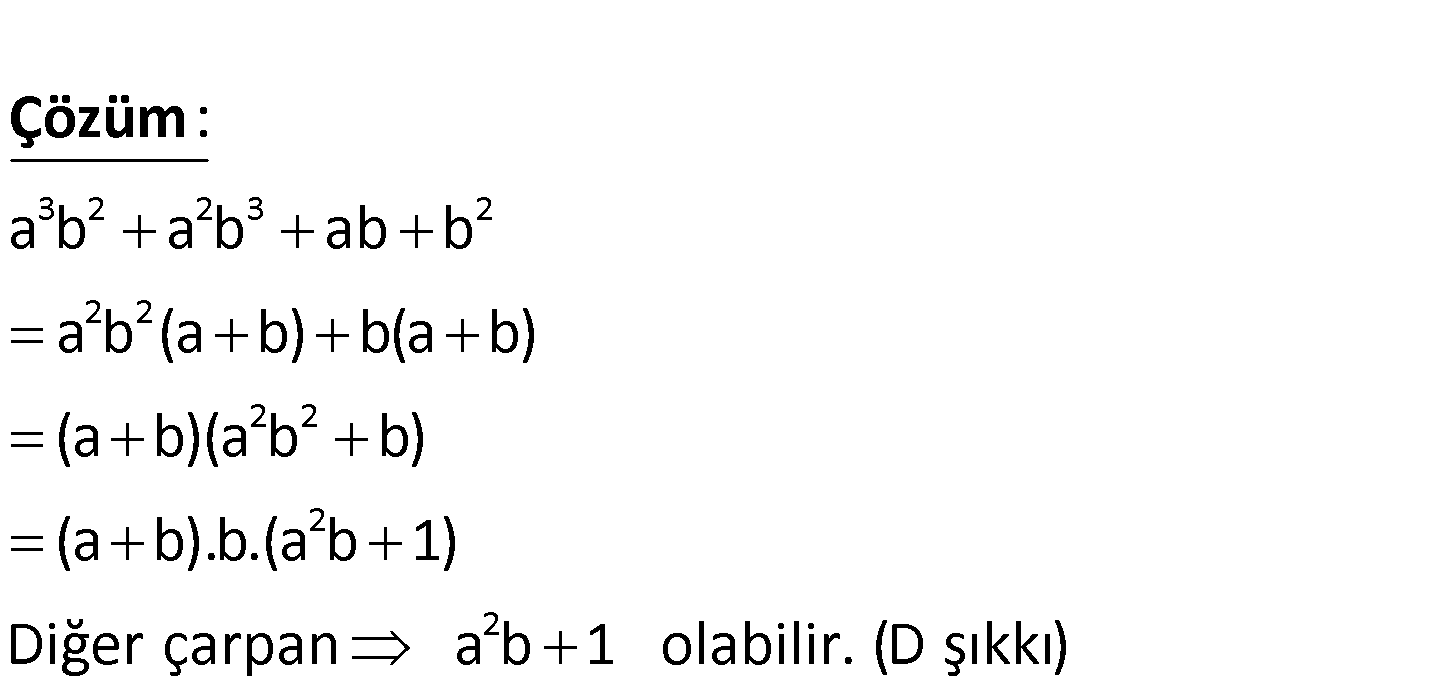
4.SORU
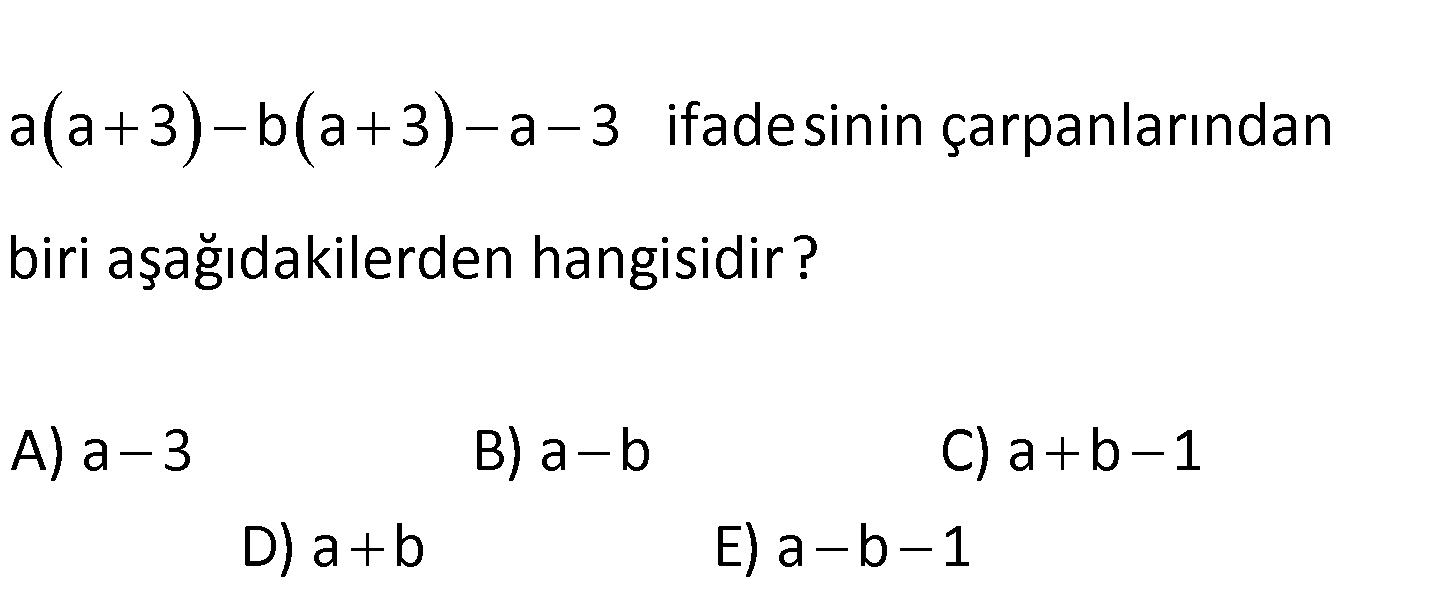

5.SORU


6.SORU


7.SORU


8.SORU

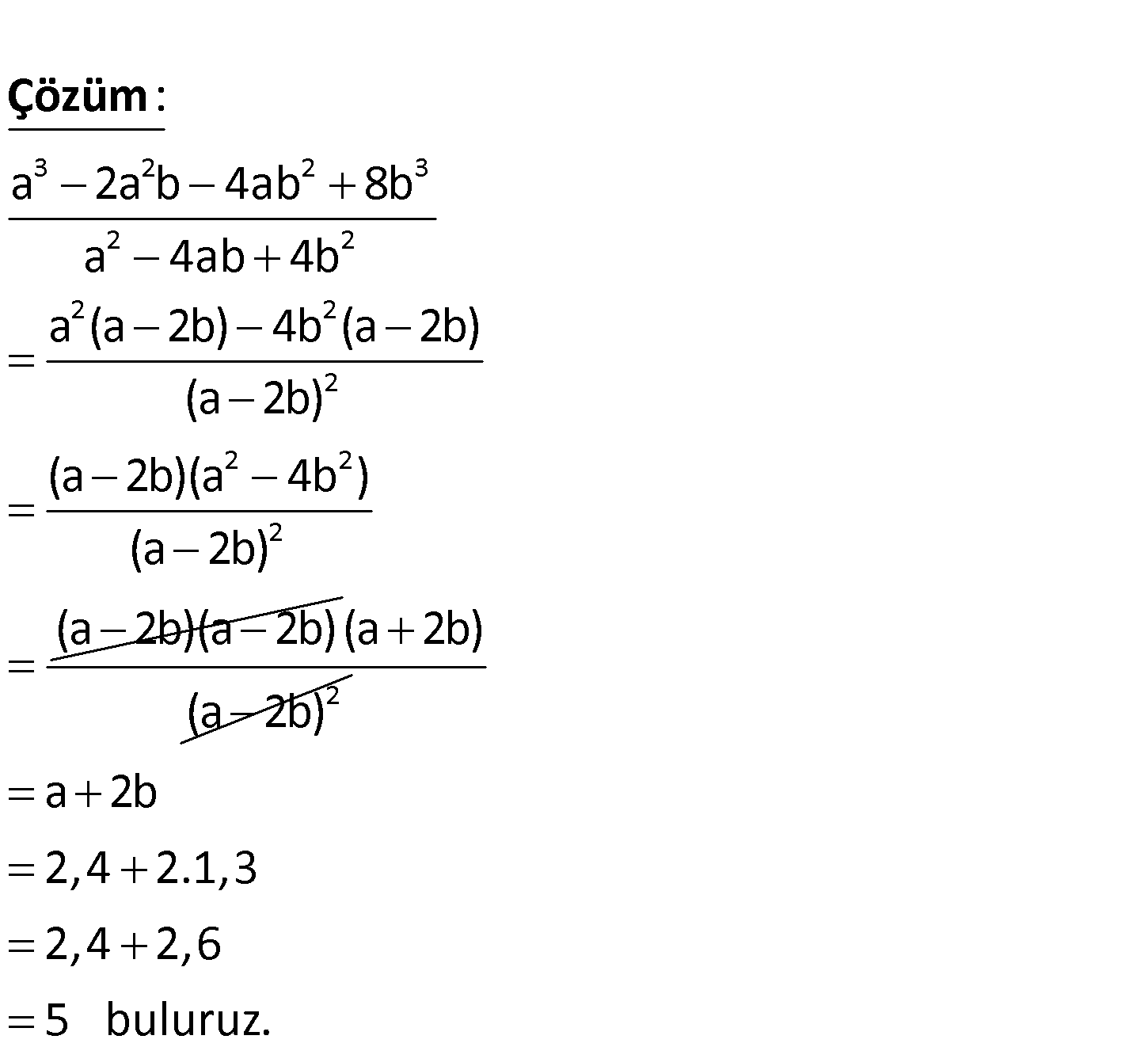
9.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 3 2 2 2 2 x a a x a : x 2ax a (ax a ) ifadesinin sadeleştirilmiş biçimi aşağıdakilerden hangisidir? A) a x a x a 1 B) a C) D) E) x a x a a www.matematikkolay.net 2 3 2 2 2 2 2 2 2 2 2 x a a x a İkinci kesri çarpım şeklinde : x 2ax a (ax a ) yazalım x a (ax a ) x 2ax a a x : Çözüm 3 2 2 2 2 2 2 2 a x a a(x a) (x a) a (x a) x a a (x a) (x a) a (x a) x a 2 (x a) 2:00 AM 2 (x a) 2 a (x a) 1 buluruz. 8
x y 2 ve a 5 2b eşitlikleri veriliyor. Buna göre, 3ax 3ay 6bx 6by ifadesinin değeri kaçtır? A) 30 B ) 10 C) 6 D) 10 E) 30 www.matematikkolay.net 2 x y 2 x y 2 a 5 2b a 2b 5 tir. 3ax 3ay 6bx 6by 3a(x y : ) 6b(x y) (x y)(3a 6b) 6a 12b 6( Çözüm 5 a 2b) 30 buluruz. 63
3 2 2 3 2 a b a b ab b ifadesinin çarpanlarından biri a b olduğuna göre, diğer çarpanlardan biri aşağıdakil 2 2 erden hangisidir? A) a B) ab C) ab 1 D) a b+1 E) ab 3 2 2 3 2 2 2 2 2 2 2 a b a b ab b a b (a b) b(a b) (a b)(a b b) (a b).b.(a b 1) Diğer çarpan a b 1 olab : Çözüm ilir. (D şıkkı) www.matematikkolay.net 64
www.matematikkolay.net a a 3 b a 3 a 3 ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) a 3 B) a b C) a b 1 D) ab E) ab 1 2 2 a.(a 3) b.(a 3) a 3 a 3a ba 3b a 3 a 2a 3 ba 3b (a 3)(a 1) b(a 3) (a 3)(a 1 b) dir. : Çözüm E şıkkındaki (a b 1) ifadesinin, çarpanlardan biri olduğunu görüyoruz. 74
2 2 a 2b 4 b c 5 eşitliği veriliyor. Buna göre, a 2b 3ab ac 2bc işleminin sonu – cu kaçtır? A) 4 B) 1 C ) 9 D) 16 E) 20 www.matematikkolay.net 2 2 4 a 2b 3ab ac 2bc a(a 3b c) 2b(b c) a(a 2b b c) 2b(b c) a(4 b c) 2b(b c) 4a a(b c) 2b(b c) : Çözüm 4 4 5 4a (b c)(a 2b) 4a 4b 4c 4(a b c) 4(a 2b c b) 4.( 1) 4 buluruz. 62
3 2 2 2 x 6x 11x 6 5 olduğuna göre, x 5x 6 x 5x 1 ifadesinin değeri kaçtır? A) 5 B) 6 C) 7 D) 8 E) 9 3 2 2 3 2 2 2 x 6x 11x 6 5 x 5x 6 (Pay kısmını paydaya benzetmek için parçalayalım) x 5x x 6x 5x 6 x 5 : Çözüm 2 2 2 2 5 x 6 x(x 5x 6) (x 5x 6) 5 x 5x 6 (x 5x 6) 2 (x 1) x 5x 6 2 2 5 x 1 5 x 6 dır. x 5x 1 6 5.6 1 5 buluruz. 30
, 3 2 a 2 ve a a a 10 0 olduğuna göre, 5 a kaçtır? a A) 5 B) 4 C) 3 D) 0 E) 2 www.matematikkolay.net 3 2 3 2 iki küp (a 2)(a 1) farkı a a a 10 0 (10’u 2 ve 8 şeklinde yazalım) a 8 a a 2 0 a : ( Çözüm 2 2 2 2 2 2)(a 2a 4) (a 2)(a 1) 0 (a 2)(a 2a 4 a 1) 0 (a 2)(a 3a 5) 0 a 3a 5 0 a 5 3a (Her tarafı a’ ya bölelim) 5 a 3 buluruz. a 40
3 2 2 3 2 2 a 2,4 ve b 1,3 olduğuna göre, a 2a b 4ab 8b ifadesinin sonucu kaçtır? a 4ab 4b A) 5 B) 4,8 C) 4,6 D) 4 E) 3,5 www.matematikkolay.net 3 2 2 3 2 2 2 2 2 2 2 2 a 2a b 4ab 8b a 4ab 4b a (a 2b) 4b (a 2b) (a 2b) (a 2b)(a 4b ) (a 2b) (a 2 : b)(a 2b) Çözüm 2 (a 2b) (a 2b) a 2b 2,4 2.1,3 2,4 2,6 5 buluruz. 112
www.matematikkolay.net 3 2 2 m. m n . p m m p m . m n ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) m n B) m n C) 2m n D) 2mnp E) mn p 3 2 2 2 iki kare m. m n . p m m p m . m n İfadeyi ortak çarpanların parantezine alalım. m. m n . p m m n p m : Çözüm farkı m. mn . p m mnp m .m np m m. m n . p m 2m n p . n p Şıklarda bu 5 çarpandan 2m n p bulunuyor. 129


9. soruda p-m in küpü yazılmalı . karesi yazılmış
Uyarınız için teşekkürler. Soru düzeltildi.