Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında İki kare farkından yararlanarak soru çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
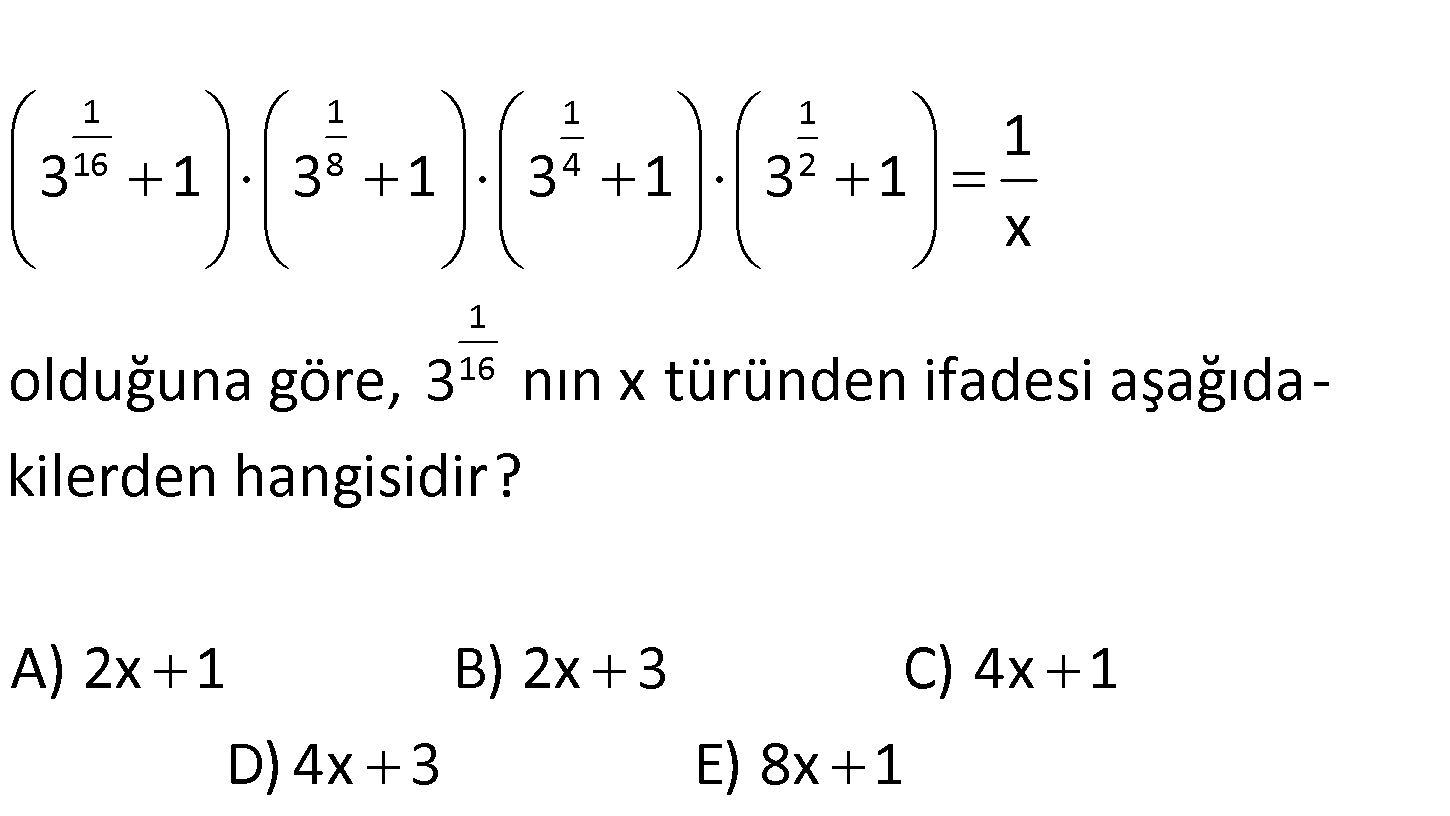
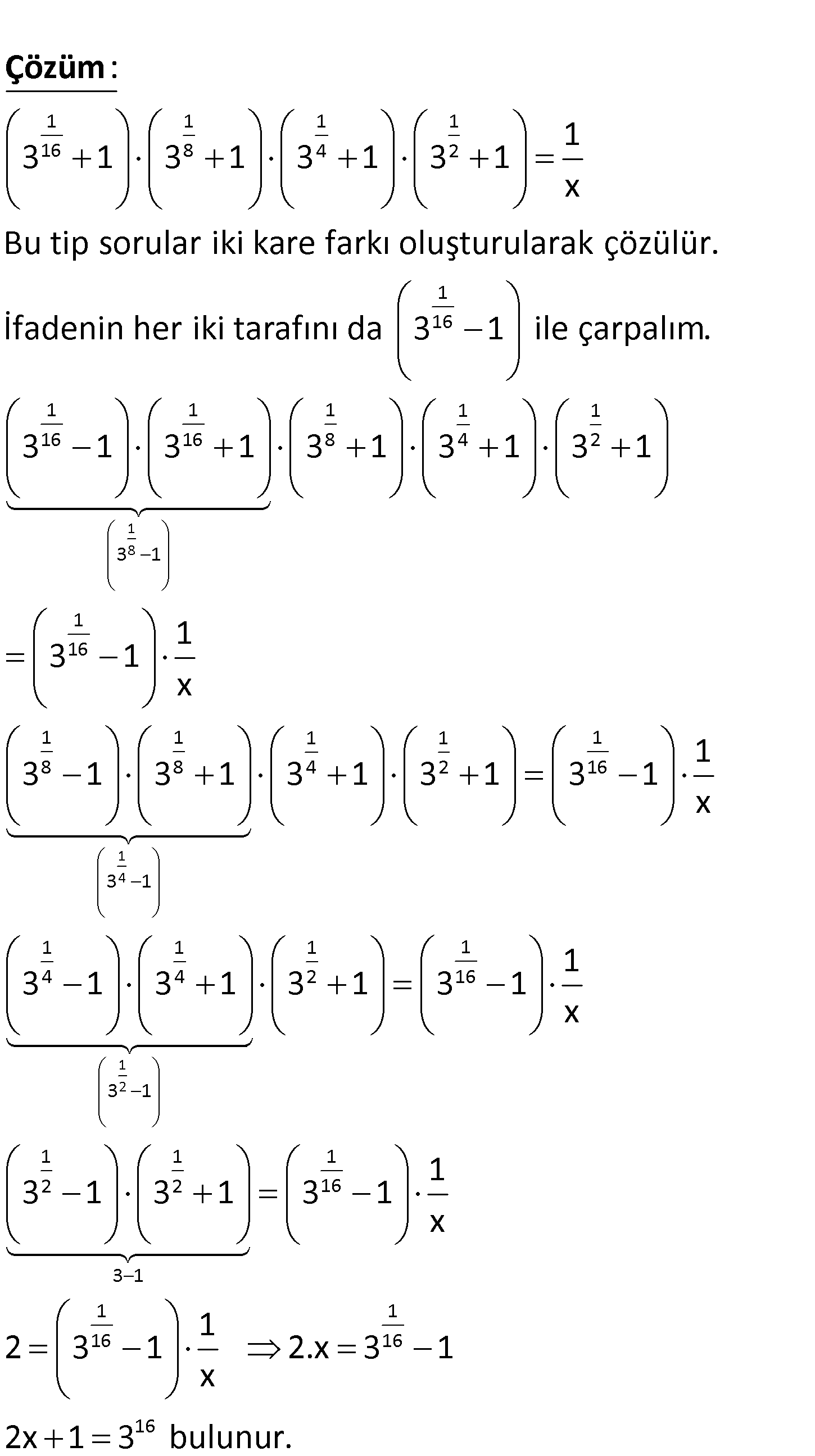
3.SORU
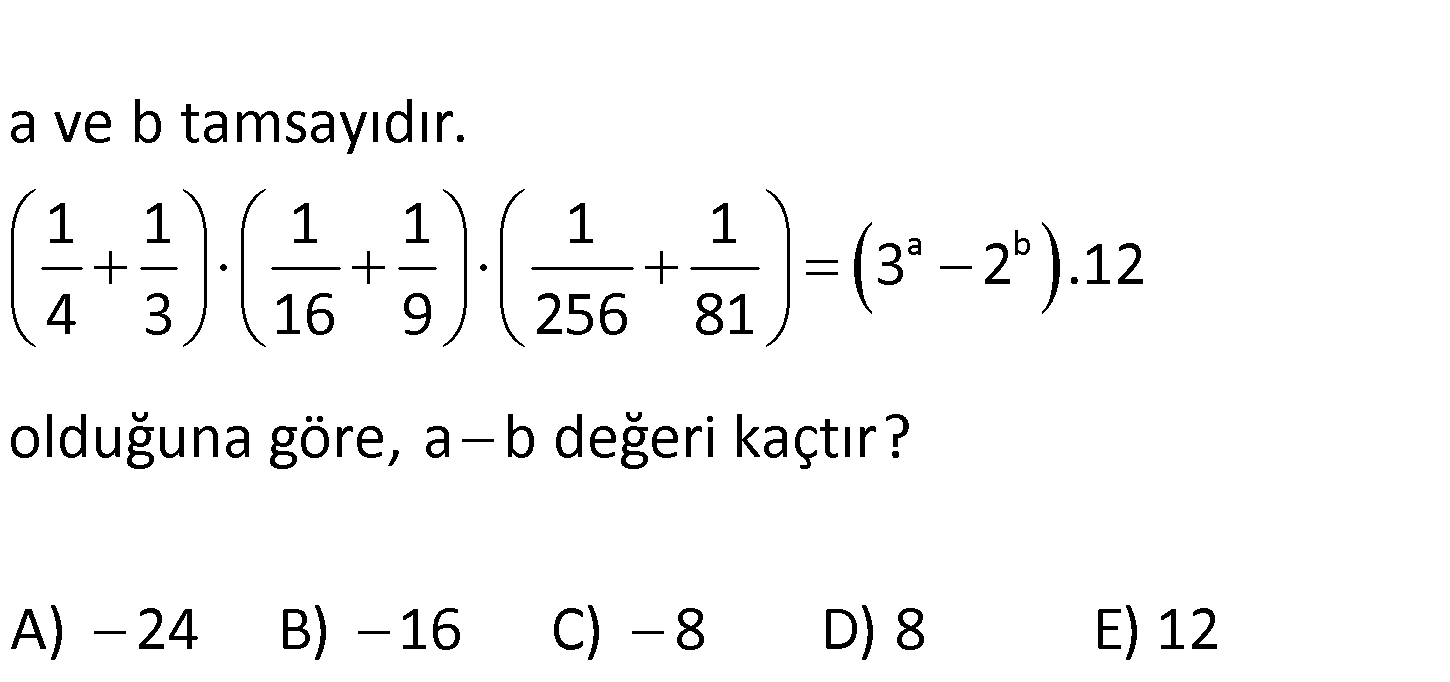
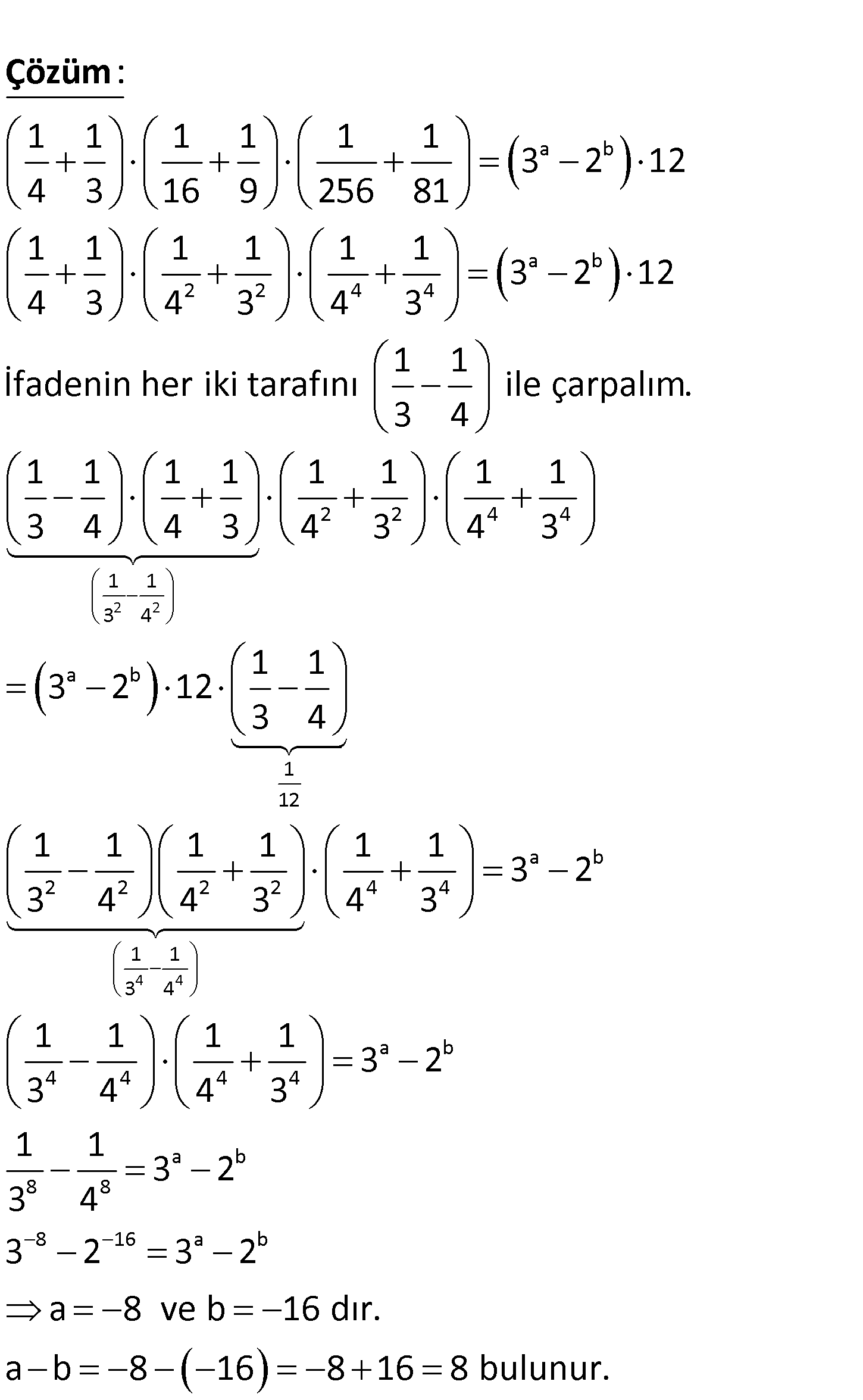
4.SORU
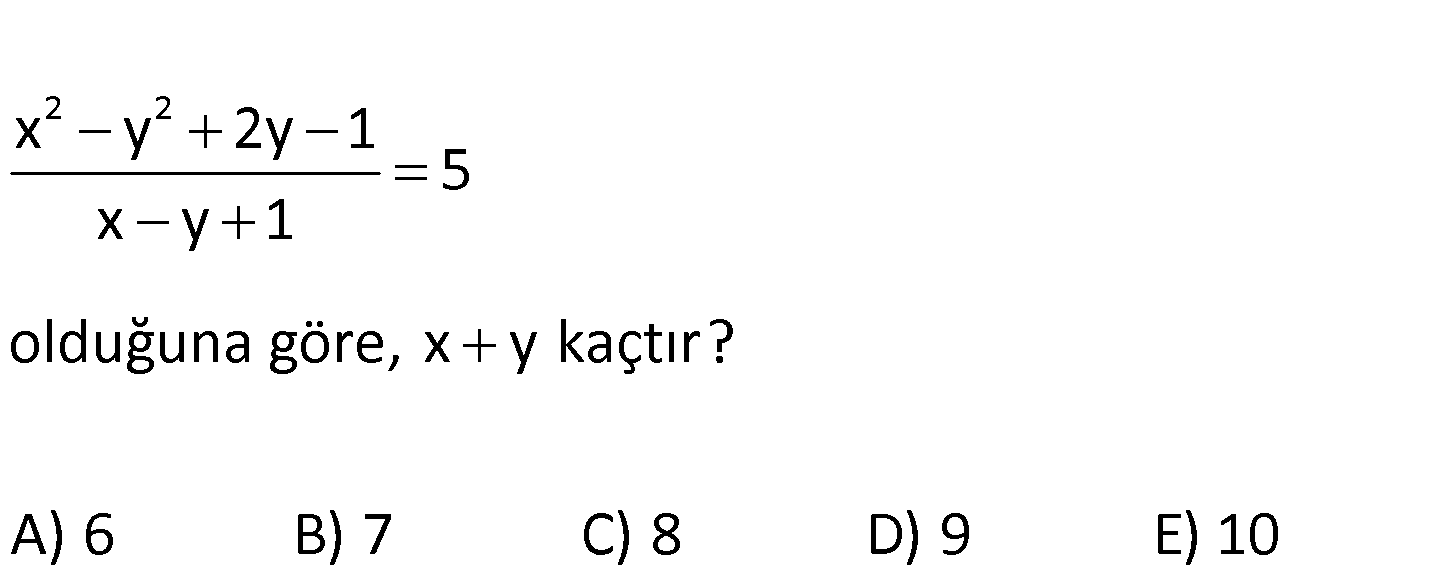

5.SORU
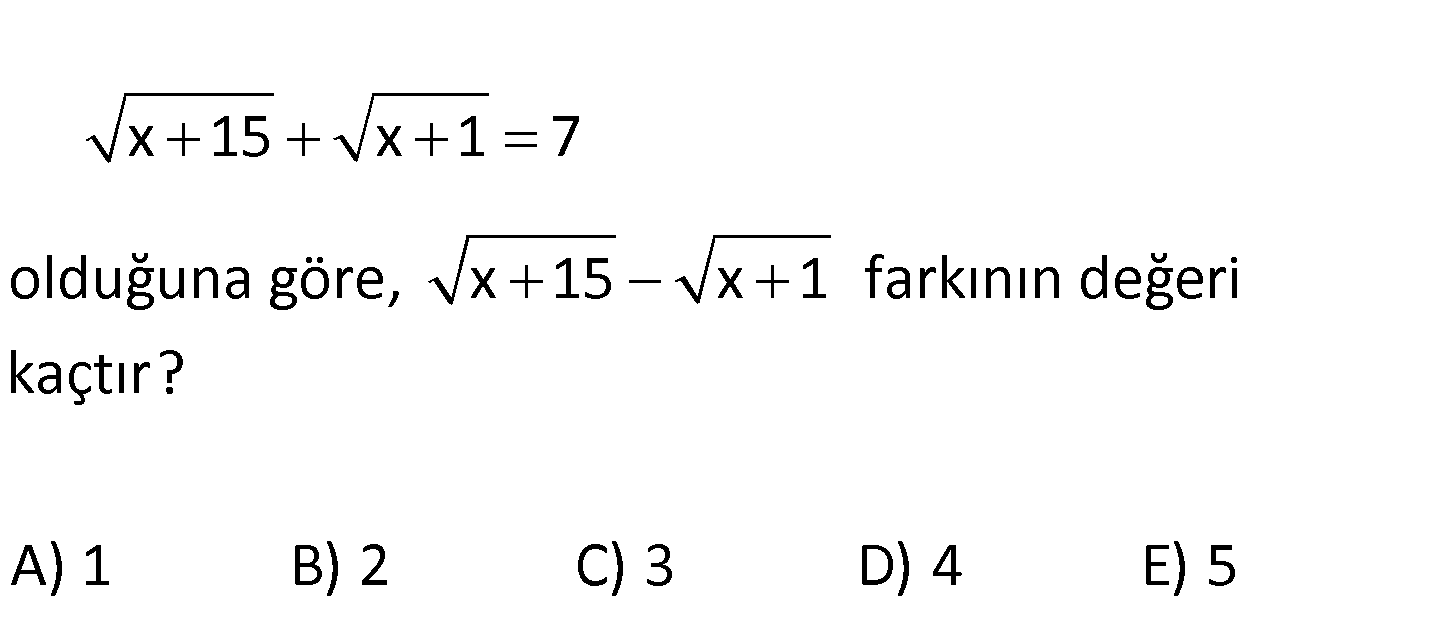

6.SORU
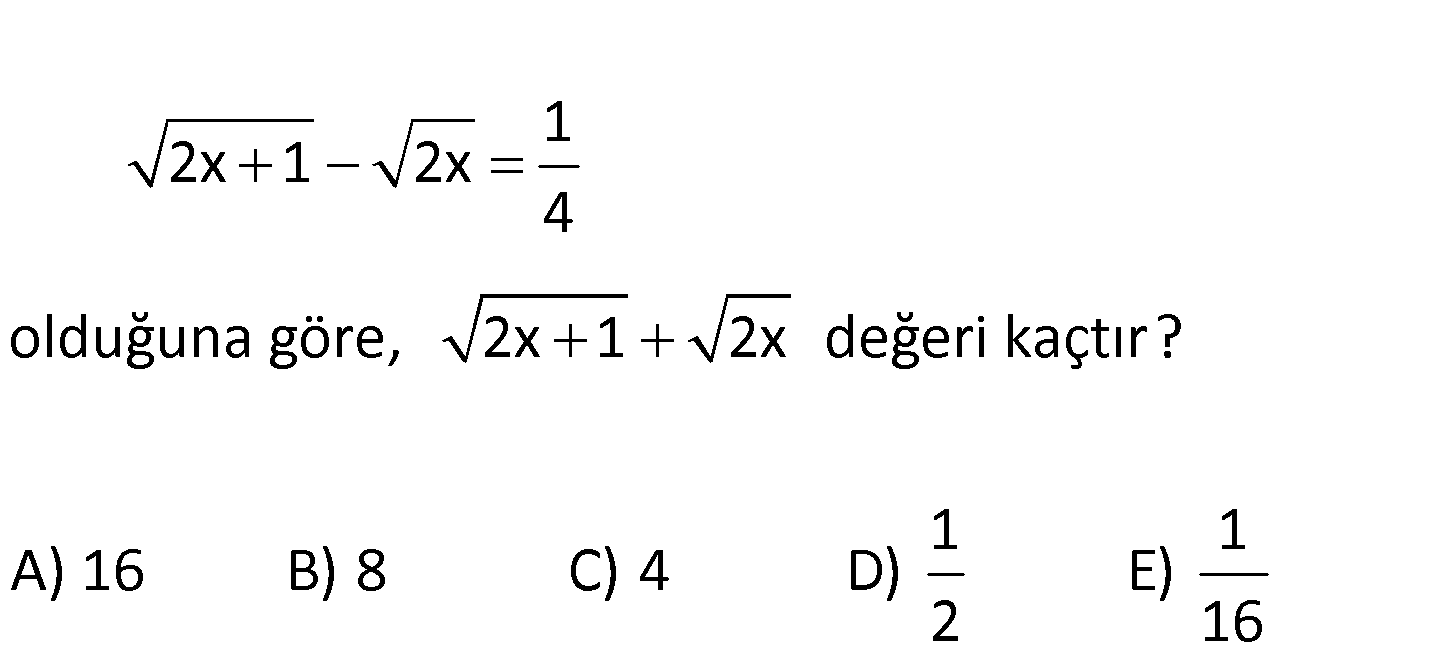

7.SORU
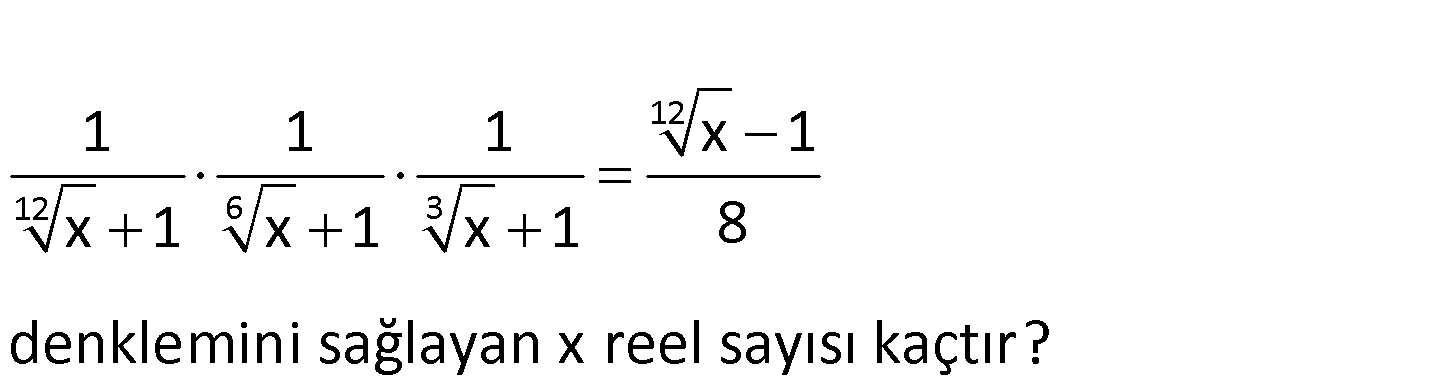
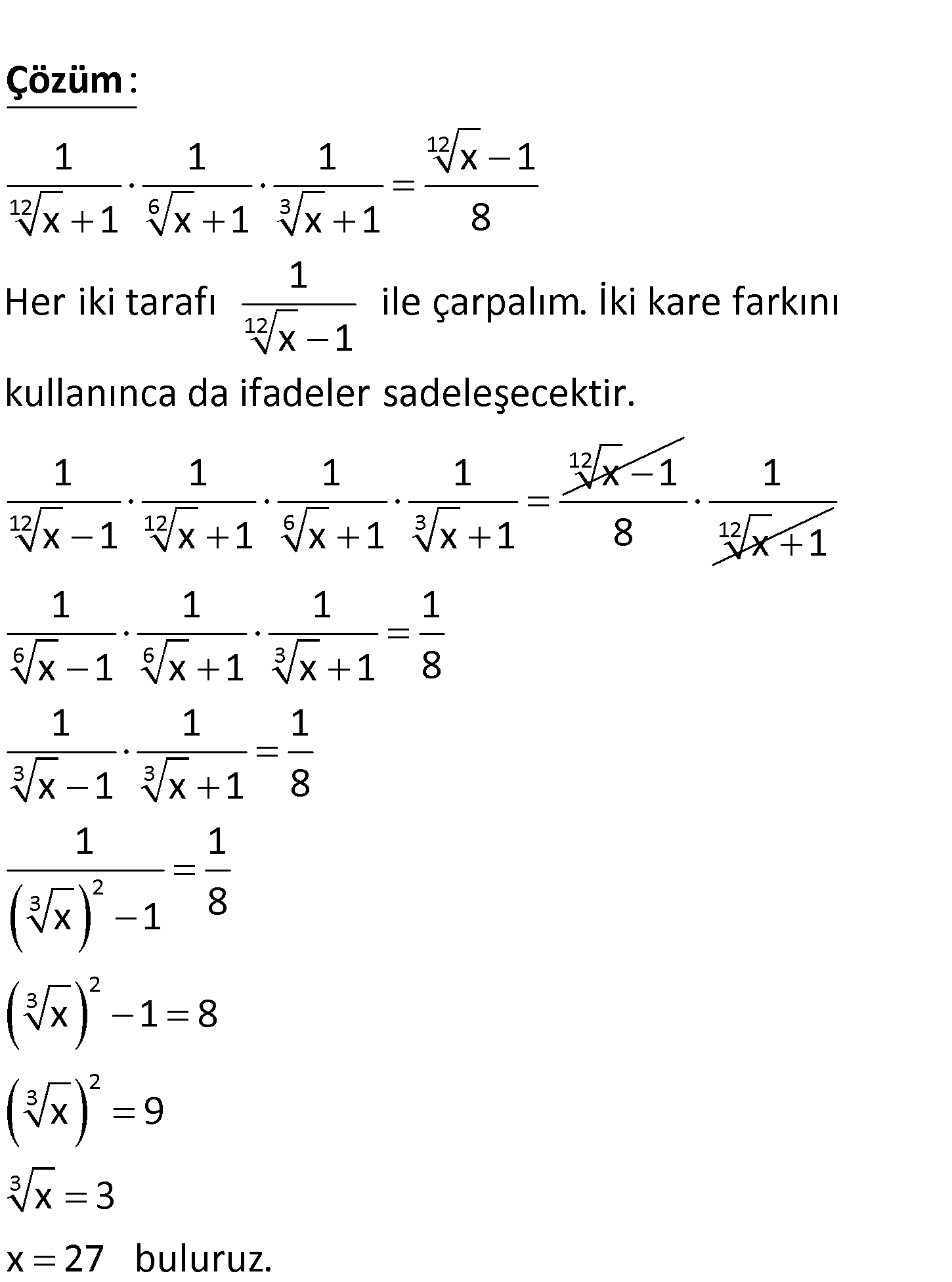
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
2 4 8 16 T 9 1 9 1 9 1 9 1 olduğuna göre, 9 sayısının T cinsinden eşiti aşağı – dakilerden hangisidir? A) 8T 1 B) 8T 1 C) 9T D)10T 1 E) 10T 1 2 2 4 8 2 9 1 9 T (9 1)(9 1)(9 1)(9 1) 9 1 ile her iki tarafı çarpalım. (9 1) T (9 1)(9 1 : )(9 1) Çözüm 4 8 16 4 8 1 9 1 9 1 16 16 (9 1)(9 1) 8T 9 1 8T 1 9 buluruz. www.matematikkolay.net 114
1 1 1 1 16 8 4 2 1 16 1 3 1 3 1 3 1 3 1 x olduğuna göre, 3 nın x türünden ifadesi aşağ ıda – kilerden hangisidir? A) 2x 1 B) 2x 3 C) 4x 1 D) 4x 3 E) 8x 1 www.matematikkolay.net 1 1 1 1 16 8 4 2 1 3 1 3 1 3 1 3 1 x Bu tip sorular iki kare farkı oluşturul : ar Çözüm 1 8 1 4 1 16 1 1 1 1 1 16 16 8 4 2 3 1 1 16 1 1 8 8 3 1 ak çözülür. İfadenin her iki tarafını da 3 1 ile çarpalım. 3 1 3 1 3 1 3 1 3 1 1 3 1 x 3 1 3 1 1 2 1 1 1 4 2 16 1 1 1 1 4 4 2 16 3 1 1 1 1 2 2 16 3 1 1 1 16 16 1 3 1 3 1 3 1 x 1 3 1 3 1 3 1 3 1 x 1 3 1 3 1 3 1 x 1 2 3 1 2.x 3 1 x 16 2x 1 3 bulunur. www.matematikkolay.net 115
a b a ve b tamsayıdır. 1 1 1 1 1 1 3 2 .12 4 3 16 9 256 81 olduğuna göre, a b değeri kaçtır ? A) 24 B) 16 C) 8 D) 8 E) 12 www.matematikkolay.net a b a 2 2 4 4 1 1 1 1 1 1 3 2 12 4 3 16 9 256 81 1 1 1 1 1 1 3 2 4 3 4 3 : 4 3 Çözüm 2 2 4 4 b 2 2 4 4 1 1 3 4 a b 1 12 2 2 2 2 1 1 3 4 12 1 1 İfadenin her iki tarafını ile çarpalım. 3 4 1 1 1 1 1 1 1 1 3 4 4 3 4 3 4 3 1 1 3 2 12 3 4 1 1 1 1 3 4 4 3 a b 4 4 a b 4 4 4 4 a b 8 8 8 16 a b 1 1 3 2 4 3 1 1 1 1 3 2 3 4 4 3 1 1 3 2 3 4 3 2 3 2 a 8 ve b 16 dır. a b 8 16 8 16 8 bulunur. 137
2 2 x y 2y 1 5 x y 1 olduğuna göre, x y kaçtır? A) 6 B) 7 C) 8 D) 9 E) 10 2 2 2 2 2 2 x y 2y 1 5 x y 1 x y 2y 1 5 x y 1 x y 1 5 x y 1 Pay kısmında iki kare farkını kullanalım. x : Çözüm y 1 x y 1 x y 1 5 x y 1 5 x y 5 1 6 bulunur. www.matematikkolay.net 146
x 15 x 1 7 olduğuna göre, x 15 x 1 farkının değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 x 15 x 1 y diyelim. Bunu soruda verilen ifade ile çarpalım. x 15 x 1 x 15 x 1 7y x 15 x 1 7y : 14 Çözüm 7y y 2 buluruz. www.matematikkolay.net 163
1 2x 1 2x 4 olduğuna göre, 2x 1 2x değeri kaçtır? 1 1 A) 16 B) 8 C) 4 D) E) 2 16 2 2 1 Eşitliği verilen ifade ile, sorulan ifadeyi çarpalım. İki kare farkı : a b a b a b 2x 1 2x : Çözüm y 4 2x 1 2x 2x 1 2x y 1 4 y 4 buluruz. 180
www.matematikkolay.net 12 12 6 3 1 1 1 x 1 x 1 x 1 x 1 8 denklemini sağlayan x reel sayısı kaçtır? 12 12 6 3 12 1 1 1 x 1 x 1 x 1 x 1 8 1 Her iki tarafı ile çarpalım. İki kare farkını x 1 : kullanınca da Çözüm 12 12 12 6 3 ifadeler sadeleşecektir. 1 1 1 1 x 1 x 1 x 1 x 1 x 1 12 1 8 x 1 6 6 3 3 3 2 3 2 3 2 3 3 1 1 1 1 x 1 x 1 x 1 8 1 1 1 x 1 x 1 8 1 1 x 1 8 x 1 8 x 9 x 3 x 27 buluruz. www.matematikkolay.net 226

