Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Basit çarpanlarına ayırma soruları, Kısa çarpanlarına ayırma soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
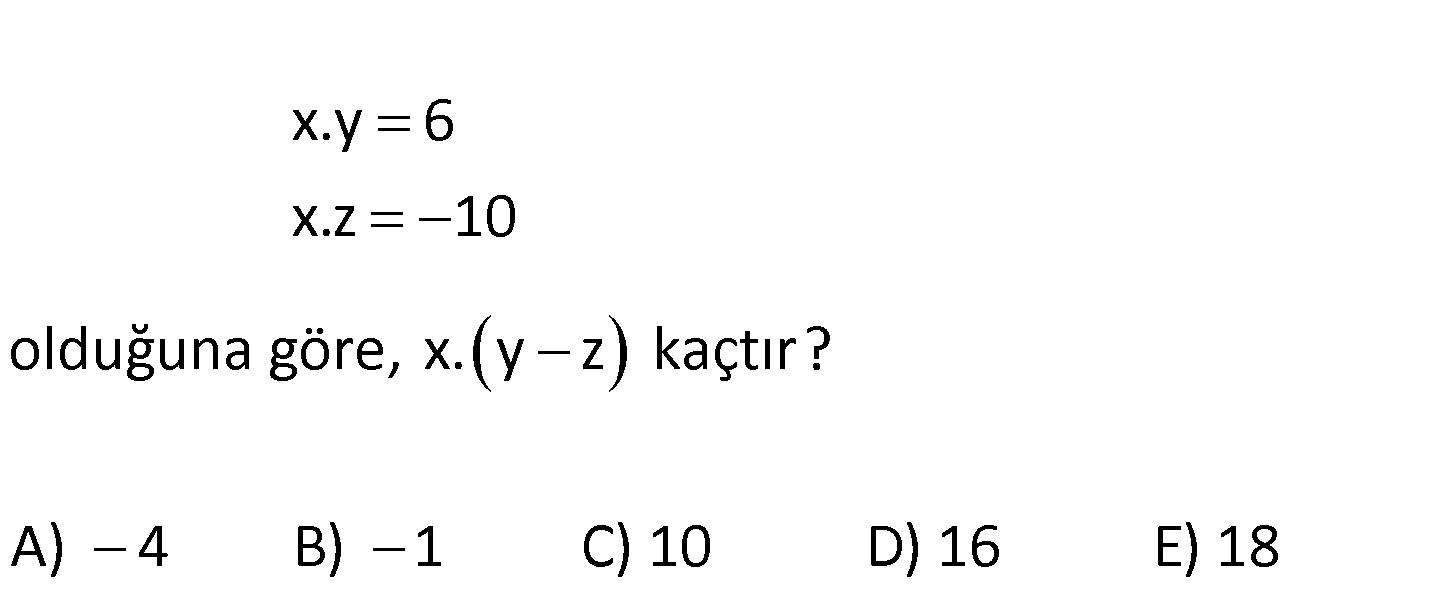

2.SORU

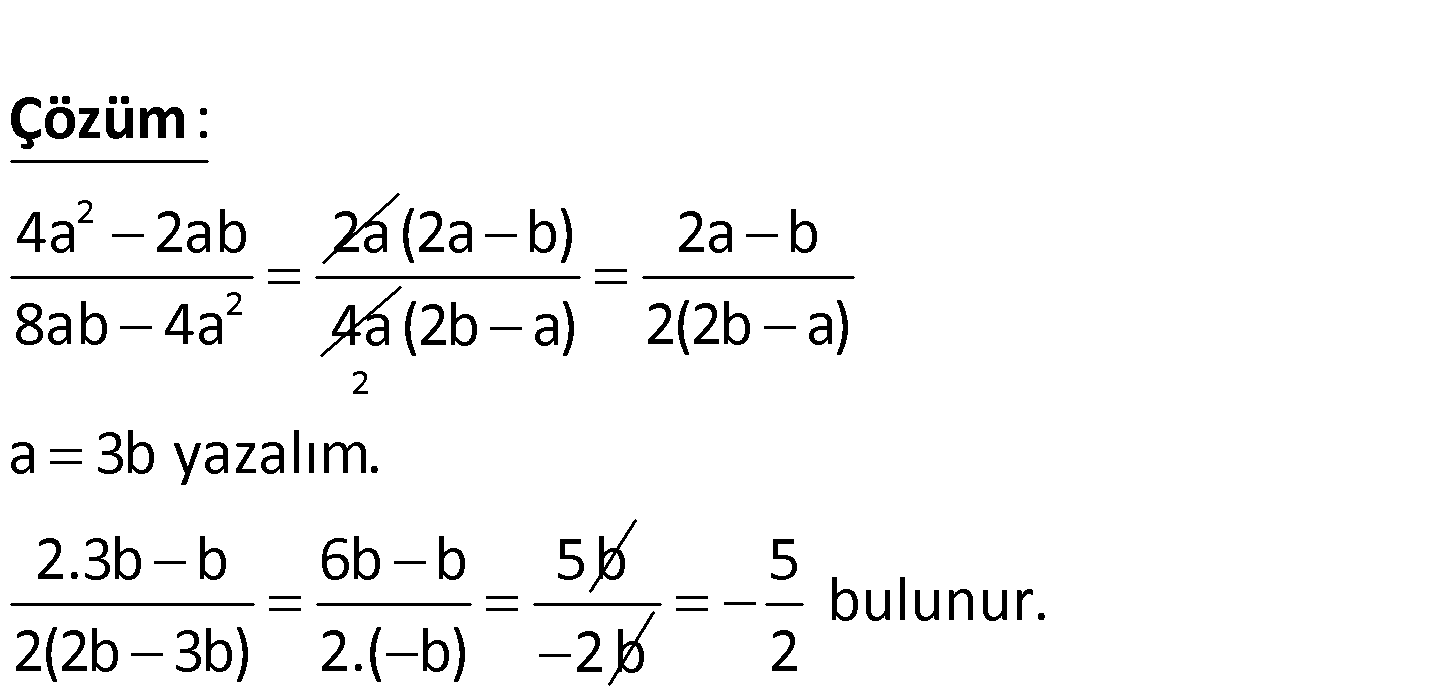
3.SORU
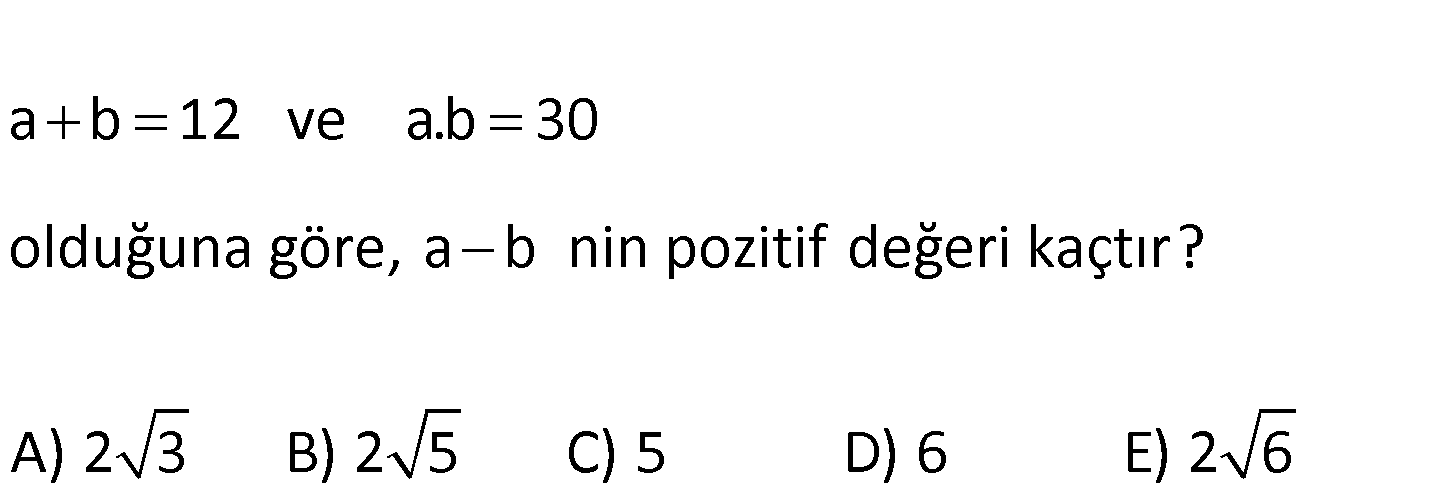

4.SORU


5.SORU
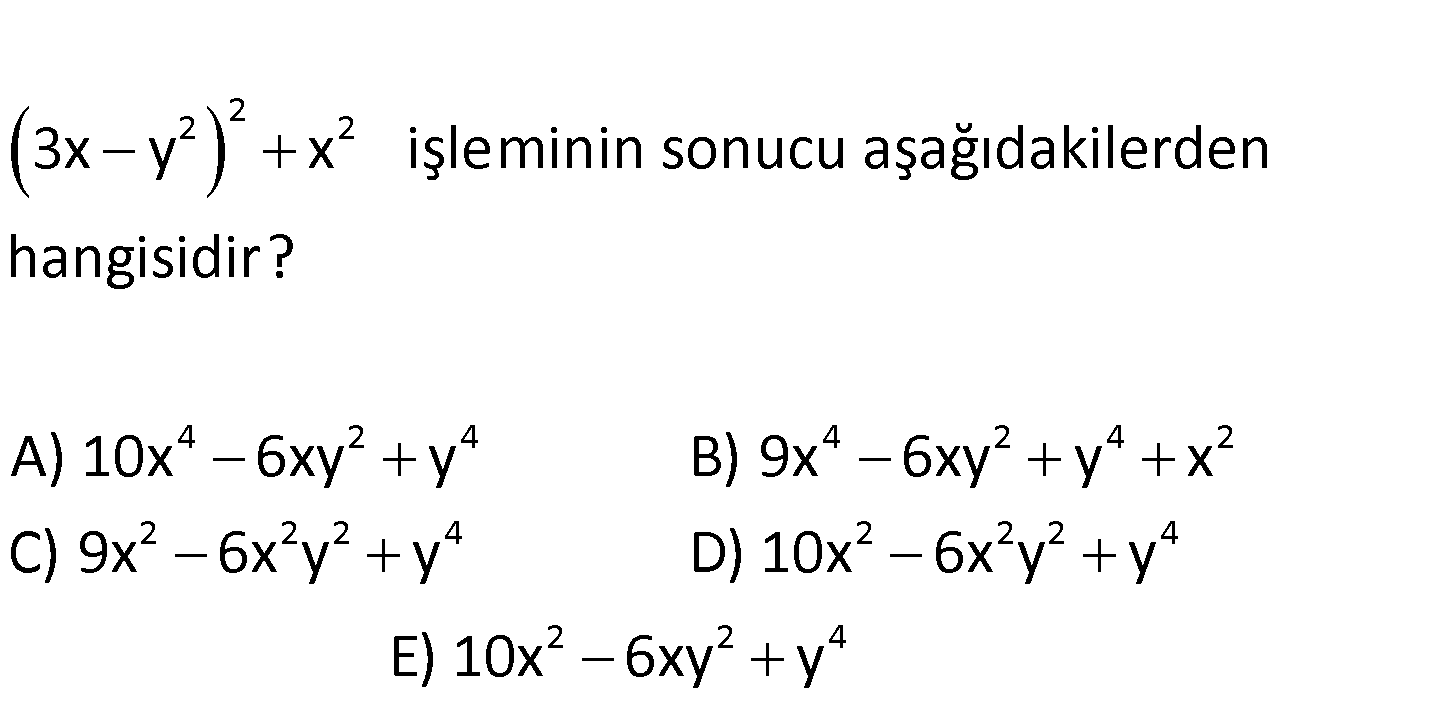

6.SORU
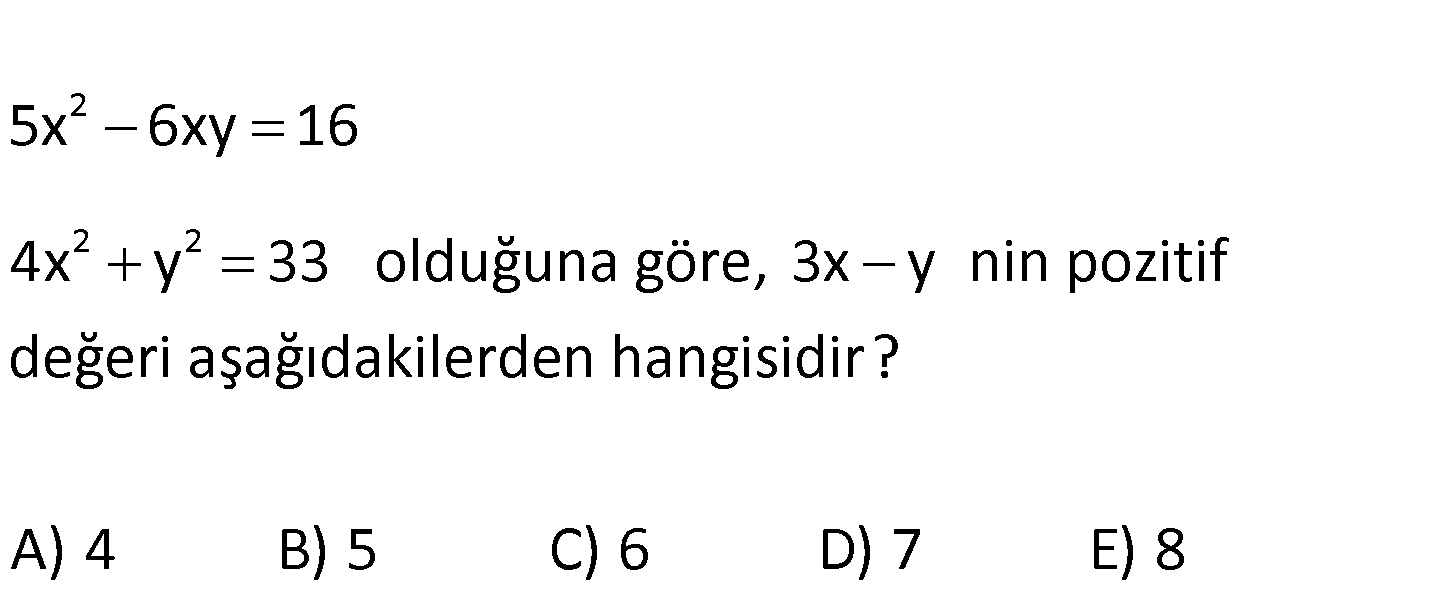

7.SORU


8.SORU

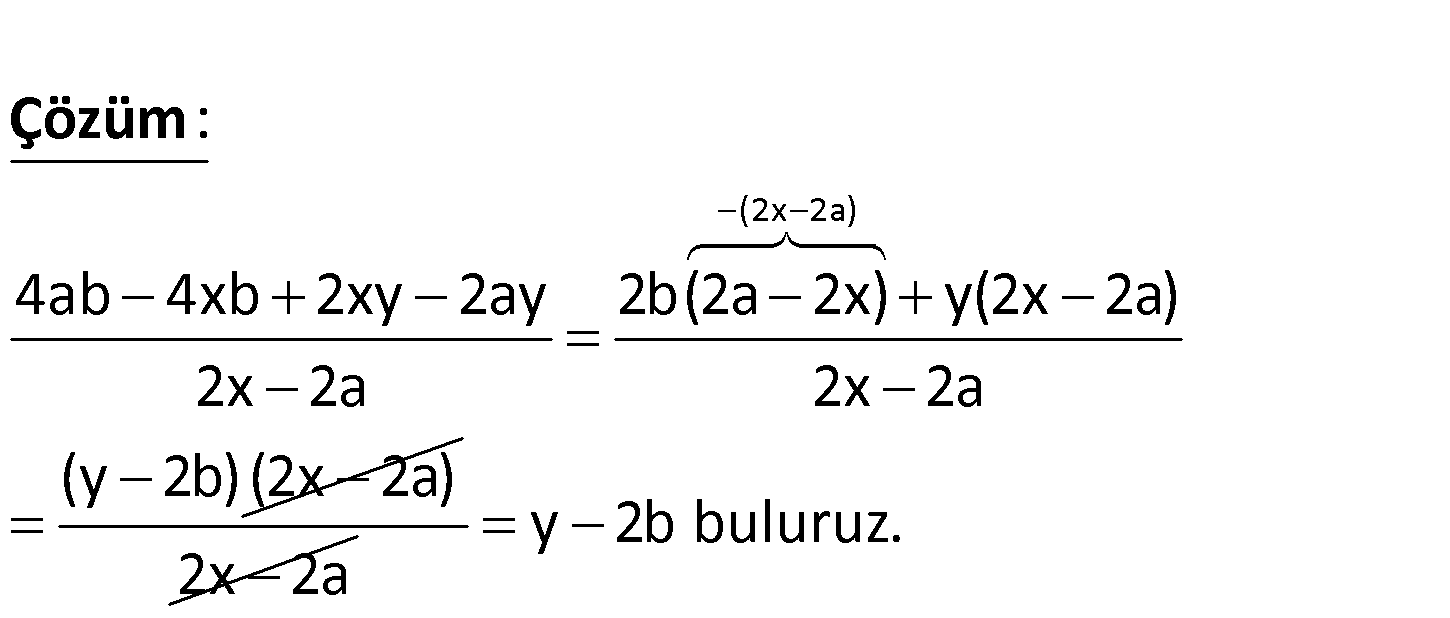
9.SORU
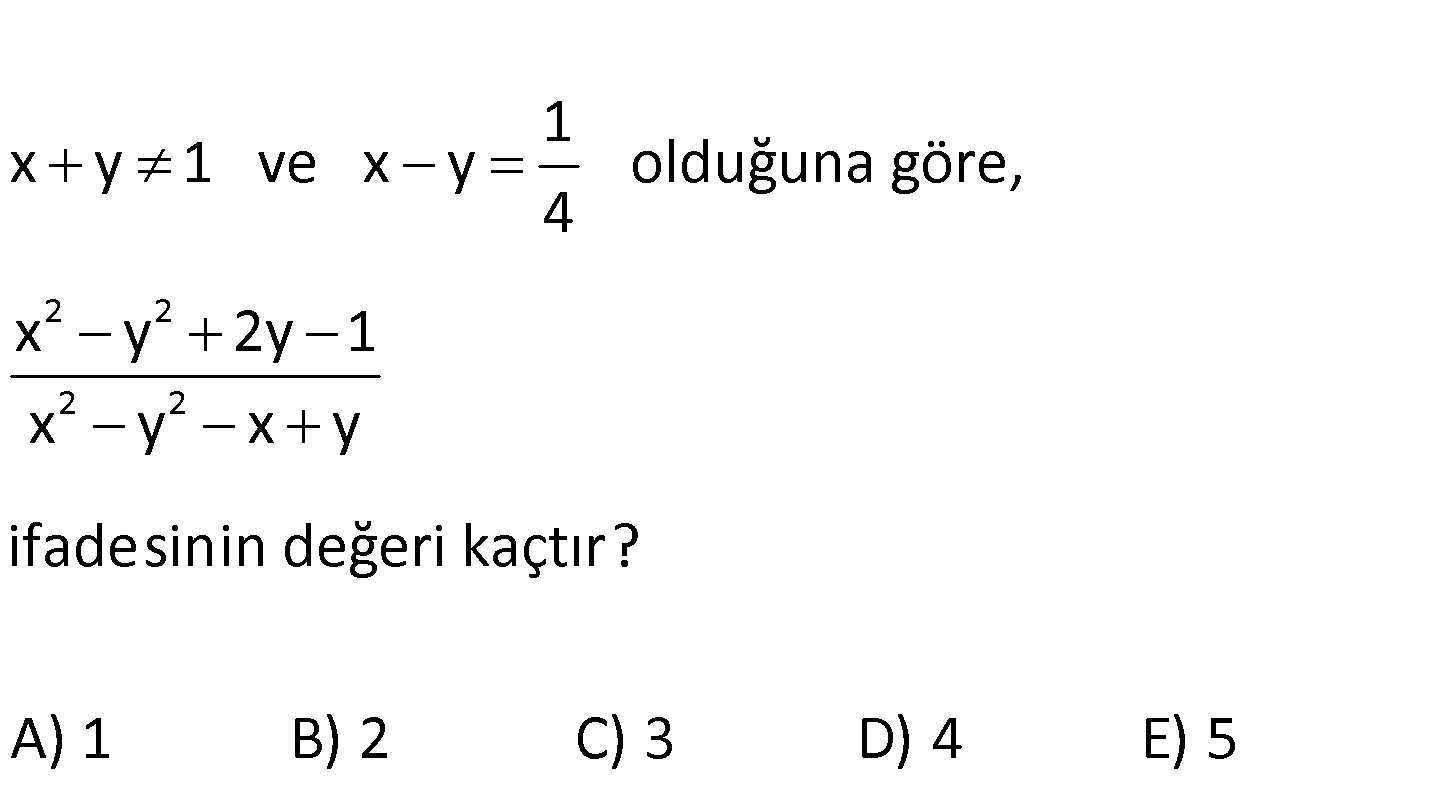
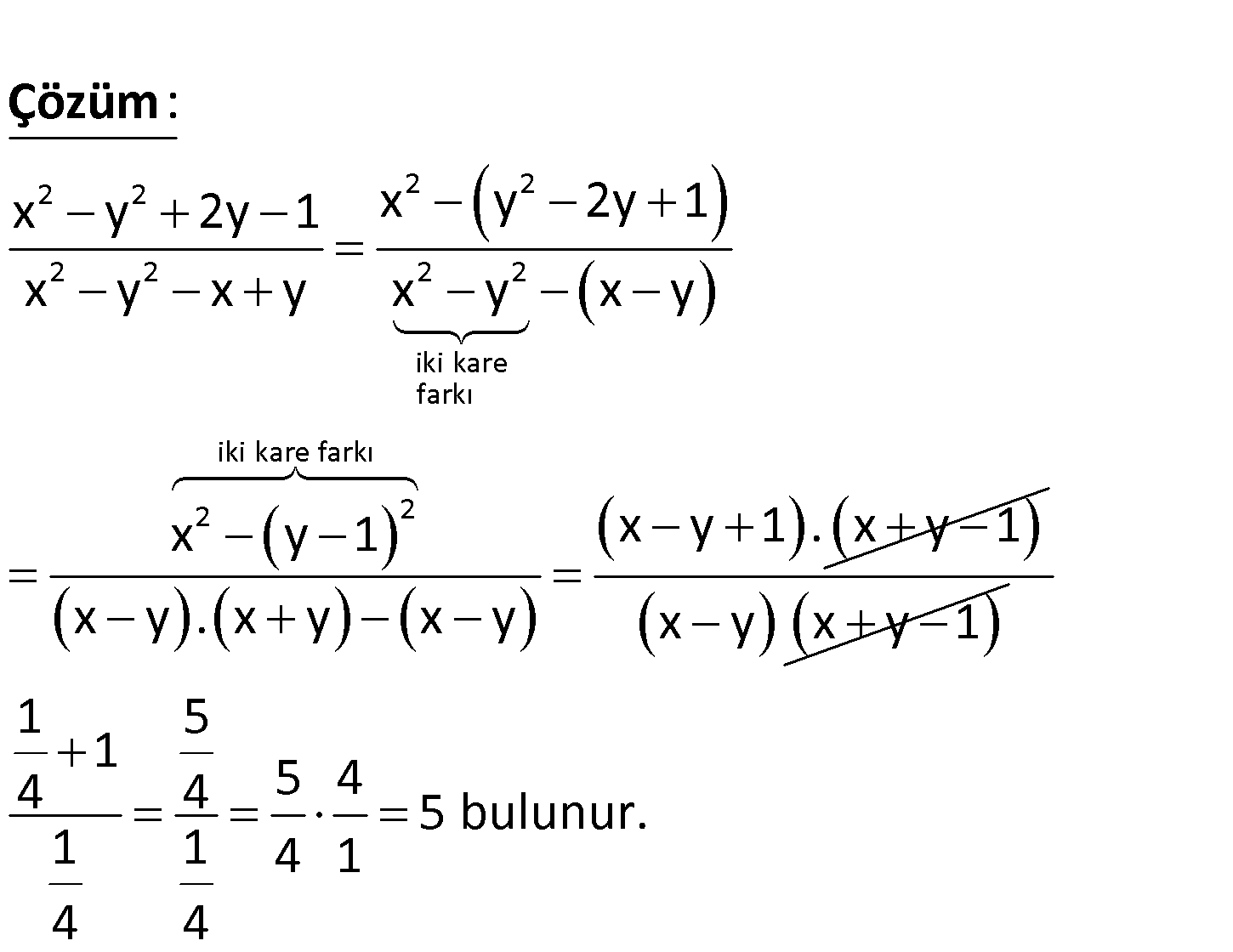
10.SORU
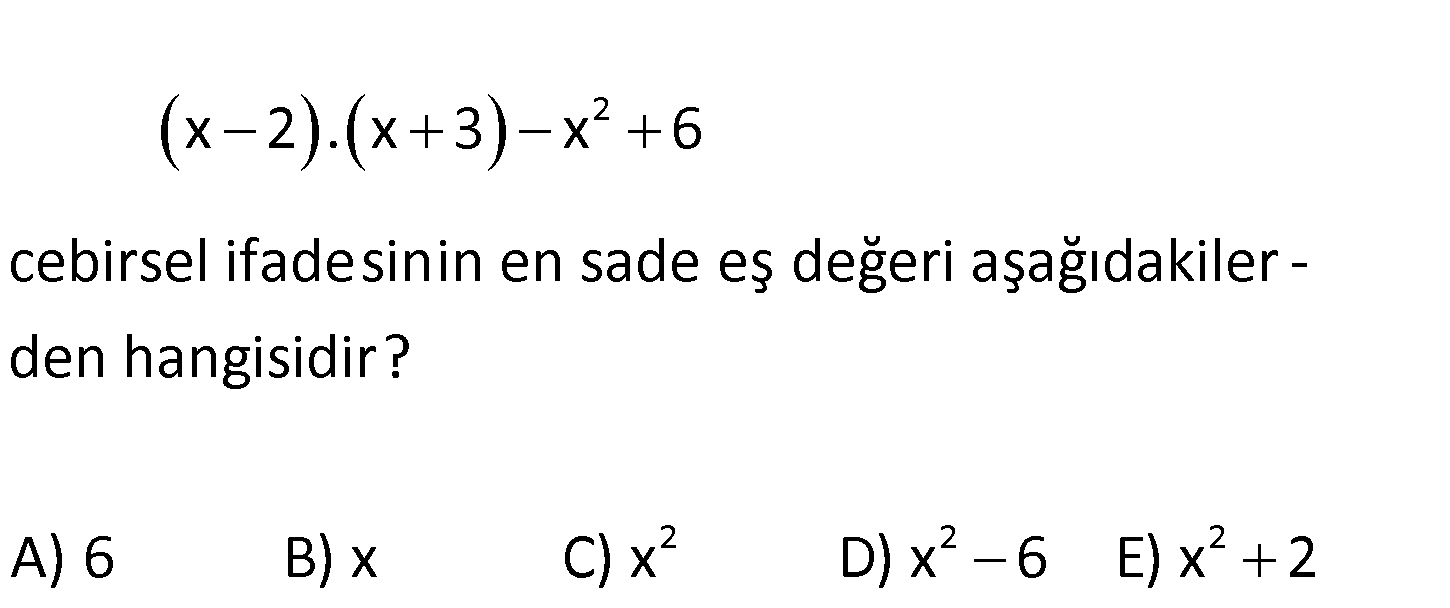
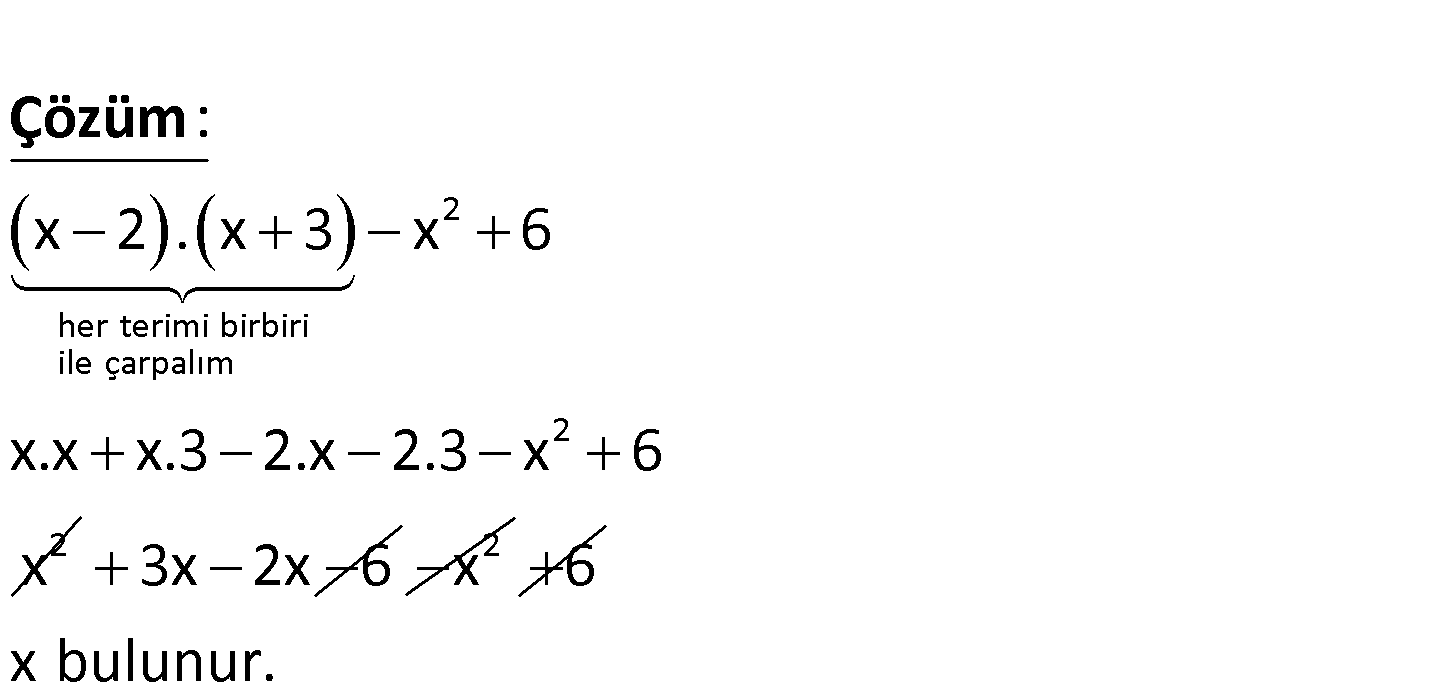
11.SORU
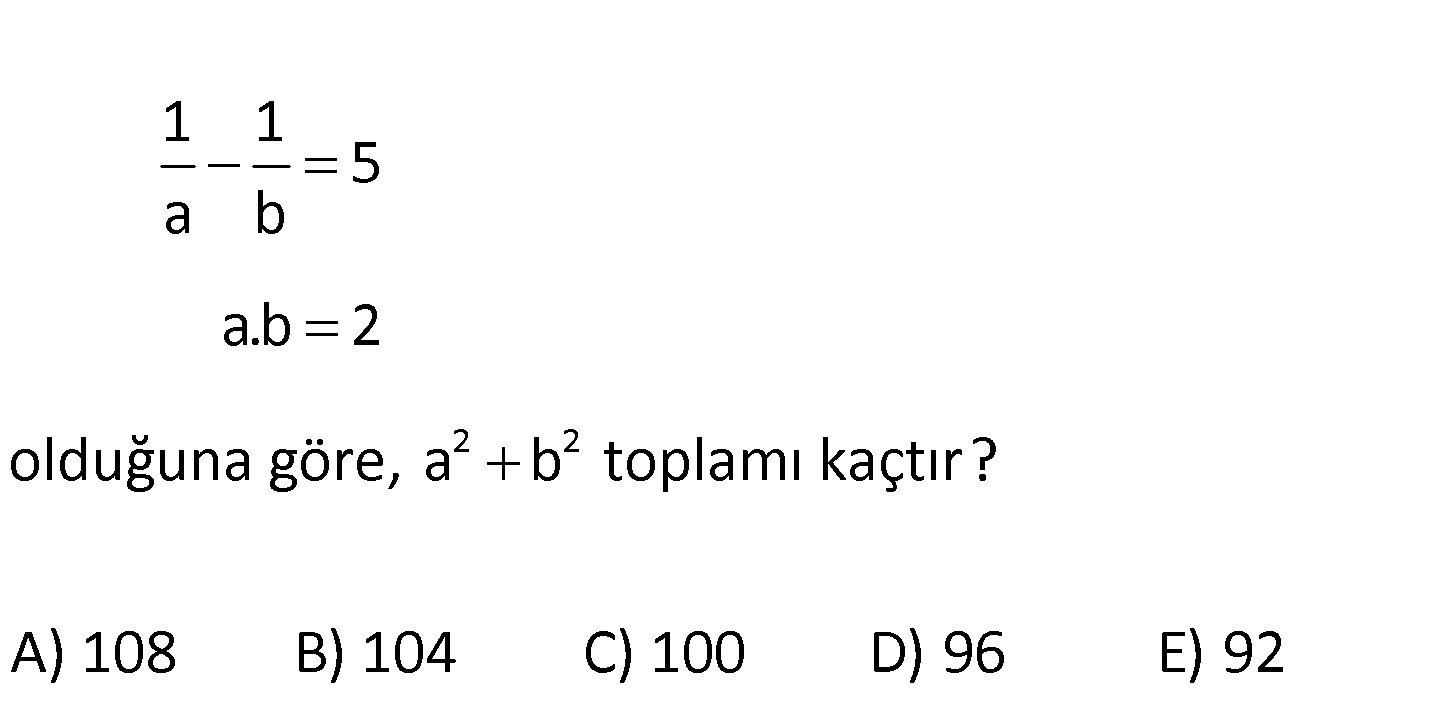

12.SORU
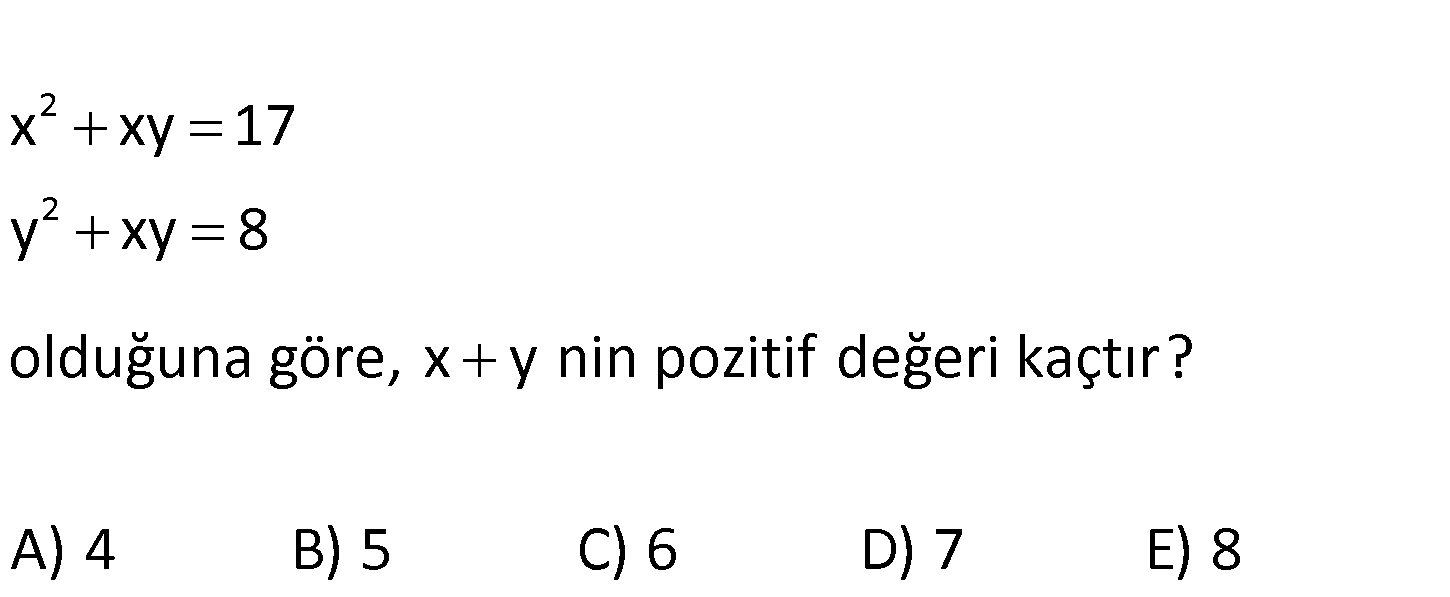

13.SORU


14.SORU


15.SORU
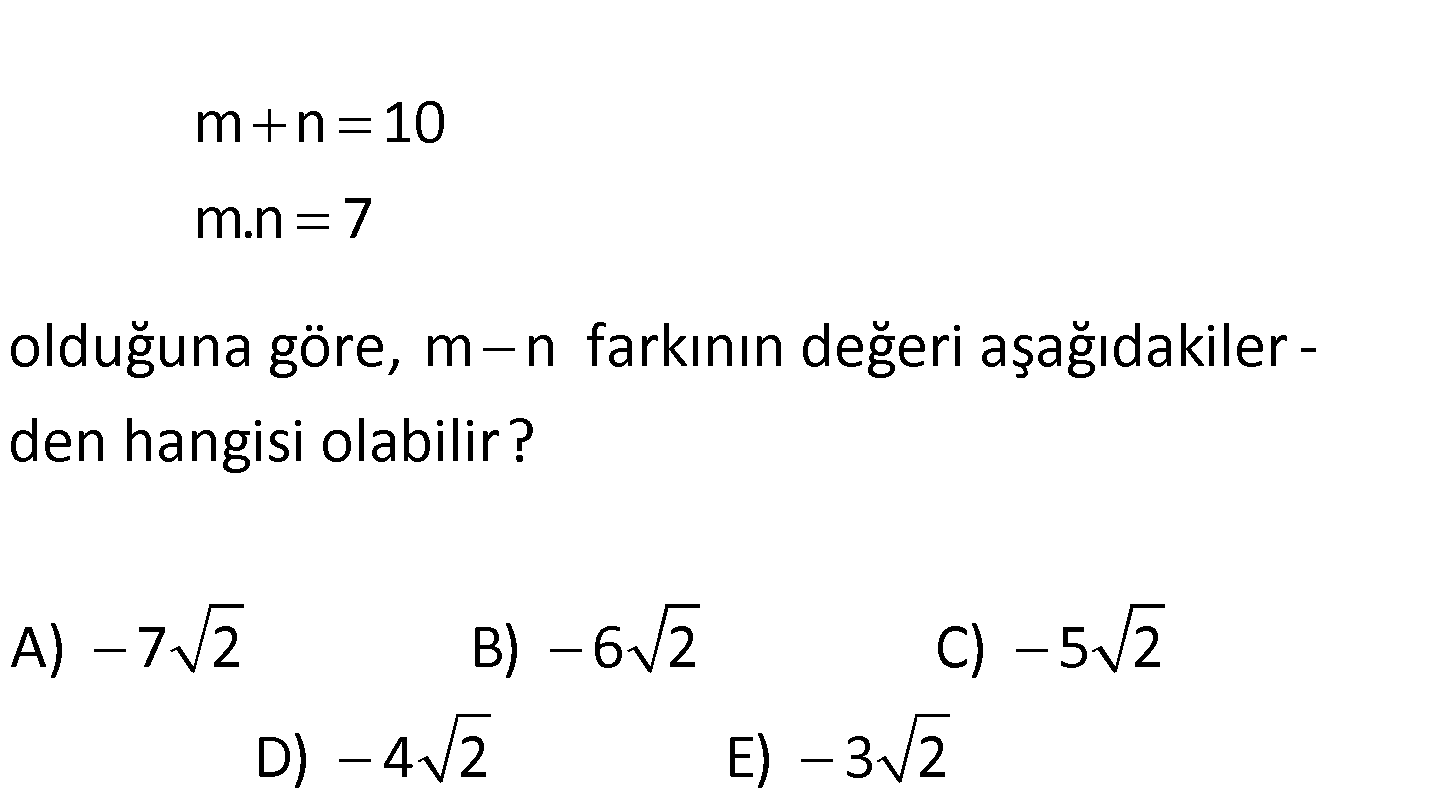
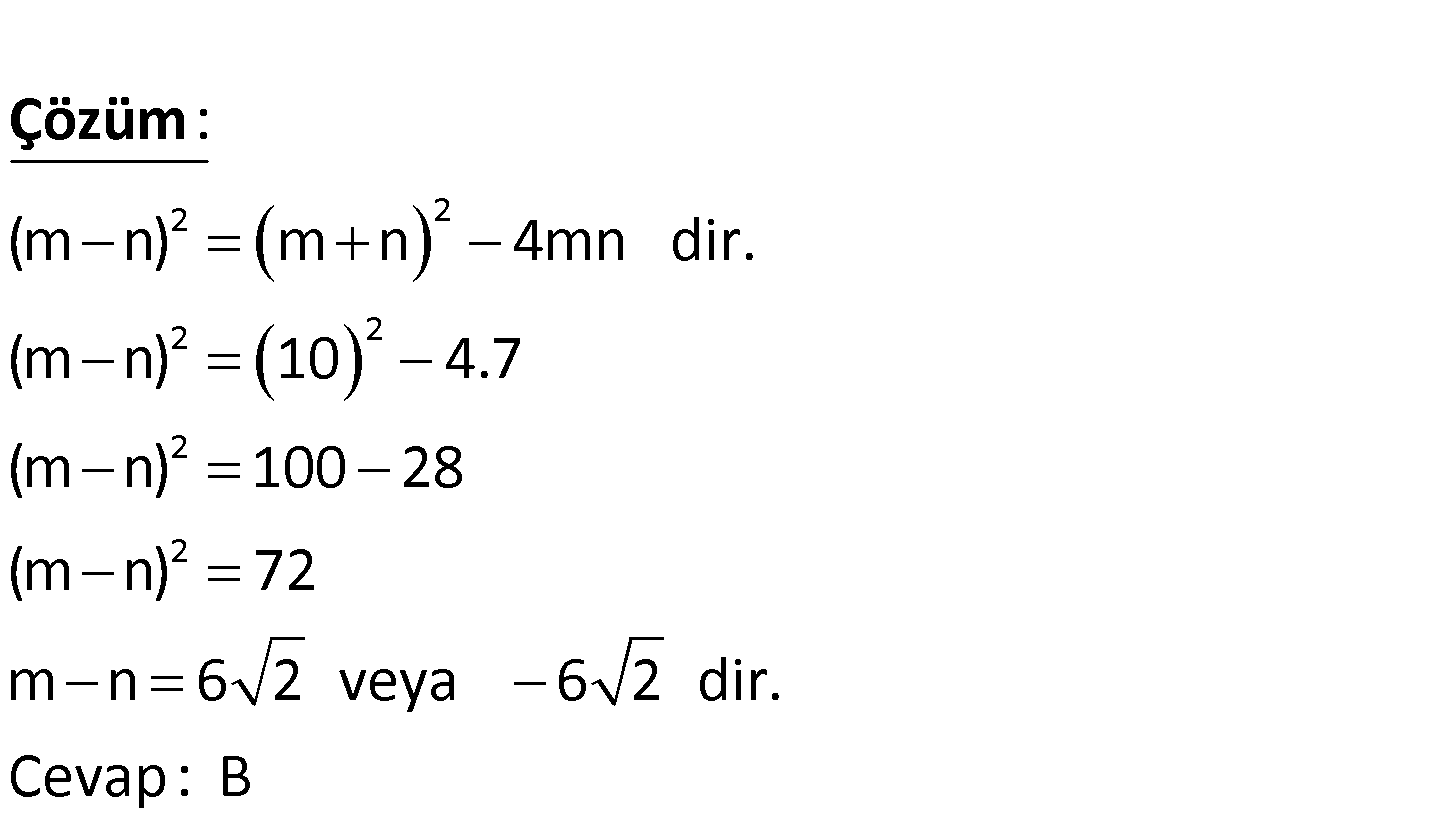
16.SORU
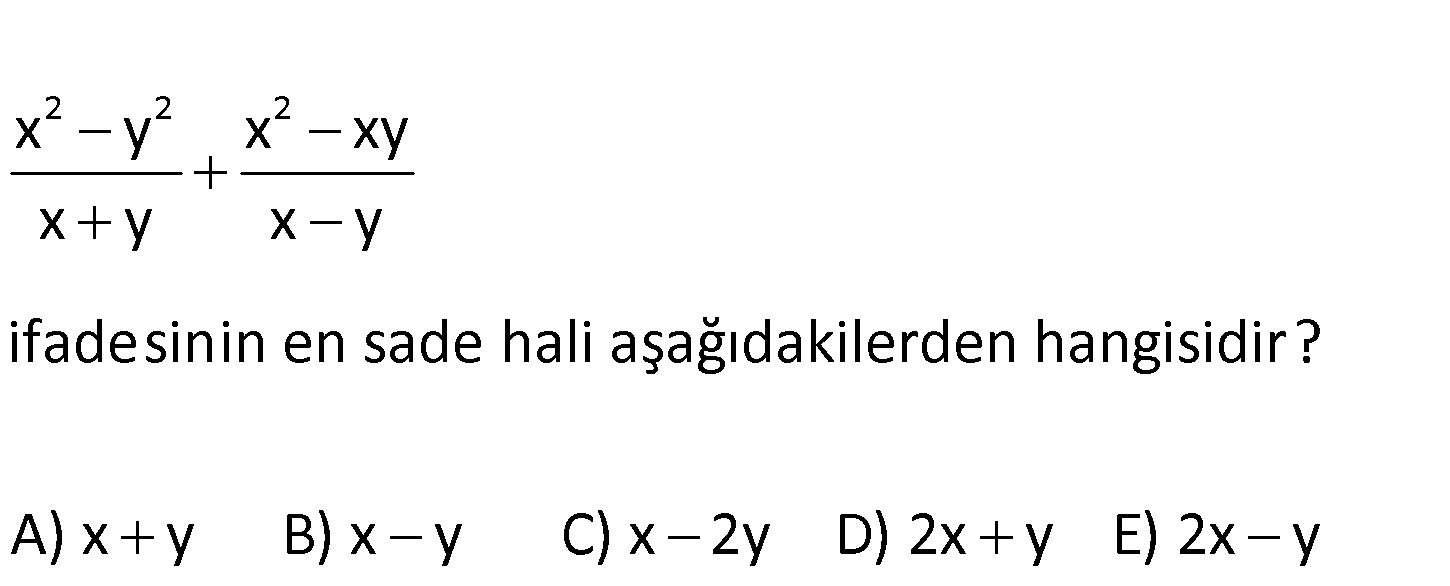
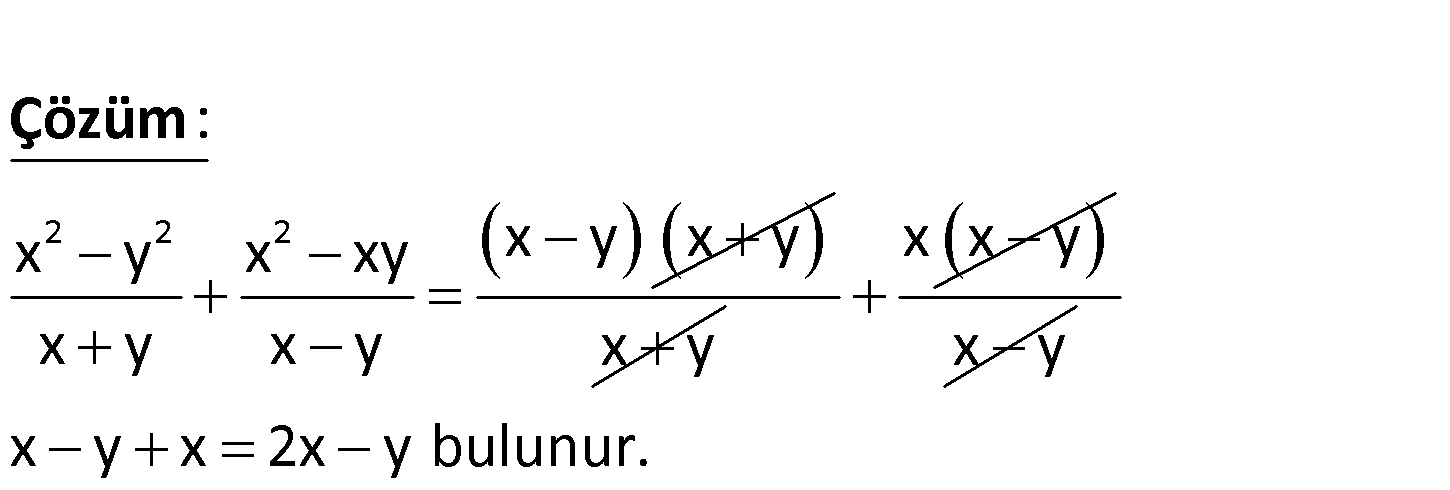
17.SORU

18.SORU


19.SORU

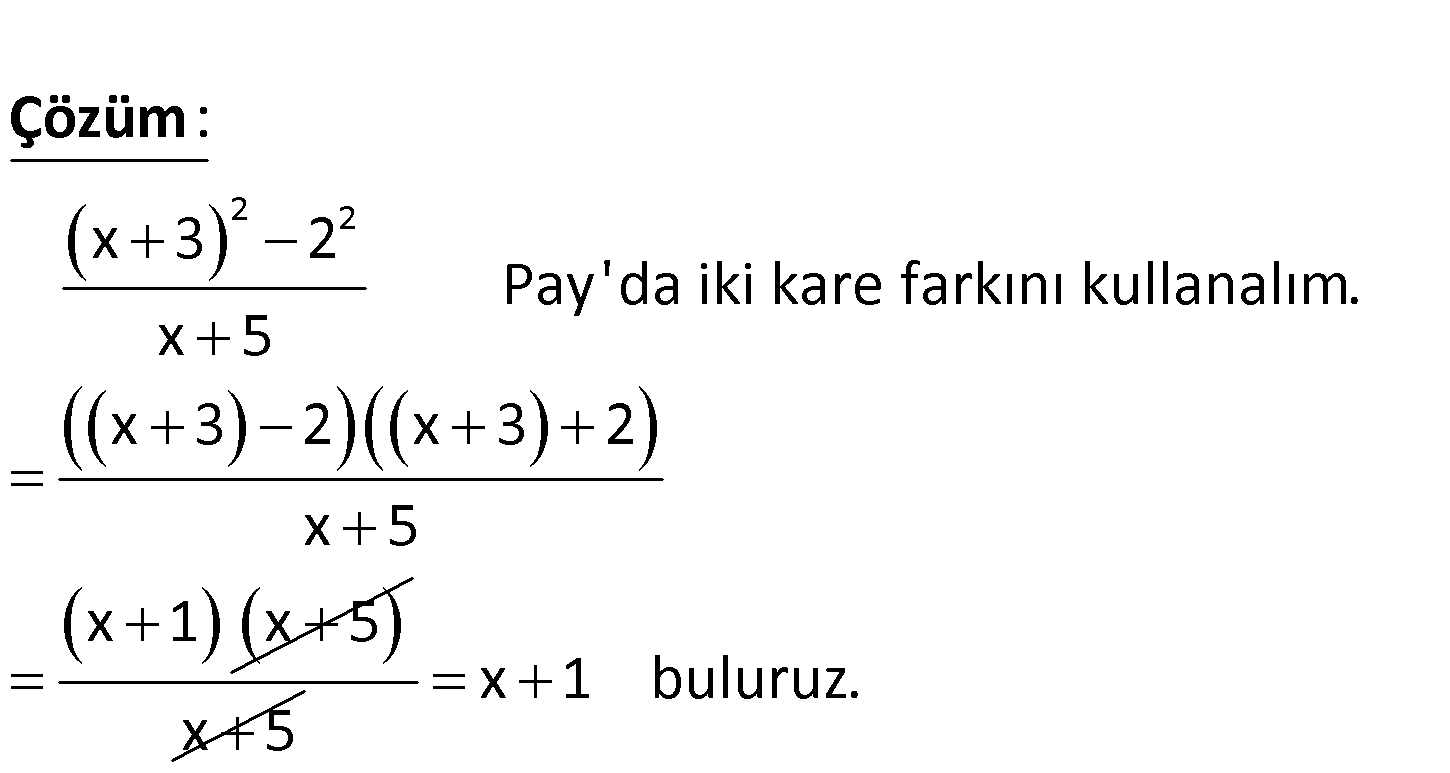
20.SORU
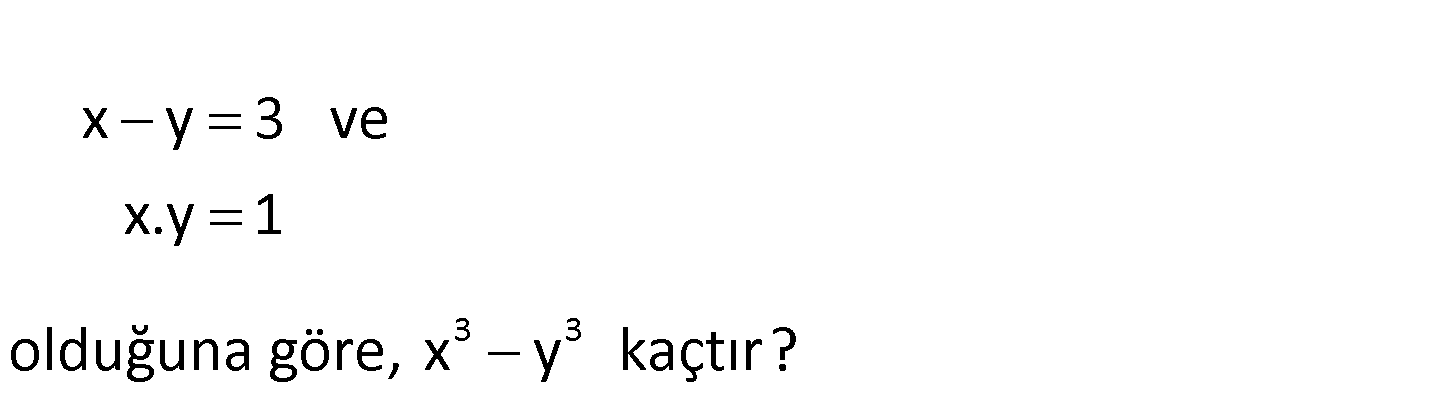
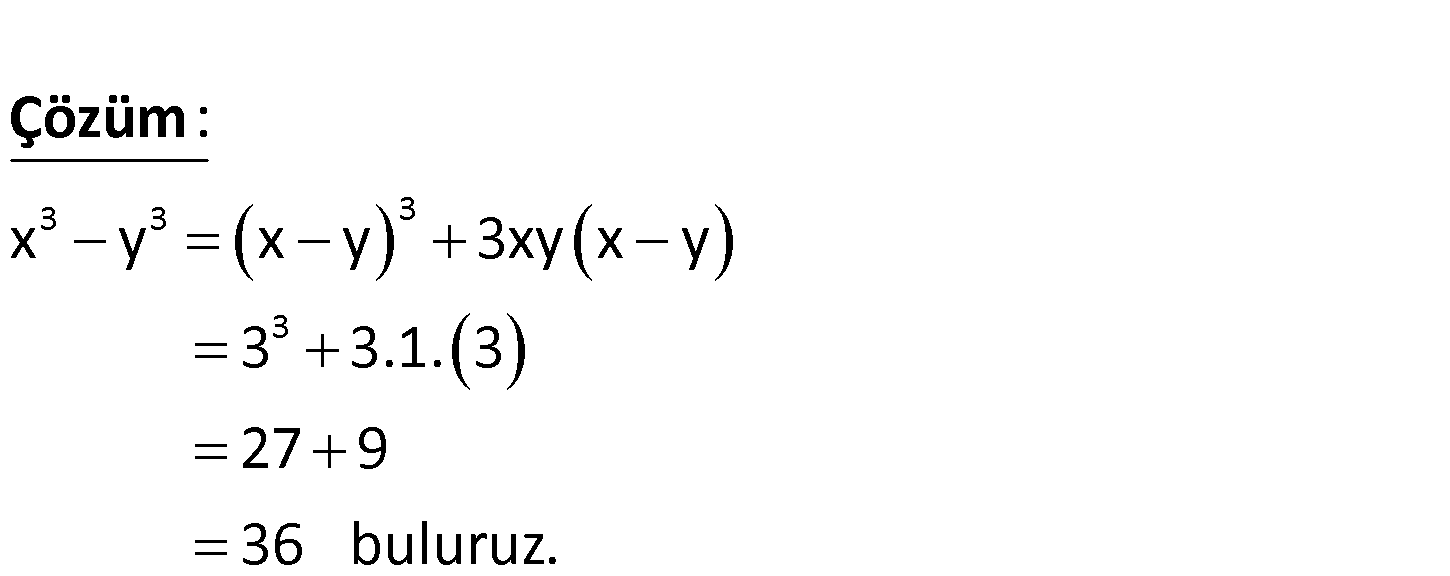
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
Basit çarpanlarına ayırma soruları, Kısa çarpanlarına ayırma soruları
x.y 6 x.z 10 olduğuna göre, x. y z kaçtır? A) 4 B) 1 C) 10 D) 16 E) 18 6 ( 10) x (y z) x y x z 6 ( 10) 6 10 16 buluruz. Do : ğru Cevap : D Şıkkı Çözüm www.matematikkolay.net 14
2 2 a 3b olmak üzere, 4a 2ab ifadesinin değeri kaçtır? 8ab 4a 5 3 5 A) 5 B) C) D) 2 E) 2 2 2 www.matematikkolay.net 2 2 : 4a 2ab 2a 8ab 4a Çözüm (2a b) 4a 2 2a b (2b a) 2(2b a) a 3b yazalım. 2.3b b 6b b 5b 2(2b 3b) 2.( b) 2b 5 bulunur. 2 46
a b 12 ve a.b 30 olduğuna göre, a b nin pozitif değeri kaçtır? A) 2 3 B) 2 5 C) 5 D) 6 E) 2 6 2 2 2 (a b) (a b) 4ab 12 4.30 144 120 24 a b 2 : 4 2 6 buluruz Çözüm . 48
www.matematikkolay.net 2 a 83 b 77 sayıları veriliyor. Buna göre, a b 4ab işleminin sonucu aşağı – dakilerden hangisidir ? A) 1 B) 6 C) 36 D) 160 E) 64240 2 2 2 2 2 2 2 2 (a b) 4ab a 2ab b 4ab a 2ab b (a b) (83 ( 77)) 6 36 buluruz. : Çözüm 66
2 2 2 4 2 4 4 2 4 2 2 2 3x y x işleminin sonucu aşağıdakilerden hangisidir? A) 10x 6xy y B) 9x 6xy y x C) 9x 6x y 2 4 2 2 2 4 2 2 4 y D) 10x 6x y y E) 10x 6xy y www.matematikkolay.net 2 2 2 2 2 4 2 2 2 4 (3x y ) x 9x 6xy y x 10x 6xy y buluru . : z Çözüm 67
2 2 2 5x 6xy 16 4x y 33 olduğuna göre, 3x y nin pozitif değeri aşağıdakilerden hangisidir? A) 4 B) 5 C) 6 D) 7 E) 8 2 2 2 2 2 2 5x 6xy 16 4x y 33 taraf tarafa toplayalım. 9x 6xy y 49 (3x) 2.(3x)(y : ) Çözüm 2 2 y 49 (3x y) 49 3x y 7 buluruz. 68
a.b.c b.c.d c.d.e ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) ab B) bc C) ab bd de D) a E) d www.matematikkolay.net çarpanlardan biri abc bcd cde c.(ab bd de) Cevap: C şıkk : ı Çözüm 77
4ab 4xb 2xy 2ay 2x 2a ifadesinin sadeleştirilmiş şekli aşağıdakilerden hangisidir? A) 2 b y B) 2 y b C) x a D) y 2b E) 2 x y (2x 2a) 4ab 4xb 2xy 2ay 2b(2a 2x) y(2x 2a) 2x 2a 2x 2a (y 2b) (2x 2a : ) Çözüm 2x 2a y 2b buluruz. 78
www.matematikkolay.net 2 2 2 2 1 x y 1 ve x y olduğuna göre, 4 x y 2y 1 x y x y ifadesinin değeri kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5 2 2 2 2 2 2 2 2 iki kare farkı iki kare farkı 2 2 x y 2y 1 x y 2y 1 x y x y x y x y x y 1 x y . x y x : Çözüm x y 1. x y 1 y x y x y 1 1 5 1 4 4 5 4 5 bulunur. 1 1 4 1 4 4 110
www.matematikkolay.net 2 x 2 . x 3 x 6 cebirsel ifadesinin en sade eş değeri aşağıdakiler – den hangisidir? A) 6 B) x C) 2 2 2 x D) x 6 E) x 2 2 her terimi birbiri ile çarpalım 2 2 x 2 . x 3 x 6 x.x x.3 2.x 2.3 x 6 x : Çözüm 3x 2x 6 2 x 6 x bulunur. 118
2 2 1 1 5 a b a.b 2 olduğuna göre, a b toplamı kaçtır? A) 108 B) 104 C) 100 D) 96 E) 92 www.matematikkolay.net (b) (a) 1 1 b a 5 5 a b ab ab b a b a 5 5 b a 10 dur. ab 2 b a 10 iki tarafın d : Çözüm 2 2 2 2 2 2 2 2 a karesini alalım. b a 100 b 2ab a 100 b a 4 100 a b 104 buluruz. 121
2 2 x xy 17 y xy 8 olduğuna göre, x y nin pozitif değeri kaçtır? A) 4 B) 5 C) 6 D) 7 E) 8 2 2 2 2 2 x xy 17 y xy 8 Taraf tarafa toplayalım. x 2xy y 25 x y 25 : Çözüm x y 5 buluruz. 123
2 2 a b 4b ifadesinin çarpanlarından biri aşağıdakilerden hangisidir? A) a 3b B) a b C) a 2b D) a2b E) a2b 2 2 2 2 a b 4b İki kare farkını kullanalım. a b 2b a b 2b a b 2b a b a 3b A şıkkında a 3b ifadesi : Çözüm var. Cevap: A www.matematikkolay.net 131
www.matematikkolay.net 2 2 2 2 a b m a.b n olduğuna göre, a b ifadesi m ve n türünden aşağıdakilerden hangisidir? A) m mn B) 3m 3 3 3 3 mn C) m 3mn D) m 3mn E) m n 3 3 3 3 3 a b a b 3ab(a b) m 3n m m 3 : mn buluruz. Çözüm 134
m n 10 m.n 7 olduğuna göre, m n farkının değeri aşağıdakiler – den hangisi olabilir? A) 7 2 B) 6 2 C) 5 2 D) 4 2 E) 3 2 www.matematikkolay.net 2 2 2 2 2 2 (m n) m n 4mn dir. (m n) 10 4.7 (m n) 100 28 (m n) 72 m n 6 2 veya 6 2 dir. Cevap: : B Çözüm 150
2 2 2 x y x xy x y x y ifadesinin en sade hali aşağıdakilerden hangisidir? A) x y B) x y C) x 2y D) 2x y E) 2 x y 2 2 2 x y x xy x y x y x y x y : Çözüm x y x x y x y x y x 2x y bulunur. 167
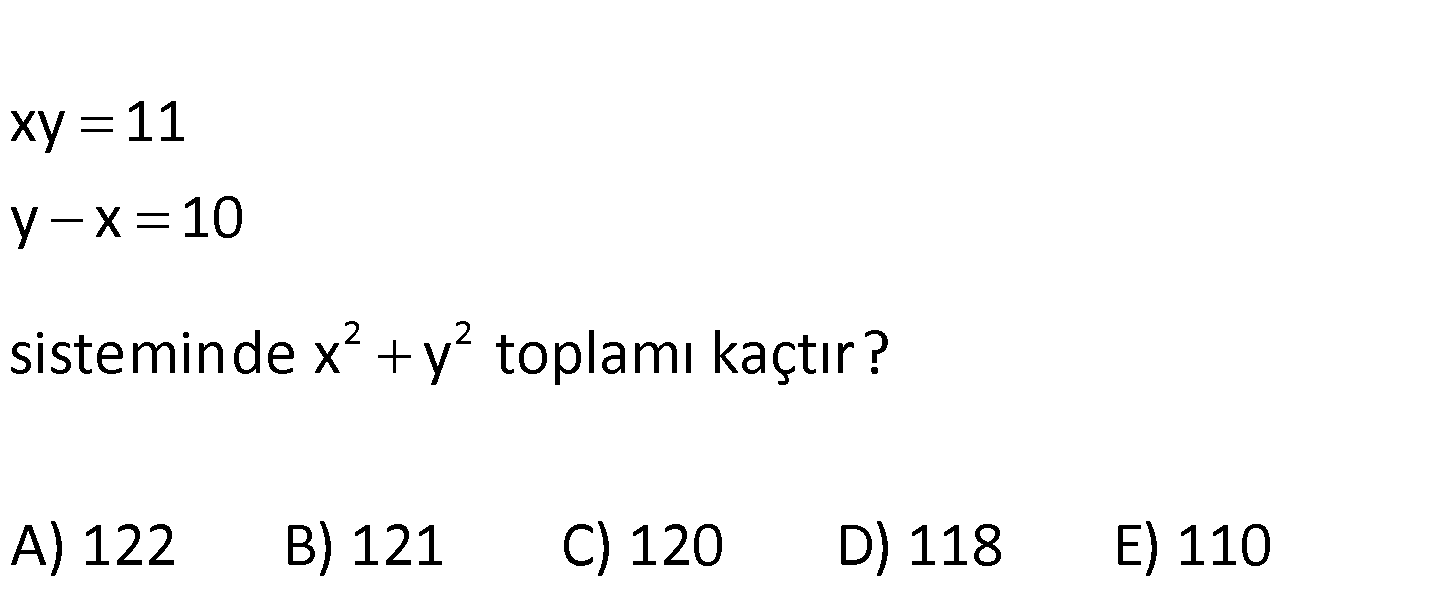
2 2 xy 11 y x 10 sisteminde x y toplamı kaçtır? A) 122 B) 121 C) 120 D) 118 E) 110 2 2 11 2 2 2 2 y x 10 iki tarafın da karesini alalım. y 2xy x 100 y 22 x 100 y x 122 bulu : ruz. Çözüm 172
2 2 x y 7 ve x.y 6 olduğuna göre, x değerini bulunuz y . 2 2 2 2 2 2 6 2 2 2 2 : x y 7 x y 7 x 2xy y 49 x 12 y 49 x y 37 buluruz . Çözüm www.matematikkolay.net 192
www.matematikkolay.net 2 x 3 4 x 5 ifadesinin sadeleştirilmiş biçimi aşağıdakilerden hangisidir? A) x 1 B) x 3 D) x 5 D) 1 E) 2 2 2 x 3 2 Pay’da iki kare farkını kullanalım. x 5 x 3 2 x 3 2 x 5 x 1 x : 5 Çözüm x 5 x 1 buluruz. 206
3 3 x y 3 ve x.y 1 olduğuna göre, x y kaçtır? www.matematikkolay.net 3 3 3 3 x y x y 3xy x y 3 3.1. 3 27 9 36 buluruz : . Çözüm 212

