Soru Sor sayfası kullanılarak Çarpanlara Ayırma konusu altında Ax^2+Bx+C ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
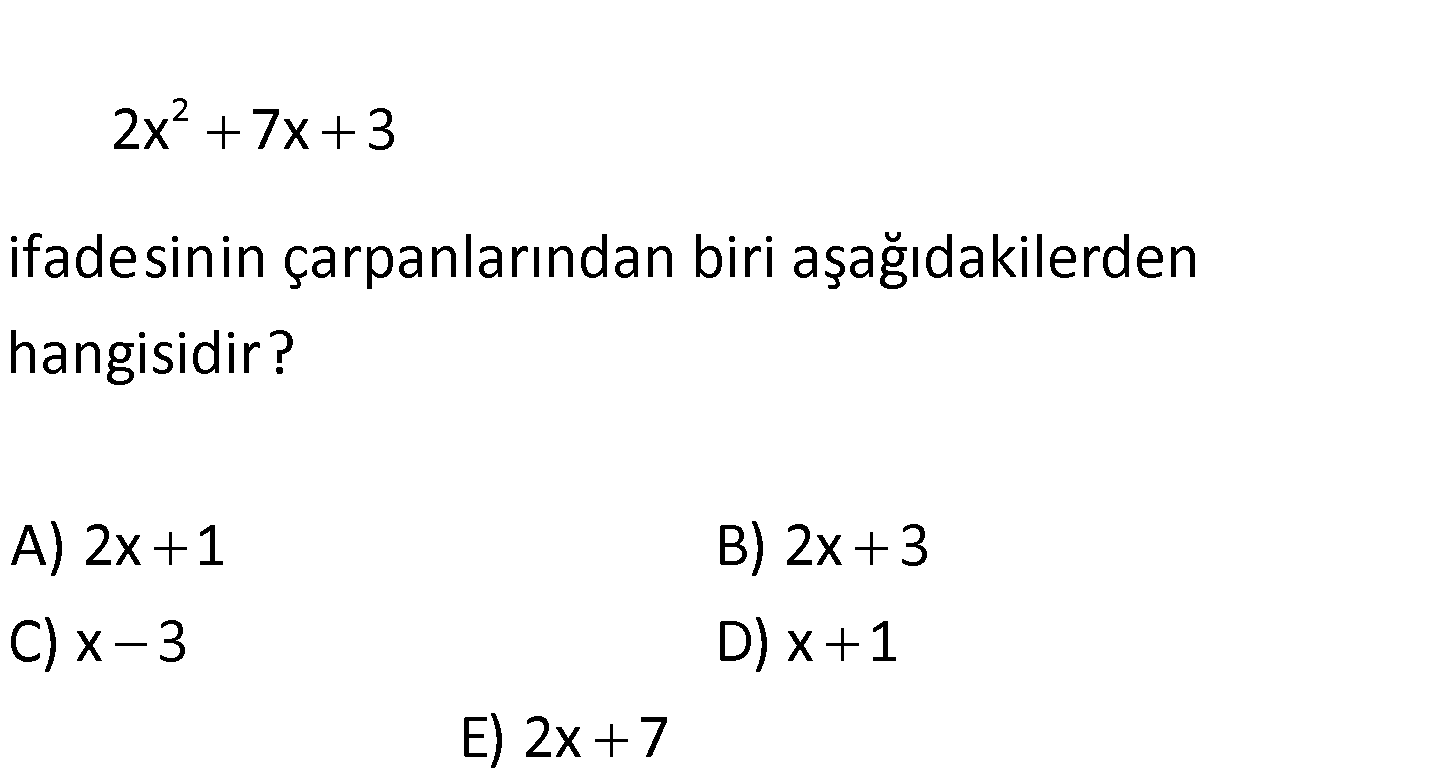
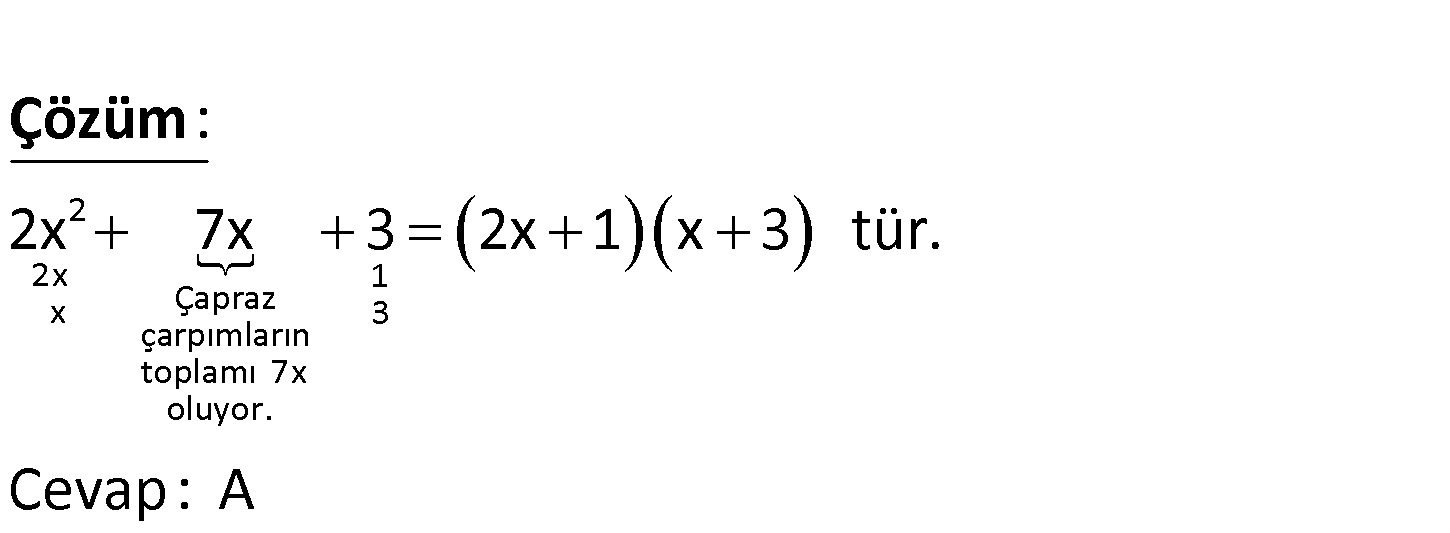
2.SORU


3.SORU
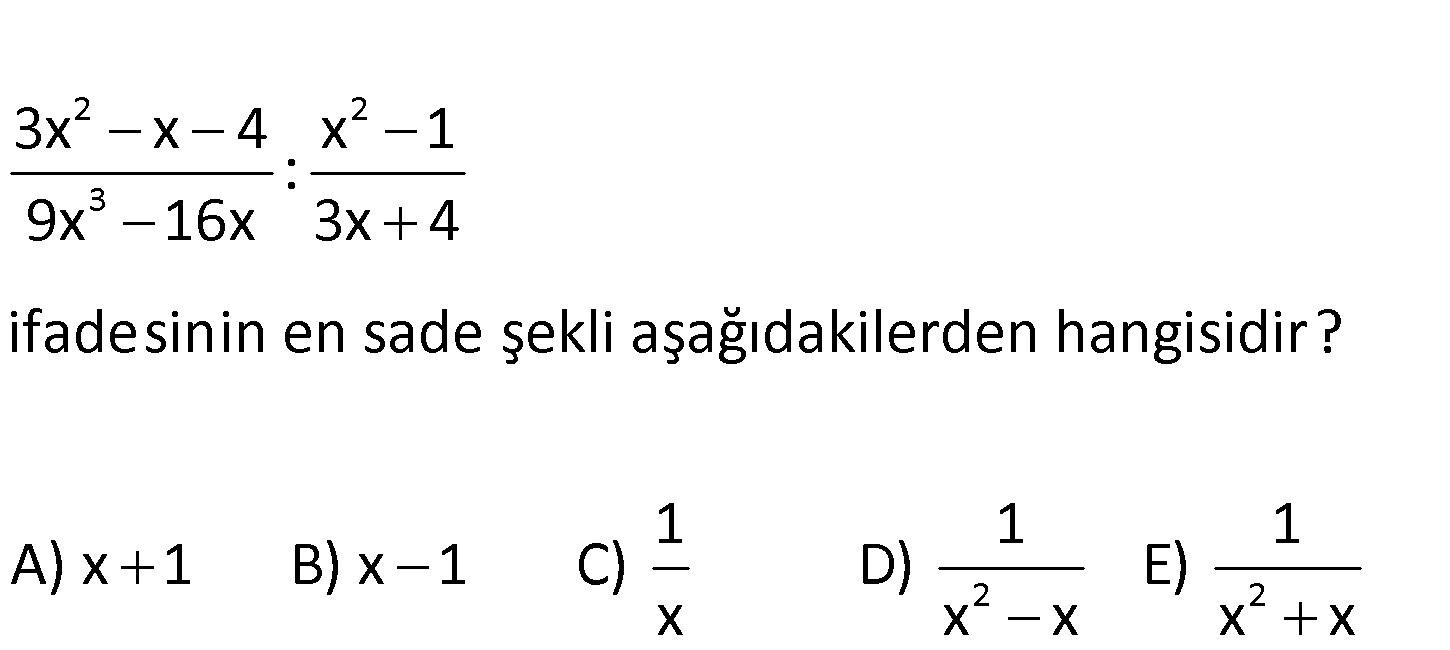
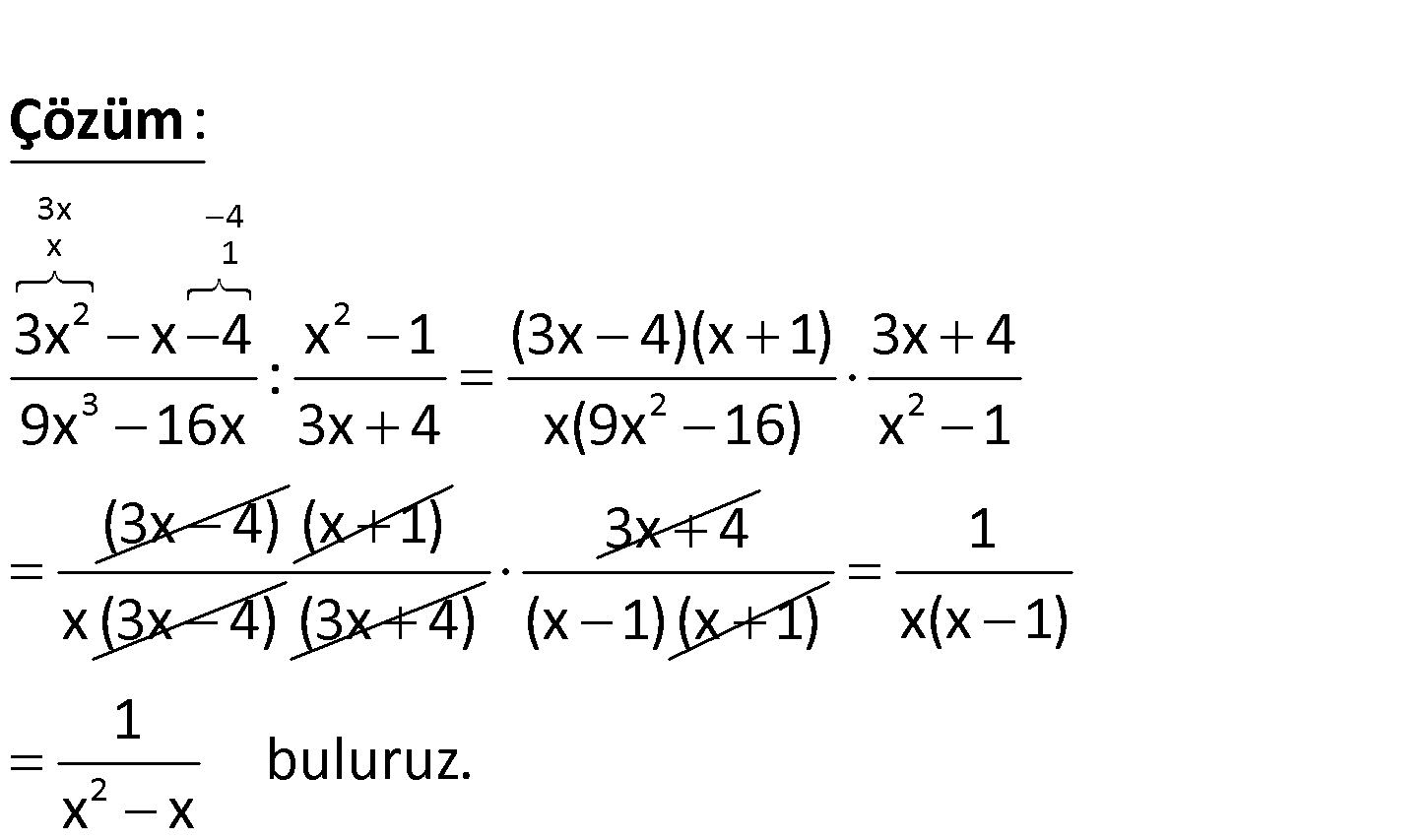
4.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Telif: Çözümler, sitemiz tarafından hazırlanmış olup izinsiz yayınlanıp, çoğaltılması yasaktır.
x^2+Ax+B
2 2 2 2 x Ax B x 4x 21 x 2 ise A B ? x 11x 28 x 9 x 3 2 2 2 2 3 7 3×7 2 2 2 2 7 4 7×4 İki kare f x Ax B x 4x 21 x 2 x 11x 28 x 9 x 3 x Ax B x 4 .x 21 x 11x 28 x 9 : Çözüm arkı 2 2 x 2 x 3 x Ax B (x 3)(x 7) x 2 (x 7)(x 4) (x 3)(x 3) x 3 x Ax B (x 7) (x 3) (x 4) (x 7) (x 3) (x 3) x 2 x 3 2 2 2 6 8 x Ax B (x 2) (x 4) x Ax B x 6x 8 A 6 ve B 8 dir. A B 6 8 14 buluruz. 27
2 x 6x 8 0 x n denkleminin çözüm kümesi bir elemanlı olduğuna göre, n nin alabileceği değerler in farkı aşağıdakiler – den hangisi olabilir? A) 4 B) 3 C) 1 D) 2 E) 3 2 x 6x 8 0 denkleminin çözüm kümesi bir x n elemanlı ise kesrin payı ile paydası sadeleşiyor : Çözüm 2 demektir. x 6x 8 (x 4).(x 2) 0 0 x n x n İfadenin sadeleşebilmesi için; n 4 veya n 2 olmalı. İkisinin farkı; 4 ( 2) 4 2 2 veya 2 ( 4) 2 4 2 olabilir. Şıklarda 2 olduğu için doğru cevap D Şıkkıdır. www.matematikkolay.net 88
2 2 2 2 x 5x 6 x 8x 15 x 9 x 6x 8 ifadesinin en sade hali aşağıdakilerden hangisidir? x 5 x 5 A) B) C) x 3 x 4 x 3 x 2 x 3 D) E) x 2 x 3 x 4 www.matematikkolay.net 3 2 3.2 ( 5) ( 3) ( 5)( 3) 2 2 2 2 İki kare farkı 4 2 4.2 : x 5 x 6 x 8 x 15 x 9 x 6 x 8 (x 3) Çözüm (x 2) (x 3) (x 3) (x 5) (x 3) (x 4) (x 2) x 5 buluruz. x 4 www.matematikkolay.net 127
x 1 x 5 olduğuna göre, x kaçtır? A) 3 B) 5 C) 7 D) 8 E) 10 2 2 8 3 x 1 x 5 iki tarafın da karesini alalım. x 1 x 10x 25 0 x 11x 24 0 : x 8 x 3 x 8 Çözüm veya x 3 tür. Test edelim. x 1 x 5 x 3 olursa 3 1 3 5 2 2 Sağlamadı x 8 olursa 8 1 8 5 3 3 Sağladı Cevap: D 227
2 2 2 x x 2 x 1 : ifadesinin en sade şekli aşağıdaki – x 4 x 2 lerden hangisidir? 1 A) B) x 1 C) 1 D) x 1 E x 1 1 ) x 1 2.1 iki kare farkı 2 2 2 iki karefarkı x x 2 x 1 : x 4 x 2 (x 2) (x 1) (x 1) (x 1) : (x 2) (x 2) x 2 (x 2 : Çözüm ) (x 1) (x 2) (x 2) x 2 (x 1) (x 1) 1 buluruz. x 1 www.matematikkolay.net 29
2 2 x 7x 5 x 7x 1 5 ifadesinin çarpanlarından biri aşağıdakilerden hangisi değildir? A) x B) x 1 C) x 5 D ) x 6 E) x 7 www.matematikkolay.net 2 2 3 2 3 2 2 2 2 (x 7x 5 )(x 7x 1 ) 5 (x 7x 3 2)(x 7x 3 2) 5 iki kare farkı şeklinde : yazabiliriz. (x 7x Çözüm 2 2 2 2 2 2 2 2 2 2 2 1 6 1.6 3) 2 5 (x 7x 3) 9 (x 7x 3) 3 yine iki kare farkını kullanalım. (x 7x 3 3)(x 7x 3 3) (x 7 x 6)(x 7x) (x 1)(x 6)x.(x 7) elde ederiz. C şıkkındaki x 5 bulunmuyor. 156

