Soru Sor sayfası kullanılarak Basit Eşitsizlikler konusu altında Temel eşitsizlik soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
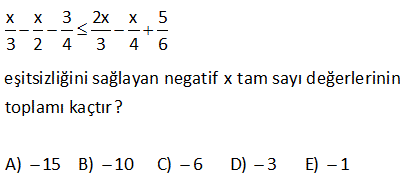

2.SORU


3.SORU


4.SORU
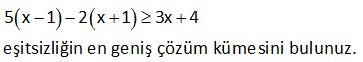
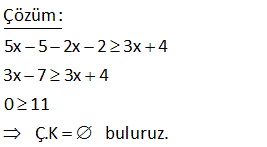
5.SORU


6.SORU


7.SORU
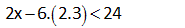

8.SORU
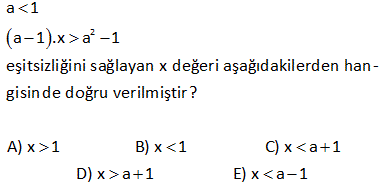

9.SORU
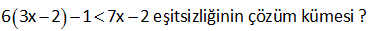
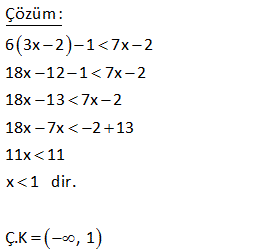
10.SORU


11.SORU
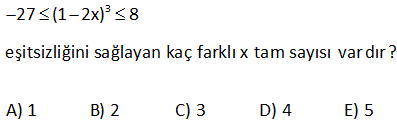

12.SORU


13.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
x x 3 2x x 5 3 2 4 3 4 6 eşitsizliğini sağlayan negatif x tam sayı değerlerinin toplamı kaçtır? A) 15 B) 10 C) 6 D) 3 E) 1 (4) (6) (3) (4) (3) (2) Çözüm: x x 3 2x x 5 Paydaları eşitleyelim 3 2 4 3 4 6 4x 6x 9 8x 3x 10 12 12 12 12 12 12 4x 6x 9 8x 3x 10 2x 9 5x 10 2x 5x 10 9 7x 19 (-) ile çarpılınca eşitsizlik yön değiştirir. 7x 1 9 Bunu sağlayan sadece (-1) ve (-2) negatif tam sayılar vardır. Toplamları 3 buluruz. www.matematikkolay.net 4 7 2x 3 olduğuna göre, 3x in alabileceği en büyük tam sayı değeri kaçtır? A) 11 B) 12 C) 9 D) 10 E) 8 Çözüm: 7 2x 3 Her tarafı 3 / 2 ile çarpalım. 21 9 3x 2 2 10,5 3x 4,5 En büyük 10 olabilir. www.matematikkolay.net 9 x bir gerçek sayı olmak üzere, 5x 3 x 4 3 eşitsizliğini sağlayan farklı x doğal sayılarının topla – mı kaçtır? A) 3 B) 6 C) 10 D) 15 E) 21 Çözüm: 5x 3 x 4 3 5x 3 3x 12 2x 9 x 4,5 0,1,2,3,4 değerleri olabilir. Toplamları 10 dur. www.matematikkolay.net 12 5x 1 2x 1 3x 4 eşitsizliğin en geniş çözüm kümesini bulunuz. www.matematikkolay.net Çözüm: 3x 4 3x 7 3x 4 0 11 Ç.K bul 5x 5 2x 2 uruz. 21 5 katı 30 fazlasından küçük olmayan bir tam sayının 3 katı , 21 fazlasından büyük değildir. Bu koşula uyan tam sayıların toplami kaçtır? A 18 B 21 C 24 D ) ) ) )27 E)32 Çözüm: 5x x 30 ise 4x 30 x 7,5 tir. Ayrıca; 3x x 21 ise 2x 21 x 10,5 tir. Buna göre; x’in alabileceği tam sayı değerleri: 8, 9 ve 10’dur. Toplamları ise 27 dir. Cevap: 27 www.matematikkolay.net 25 x 1 olmak üzere, 2xy 6 6x 2y eşitsizliğini sağlayan y nin alabileceği en küçük tam sayı değeri kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 www.matematikkolay.net Çözüm: 2xy 6 6x 2y 2xy 2y 6x 6 2y(x 1) 6(x 1) iki tarafı da (x 1) ile sadeleşti – relim. x , 1 den küçük olduğu için (x 1) negatiftir. Eşitsizlik yön değiştirecektir. 2y 6 y 3 tür. y en az 4 olabilir. 40 2x 6.2.3 24 2x 6.2.3 24 2x 6.6 24 2x 36 24 2x 60 x Çö 30 buluruz. züm: 45 2 a 1 a 1 .x a 1 eşitsizliğini sağlayan x değeri aşağıdakilerden hangisinde doğru verilmiştir ? A) x 1 B) x 1 C) x a 1 D) x a 1 E) x a 1 www.matematikkolay.net 2 negatif Çözüm: a 1 a 1 0 dır. a 1 .x a 1 her tarafı a 1 e bölelim. Negatif sayıya böldüğümüz için eşitsizlik yön değiştirir. a 1 a1 2 a 1 .x a 1 (a 1) x (a 1) a 1 x a1 buluruz. 48 63x 217x 2 eşitsizliğinin çözüm kümesi ? Çözüm: 6 3x 2 1 7x 2 18x 12 1 7x 2 18x 13 7x 2 18x 7x 2 13 11x 11 x 1 dir. Ç.K , 1 49 x 3 3x 10 x 18 eşitsizliğini sağlayan kaç farklı x tam sayısı var dır? Çözüm: x 3 3x 10 x 18 her taraf tan x çıkaralım. 3 2x 10 18 olur. Her tarafa 10 ekleyelim. 13 2x 28 olur. Her tarafı 2′ ye bölelim. 6,5 x 14 olur. x 7,8,9,10,11,12,13 o labilir. 7 farklı tam sayı değeri vardır. 56 3 27 (1 2x) 8 eşitsizliğini sağlayan kaç farklı x tam sayısı var dır? A) 1 B) 2 C) 3 D) 4 E) 5 www.matematikkolay.net 3 3 3 3 Çözüm: 27 (1 2x) 8 ( 3) (1 2x) 2 3 1 2x 2 3 1 2x 2 1 4 2x 1 4 2x 1 1 2 x 2 2 2 2 Şimdi eşitsiziğin her tarafını ( ) ile çarparsak eşitsizlik yön değiştirir. 1 x 2 dir. 2 Buna göre x {0,1,2} 3 t ane buluruz. 11 a ve b pozitif tam sayılardır. x a 0 x b eşitsizliğini sağlayan 11 tane x tam sayısı olduğuna göre, a b toplamı kaçtır? A) 12 B) 11 C) 10 D) 9 E) 8 www.matematikkolay.net 11 tam sayı Çözüm: x a 0 b x a x b x’in alabileceği en büyük tam sayı değeri a 1 En küçük tam sayı değer b 1 dir. Terim sayısı a 1 ( b 1) 1 11 ise; a 1 b 1 1 1 1 a b 1 11 a b 12 buluruz. 19 x asal sayı ve çift sayıdır. 5 x 10 8 y 5 olduğuna göre, 2x y ifadesinin en büyük değeri kaçtır? A) 10 B) 12 C) 16 D) 20 E) 28 Çözüm: x sayısı asal ve çit ise kesinlikle 2 olmak zorundadır. Başka çift asal sayı yoktur. 2x y ifadesinin büyük olması için y en küçük değerini almalı. y 7 olur. 2.x y 2.2 7 4 7 11 bulunur. 36


13.soruda cevap 11 ama şıklarda 11 şıkkı yok
Uyarınız için teşekkürler. Hata düzeltildi.
7. sorunun tamamı yok sadece eşitsizlik yazıyor soruyu anlamadım.
x in aralığı isteniyor.