Soru Sor sayfası kullanılarak Basit Eşitsizlikler konusu altında Tam kare ifade bulunan eşitsizlikler ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU


5.SORU


6.SORU
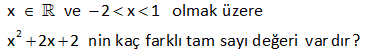

7.SORU


8.SORU


9.SORU


Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
4 x 0 |x 3| eşitsizliğini sağlayan 10 dan küçük kaç tane x doğal sayısı var dır? A) 8 B) 7 C) 6 D) 5 E) 4 4 4 Çözüm: x 0 |x 3| x ifadesinin derecesi çift olduğundan, her zaman pozitiftir. |x 3| ifadesi de mutlak değer olduğundan her zaman pozitiftir. Pozitif bir sayı, pozitif bir sayıya bölündüğünde yine pozitif bi r sayı çıkar. (Yani 0’dan büyük olur.) Ancak, x 3 sayısı paydayı 0 yapacağından, kesir tanımsız olur. Bir de x 0 sayısı Kesiri 0 yapar. Bunu da alamayız. Bunların dışındaki tüm doğal sayılar eşitsizliği sa ğlar 1,2,4,5,6,7,8,9 8 tane www.matematikkolay.net 22 2 1 x 5 olduğuna göre, x 4x ifadesinin tüm değerleri hangi aralıktadır? A) [-4,5] B) [-3,9) C) [-2,9) D) [-1,8) E) [-4,5) www.matematikkolay.net 2 2 2 2 2 2 Çözüm: x 4x ifadesine 4 ekleyip 4 çıkaralım. x 4x 4 4 (x 2) 4 olur. x 2 için, bu ifade en küçük değerini alır. (2 2) 4 0 4 4 tür. 1 x 5 ise; x 5 için (x 2) 4 3 4 9 4 5 tir. 2 O halde x 4x ifadesi [4, 5) aralığındadır. 28 2 x bir reel sayı olmak üzere, x 1 0 2x 4 olduğuna göre, x in alabileceği değerlerin en geniş aralığı aşağıdakilerden hangisidir? A) x 2 B) x 2 C) x 2 D) x 2 E) 1 x 2 2 2 2 Çözüm: x ifadesi negatif olamaz. Bu sebeple x 1 ifadesi daima pozitiftir. x 1 0 2x 4 ifadesi de pozitif olmalıdır. 2x 4 Payda 0 olamaz. Aksi halde kesir tanımsız olur. 2x 4 0 2x 4 x 2 dir. Cevap: B 39 www.matematikkolay.net 2 2 3 a 2 2 b 3 olduğuna göre, a b ab ifadesinin kaç farklı tam sayı değeri var dır? A) 30 B) 29 C) 28 D) 27 E) 26 2 2 2 2 Çözüm: En küçük değer a 0 ve b 0 olduğunda a b ab 0 dır. a 2 ve b 3 seçilerek en büyük değerin üst sınırı görülür. (Veya a -3, b -2) a b ab 9 4 6 19 ‘dan küçük olacak En büyük tam sayı değeri 18 dir. 0 ‘dan 18’e kadar değerler alabilir. Toplam 19 farklı tam sayı değeri alabilir. 46 2 a ve b gerçel sayıları için 0 a 4 4 b 16 eşitsizlikleri veriliyor. Buna göre, a b toplamının alabileceği kaç farklı tam sayı değeri vardır? A) 4 B) 6 C) 8 D) 10 E) 12 www.matematikkolay.net 2 Çözüm: 4 b 16 b pozitif bir sayı olsa 2 b 4 tür. b negatif bir sayı olsa 4 b 2 dir. 0 a 4 idi. 2 b 4 taraf tarafa toplarsak; 2 a b 8 olur. a b 3,4,5,6,7 5 farklı tam sayı 0 a 4 idi. 4 b 2 taraf tarafa toplarsak; 4 a b 2 olur. a b 3, 2, 1,0,1 5 farklı tam sayı Toplam 10 farklı tam sayı değeri var dır. 54 2 x ve 2 x 1 olmak üzere x 2x 2 nin kaç farklı tam sayı değeri vardır? 2 2 2 En az 0 2 2 Çözüm: x 2x 2 x 2x 1 1 x 1 1 En az 1 olur. x 1 olsaydı; x 1 1 2 1 5 olurdu. Ancak x 1 olduğu için bu ifade en fazla 4 olabilir. O zaman bu ifade; 1,2,3,4 4 farklı tam sayı değeri alabilir. www.matematikkolay.net 55 2 2 6 x 2 4 y 3 olduğuna göre, x y ifadesinin alabileceği tam sayı değeri, en küçük tam sayı değerinden kaç fazladır? A) 47 B) 48 C) 49 D) 50 E) 51 2 2 2 2 2 2 Çözüm: x en fazla ( 6) 36’ya yakın bir sayı, en az da 0 olabilir. y en fazla ( 4) 16’ya yakın bir sayı, en az da 0 olabilir. x y en fazla 36 16 52’ye en yakın tam sayı olarak 51 ol 2 2 abilir. x y en az 0 olabilir. Aradaki fark 51 0 51 buluruz. 13 2 2 x ve y gerçel sayılar 5 x 4 2 y 1 olduğuna göre, x y ifadesinin alabileceği tam sayı değerleri kaç tanedir? A) 28 B) 29 C) 30 D) 31 E) 32 www.matematikkolay.net 2 2 2 2 2 2 Çözüm: x y ifadesini en küçük yapmak için sayıları 0 seçelim. x y 0 0 0 (en küçük değer) x y ifadesini büyük yapmak için de sayıları mutlak değerce en büyük sayıları seçelim. x 5 , y 2 s 2 2 2 2 2 2 eçersek, en büyük ifadeyi yakalarız. x y ( 5) ( 2) 25 4 29 dur. (en büyük ) x y ifadesi 0’dan 29’a kadar tüm değerleri alabiliyor 0,1,2,…,29 30 farklı değer. 14 2 x ve y gerçel sayılar 4 x 3 1 y 5 olduğuna göre, x y ifadesinin alabileceği tam sayı değerleri kaç tanedir? A) 23 B) 22 C) 21 D) 20 E) 10 www.matematikkolay.net 2 2 2 2 2 Çözüm: x y ifadesini en küçük yapmak için sayıları x 0 , y 1 seçelim. seçelim. x y 0 1 1 (en küçük değer) x y ifadesini en büyük yapmak için de sayıları x 4 , y 4 seçelim. x y ( 4) 4 2 16 4 20 dir. (en büyük ) x y ifadesi 1’den 20’ye kadar tüm değerleri alabiliyor 1,0,1,2,…,20 22 farklı değer. 15

