Soru Sor sayfası kullanılarak Basit Eşitsizlikler konusu altında Hepsini eşit kabul ederek soru çözme ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU


4.SORU
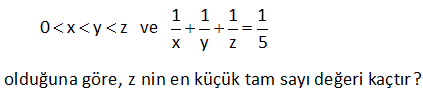

5.SORU


6.SORU
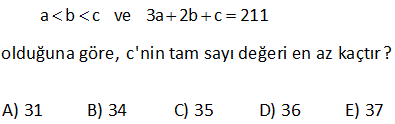

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
2 a b c 4 olduğuna göre, a 2b 4c ifadesinin alabileceği kaç farklı tam sayı değeri var dır? A) 11 B) 12 C) 13 D) 14 E) 15 Çözüm: 2 a b c 4 a b c 2 seçip, a 2b 4c’nin hangi değerden büyük olması gerektiğini bulabiliriz. a 2b 4c 2 2.2 4.2 2 4 8 14 tür. a b c 4 seçip, a 2b 4c’nin hangi değerden küçük olması gerektiğini bulabil iriz. a 2b 4c 4 2.4 4.4 4 8 16 28 dir. 14 a 2b 4c 28 15 ‘ten 27’ye kadar kaç tam sayı var, bulalım. 27 15 1 12 1 13 buluruz. 1 32 a b c 0 1 1 1 1 a b c 6 olduğuna göre, a’nın en küçük tam sayı değeri kaçtır? A) 12 B) 16 C) 18 D) 19 E) 24 Çözüm: Hepsi birbirine eşit olsaydı, 1 1 1 1 k k k 6 3 1 k 6 k 18 olurdu. Ancak a sayısı hepsinden büyük olduğundan, 18 sayısından da büyük olmak zorundadır. Bu sebeple en küçük a tam sayısı 19 dur. www.matematikkolay.net 38 x, y, z pozitif gerçel sayılardır. 1 1 1 1 x y z ve x y z 12 olduğuna göre, z nin en küçük tam sayı değeri kaçtır? A) 24 B) 32 C) 36 D) 37 E) 48 www.matematikkolay.net Çözüm: x y z olsaydı, 1 1 1 1 1 1 1 1 3 1 x y z 12 z z z 12 z 12 z 36 olurdu. Ancak z, diğerlerinden daha büyük olduğu için en küçük tam sayı değeri 37 olur. 41 1 1 1 1 0 x y z ve x y z 5 olduğuna göre, z nin en küçük tam sayı değeri kaçtır? Çözüm: x y z olsaydı, 1 1 1 1 1 1 1 1 3 1 x y z 5 z z z 5 z 5 z 15 olurdu. Ancak z, diğerlerinden daha büyük olduğu için en küçük tam sayı değeri 16 olur. 42 www.matematikkolay.net x, y, z pozitif gerçek sayılar x y z 2 4 6 1 x y z 3 olduğuna göre, x aşağıdakilerden hangisi olabilir? A) 35 B) 36 C) 37 D) 38 E) 39 Çözüm: x y z olsaydı; 2 4 6 1 x y z 3 2 4 6 1 x x x 3 12 1 x 36 dır. x 3 x sayısı hepsinden küçük olduğu için 36’dan küçük olmalıdır. Cevap: A 50 a b c ve 3a 2b c 211 olduğuna göre, c’nin tam sayı değeri en az kaçtır? A) 31 B) 34 C) 35 D) 36 E) 37 Çözüm: a b c olsaydı 3a 2b c 211 3c 2c c 211 6c 211 c 35,166… olurdu. Ancak a b c olduğu için c sayısı bu değerden büyük olmalıdır. Buna göre; c 36 olabilir (en az) (a ve b tam sayı denmediği için d irekt bu şekilde hesaplayabiliriz) Cevap: 36 23

