Soru Sor sayfası kullanılarak Basit Eşitsizlikler konusu altında Eşitsizlikte taraf tarafa toplama ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU
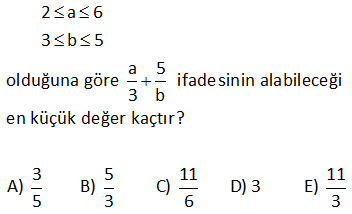

2.SORU


3.SORU


4.SORU


5.SORU
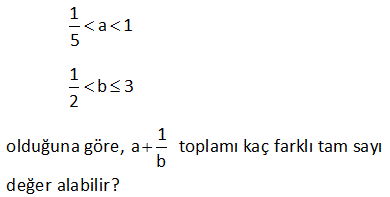
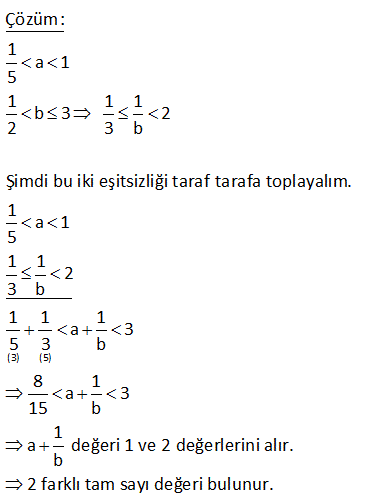
Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
2 a 6 3 b 5 a 5 olduğuna göre ifadesinin alabileceği 3 b en küçük değer kaçtır? 3 5 11 11 A) B) C) D) 3 E) 5 3 6 3 www.matematikkolay.net Çözüm: 2 a 6 ise her tarafı 3’e bölelim 2 a a 2 2 en az olabilir. 3 3 3 3 3 b 5 ise eşitsizliği ters çevirelim 1 1 1 her tarafı 5 ile çarpalım 5 b 3 5 5 5 1 en az 1 olabilir. b 3 b a 5 3 2 5 en az 1 olabilir. b 3 3 Cevap: B şıkkı 7 x ve y gerçel sayıları için 3 x y 7 4 x 2 olduğuna göre, y nin alabileceği tam sayı değerleri toplamı kaçtır ? A) 55 B) 35 C) 20 D) 54 E) 84 Çözüm: 3 x y 7 eşitsizliğin her tarafını – 1 ile çarparsak eşitlik yön değişitirir. 7 y x 3 olur. 4 x 2 eşitsizliği ile toplayalım. 7 y x 3 11 y 1 dir. Bunu sağlayan y tam s ayı değer – leri 2, 3, 4, 5, 6, 7, 8, 9, 10 Toplamı 54 tür. 10 a ve b reel sayılar olmak üzere, 4 x 1 5 y 2 9 10 olduğuna göre, ifadesinin en büyük 2x 1 y tam sayı değeri kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 www.matematikkolay.net Çözüm: 4 x 1 her tarafı 2 ile çarpalım. 8 2x 2 her tarafa 1 ekleyelim. 9 2x 1 3 çarpmaya göre ter sini alalım 1 1 1 9 ile çarpalım 9 2x 1 3 9 1 3 tür. Diğer eşitsizliğe bakalım şimdi. 2x 1 5 y 2 çarpmaya göre ter sini alalım 1 1 1 her tarafı 10 ile çarpalım 5 y 2 10 2 5 dir. Bulduğumuz bu iki eşitsizliği y taraf tarafa toplarsak; 9 10 1 2 3 5 2x 1 y 9 10 3 8 elde ederiz 2x 1 y . Buna göre; sorulan ifade 8 den küçük olmalıdır. Yani en fazla 7 olabilir. 20 x, y ve z birer reel sayı olmak üzere, x y 4 z 3x 11 y z 3 olduğuna göre, x y z toplamının alabileceği en büyük tam sayı değeri kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 www.matematikkolay.net Çözüm: x 3y 4 eşitsizliğin her iki tarafını 1 ile çar – palım. x 3y 4 olur. y z 3 eşitsizliğin her iki tarafını 1 ile çar – palım. y z 3 olur. x 3y 4 z 3x 11 y z 3 taraf tarafa toplayalım. 2x 2y 2z 12 olur. 2.(x y z) 12 x y z 6 dır. Buna göre; x y z’nin en büyük tam sayı değeri 5′ tir. 24 1 a 1 5 1 b 3 2 1 olduğuna göre, a toplamı kaç farklı tam sayı b değer alabilir? (3) (5) Çözüm: 1 a 1 5 1 1 1 b 3 2 2 3 b Şimdi bu iki eşitsizliği taraf tarafa toplayalım. 1 a 1 5 1 1 2 3 b 1 1 1 a 3 5 3 b 8 1 a 3 15 b 1 a değeri 1 ve 2 değerlerini alır. b 2 farklı tam sayı değeri bulunur. www.matematikkolay.net 31

