Soru Sor sayfası kullanılarak Asal Sayılar ve Aralarında Asal Sayılar konusu altında Nitelikli Aralarında Asallık Soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU


3.SORU
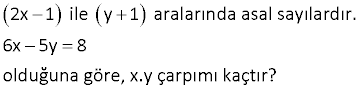

4.SORU


5.SORU

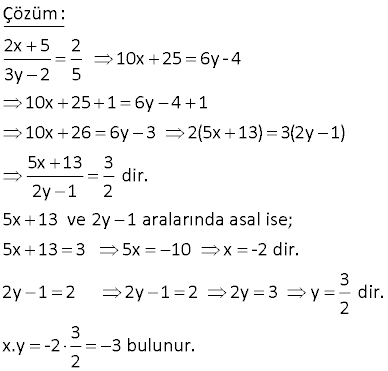
6.SORU


7.SORU


8.SORU


9.SORU


10.SORU


11.SORU


12.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
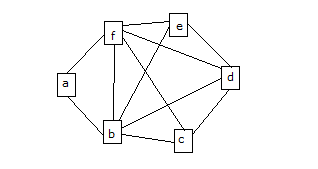
İki pozitif tam sayının en büyük ortak böleni 1 ise bu sayılara aralarında asal sayılar denir. Her ikisi aralarında asal olan a,b,c pozitif tam sayı larının çarpımı 2100’dür. Buna göre, aşağıdakilerden h angisi bu üç sayıdan biri olamaz? A) 12 B) 24 C) 25 D) 28 E) 35 www.matematikkolay.net 2 2 Çözüm: 2100 ü asal çarpanlarına ayıralım: 2100 21.100 3.7.25.4 3.7.5 .2 dir. a,b ve c aralarında asal sayılar ise bu sayıların hiç birinde ortak bir asal çarpan olmamalıdır. Eğer sayılardan bir i E şıkkındaki gibi 35 olursa 5 ve 7 çarpanları kullanılmış olur. Ancak 2100 ün asal çarpanlarında 5, iki defa var dır. Bu se – beple başka bir sayıda 5, bir defa daha kullanı – lacaktır. Bu da aralarında asallığı bozacaktır. 4. x ve y doğal sayılar ve x 2 ile y 3 aralarında asaldır. x.y 3x 2y 17 olduğuna göre x.y çarpımı kaçtır? A) 18 B) 12 C) 16 D) 20 E) 24 1 11 Çözüm: x.y 3x 2y 17 (y parantezine alalım) y.(x 2) 3x 17 (her taraf tan 6 çıkaralım) y.(x 2) 3x 6 17 6 y.(x 2) 3x 6 11 y.(x 2) 3(x 2) 11 (x 2) parantezine alalım. (x 2)(y 3) 11 x 2 1 x 3 y 3 11 y 8 dir. x.y 3.8 24 buluruz. 8. 2x 1 ile y 1 aralarında asal sayılardır. 6x 5y 8 olduğuna göre, x.y çarpımı kaçtır? www.matematikkolay.net Çözüm: 6x 5y 8 6x 5y 8 0 6x 3 5y 5 0 3(2x 1) 5(y 1) 0 (2x 1) 5 3(2x 1) 5(y 1) (y 1) 3 (2x 1) ve (y 1) aralarında asal olduğuna göre; 2x 1 5 x 3 tür. y 1 3 y 2 dir. x.y 3.2 6 buluruz. 12. Aşağıda verilen şeklin karesel hücrelerine 1,2,3,4,5 ve 6 sayıları yerleştirilecektir. www.matematikkolay.net Yerleştirme işlemi aşağıdaki kurallara göre yapılacaktır. Her sayı bir hücrede yer alacaktır. Bir doğru parçasıyla birbirine bağlı olan karelerin içindeki sayılar aralarında asal olacaktır. Buna göre, a,d sıralı ikilisi aşağıdakilerden hangisidir? A) 4,2 B) 6,3 C) 5,3 D) 6,2 E) 2,4 www.matematikkolay.net Çözüm: Aralarında asal olan sayıların, tek ortak böleni 1 ol – malıdır. 1 2,3,4,5,6 ile aralarında asaldır. (5 bağlantı çizilebilir.) 2 1,3,5 ile aralarında asaldır. (3 bağlantı) 3 1,2,4 ,5 ile aralarında asaldır. (4 bağlantı) 4 1,3,5 ile aralarında asaldır. (3 bağlantı) 5 1,2,3,4,6 ile aralarında asaldır. (5 bağlantı) 6 1,5 ile aralarında asaldır. (2 bağlantı) Buna göre; a kutus u, 2 bağlantı çizilen tek kutudur. a 6 dır. d kutusu, 4 bağlantı çizilen tek kutudur. d 3 tür. (a,d) (6, 3) buluruz. 16. www.matematikkolay.net 5x 13 ile 2y 1 sayıları aralarında asal doğal sayılardır. 2x 5 2 3y 2 5 olduğuna göre, x.y çarpımı kaçtır? A) 3 B) 2 C) 1 D) 2 E) 3 Çözüm: 2x 5 2 10x 25 6y – 4 3y 2 5 10x 25 1 6y 4 1 10x 26 6y 3 2(5x 13) 3(2y 1) 5x 13 3 dir. 2y 1 2 5x 13 ve 2y 1 aralarında asal ise; 5x 13 3 5x 10 x -2 dir. 3 2y 1 2 2y 1 2 2y 3 y dir. 2 3 x.y -2 2 3 bulunur. 22. x y ile y z aralarında asal sayılardır. 7x 3y 4z olduğuna göre, x z kaçtır? A) 7 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net Çözüm: 7x 3y 4z iki tarafa da 4y ekleyelim. 7x 3y 4y 4y 4z 7x 7y 4y 4z 7(x y) 4(y z) x y 4 aralarında asal iseler; y z 7 x y 4 _ y z 7 dir. Taraf tarafa çıkarırsak; x z 3 buluruz. 28. www.matematikkolay.net x 2, y 5 aralarında asal sayılar olmak üzere, x y x 2 y 5 94 olduğuna göre x y farkı en çok kaçtır? A) 100 B) 96 C) 74 D) 48 E) 34 94 1 Çözüm: 94 94.1 çarpımı olarak düşünebiliriz. 94 ve 1 aralarında asaldır. (x 2) (y 5) 94 x 2 94 x 92 y 5 1 y 4 tür. Buna göre; x y 92 ( 4) 96 buluruz. 30. x y ile y z aralarında asal iki sayıdır. 9x 4y 5z olduğuna göre, z x farkı kaçtır? A) 3 B) 4 C) 5 D) 6 E) 7 Çözüm: 9x 4y 5z iki tarafa 5y ekleyelim. 9x 9y 5y 5z 9(x y) 5(y z) x y 5 dur. 5 ile 9 aralarında asal oduğundan; y z 9 x y 5 ve _ y z 9 dur. Taraf tarafa çıkarırsak; x z 4 tür. Buna göre; z x 4 buluruz. www.matematikkolay.net 31. 5a 4 ile 4b 1 aralarında asal ve 3a 4 2 4b 3 5 olduğuna göre, 5a 4b toplamı kaçtır? A) 6 B) 5 C) 4 D) 3 E) 2 8b 2 Çözüm: 3a 4 2 4b 3 5 15a 20 8b 6 3. 5a 4 8 8b 6 3. 5a 4 8b 6 8 3. 5a 4 2. 4b 1 5a 4 2 4b 1 3 5a 4 ile 4b 1 aralarında asal olduğundan; 5a 4 2 5a 2 dir. 4b 1 3 4b 4 tür. 5a 4b 2 4 6 bulunur. 32. m.n ve m 2n sayıları aralarında asal sayılardır. 6 m 3 2n n olduğuna göre, m 2n farkı kaçtır? A) 5 B) 4 C) 3 D) 2 E) 1 www.matematikkolay.net Çözüm: 6 m 3 2n n 6n 3m 2mn 2mn 3m 6n 2mn 3(m 2n) mn 3 Bunlar aralarında asal ise, m 2n 2 mn 3 ve m 2n 2 olmalıdır. Cevap: m 2n 2 buluruz. 34. x ve y pozitif tam sayılardır. 381381 x 183183 y olduğuna göre, x y ifadesinin en küçük değeri kaçtır? A) 54 B) 66 C) 127 D) 198 E) 201 Çözüm: x 381381 381.1000 381 381. (1000 1) y 183183 183.1000 183 183. (1000 1) x 381 y 127 183 61 127 61 x y 127 61 66 buluruz. www.matematikkolay.net 35. a b ile birbirinden farklı aralarında asal sayılar ise, 2 3 a b en az kaç olur? A) 13 B) 25 C) 53 D) 73 E) 85 www.matematikkolay.net Çözüm: 1 ile 1’den büyük tam sayılar, aralarında asaldır. b ‘ü 1 yaparsak, en küçük b’ yi elde ederiz. 3 b 1 b 1 b 9 dur. 3 Diğer sayıyı 1’den büyük, en küçük tam sayı yapalım. (Yani 2) a 2:00 AM 2 4 a 16 buluruz. O halde; a b 9 16 25 buluruz.


1. Soruda b şıkkı olamaz. 2100/24=87,5 yapar !!!
Uyarınız için teşekkürler. 21 yazılacağına 24 yazılmış. Şimdi hata düzeltildi.
9. Soruda işlem hatası var. 5a+4=2 5a= -4+2 olacağından 5a=-2 olmalıydı bu nedenle de sonuç 6 değil 2 olmalıydı.
Uyarınız için teşekkürler. Hata düzeltildi.